わかってない奴がわかったつもりで書き留める超準解析(その2) [数学]
【超準解析について生半可な知識しかない僕が、わかったつもりの内容をちょっとずつ書き留めていきます。不正確な内容や誤りもあることをご承知ください。】
(2) 実数体の超準モデル「超実数体」
実数の全体$\mathbb{R}$上には、順序関係$\le$、加法演算$+$、乗法演算 $\cdot$ と定数$0,1$が与えられ、それらに対してよく知られた一連の公理系が成立し、$\langle \mathbb{R}, \le, +, \cdot, 0,1 \rangle$ は実数体と呼ばれます(以下、実数体のことを簡単に$\mathbb{R}$で表します)。
ここで、2項演算は2変数関数であり、また定数は0変数関数であるので、第1回での一般的な議論が$\mathbb{R}$に対してもいえます。つまり、実数体を真に拡大する超準モデル $\langle {}^*\mathbb{R}, {}^*\le, {}^*+, {}^*\cdot, {}^*0,{}^*1 \rangle$ が存在します。これを超実数体と呼びます(これも以下簡単に${}^*\mathbb{R}$で表します)。さらに${}^*\mathbb{R}$の元を超実数と呼びます。
${}^*\le, {}^*+, {}^*\cdot$ はそれぞれ $\le, +, \cdot$ の拡大ですが、${}^*$は通常省略されます。また定数 ${}^*0,{}^*1$ はそれぞれ $0,1$ と一致しますのでこれらも${}^*$は必要ありません。
実数体の公理のうち、順序体の公理はすべて一階の論理式なので${}^*\mathbb{R}$でも成り立ちます。従って${}^*\mathbb{R}$は順序体です(なので${}^*\mathbb{R}$を超実数体と呼ぶことに何の問題もありません)。これに対し「実数体の完備性」と呼ばれる性質は一階の論理式で表現することができませんので、${}^*\mathbb{R}$で成り立つとはいえません。実際にも${}^*\mathbb{R}$では完備性が成り立たないことがこの後で証明されます。
では、超実数体${}^*\mathbb{R}$とは一体どんなものでしょうか。
${}^*\mathbb{R}$が$\mathbb{R}$を真に拡大するので、実数でない超実数が少なくとも1つ存在します。これを$a$とかくと、順序体の性質から次の2つのどちらかが成り立ちます。
① $a$の絶対値 $|a|$ はどんな実数よりも大きい($a$は無限大超実数)。
② $b < a < c$ となる実数$b,c$が存在する($a$は有限超実数)。
実は、①をみたす$a$と②をみたす$a$のどちらも存在します。それをこれから証明します。
まず、$a$が①をみたすとします。このとき逆数 $a^{-1} $が超実数として存在します。これは任意の正実数$b$に対して $0 < |a^{-1}| < b$ をみたすので、②をみたす実数でない超実数$a$が存在することになります。
任意の正実数$b$に対して $|a| < b$ をみたす$a$を無限小超実数と呼びます。$a$が0以外の無限小超実数ならば $a^{-1}$ は無限大超実数になり、その逆も成り立つことは明らかです。
次に、$a$が②をみたすとします。このとき、
\[
A = \{ x \in \mathbb{R} \mid x < a \} \\
B = \{ x \in \mathbb{R} \mid x > a \}
\]
とおくと、$\langle A,B \rangle$ は$\mathbb{R}$の「デデキントの切断」になるので、実数体の完備性より境界となる実数$d$が存在します。そして $e=a-d$ とおくと$e$は0以外の無限小超実数であることが容易にわかります。従ってその逆数 $e^{-1}$ は無限大超実数、すなわち①をみたす$a$が存在することになります。
以上で①をみたす$a$と②をみたす$a$のどちらも存在することが証明されました。つまり超実数は無限大超実数と有限超実数に分けられ、さらに有限超実数の特別なものとして無限小超実数がある、そして無限大超実数と0でない無限小超実数のいずれも存在する、ということになります。これらが無数に存在することも${}^*\mathbb{R}$が順序体であることから明らかです。
2つの超実数$a,b$について $a-b$ が無限小超実数であることを、「$a$と$b$は無限に近い」といい、
\[ a \approx b \]
と書きます。これは${}^*\mathbb{R}$上の同値関係です。0でない無限小超実数が無数に存在しますので、任意の超実数にはそれと無限に近い超実数が無数に存在することになります。
また、$a$が有限超実数ならば $b \approx a$ をみたす実数$b$が存在することが先ほど示されましたので、この$b$を $\mathrm{st}(a)$ とかき、$a$の標準部分と呼びます(唯一性は明らか)。つまり有限超実数は必ず標準部分をもつということになります。
以上のことから、超実数体${}^*\mathbb{R}$のイメージを図にすると、次のような感じになるでしょうか。
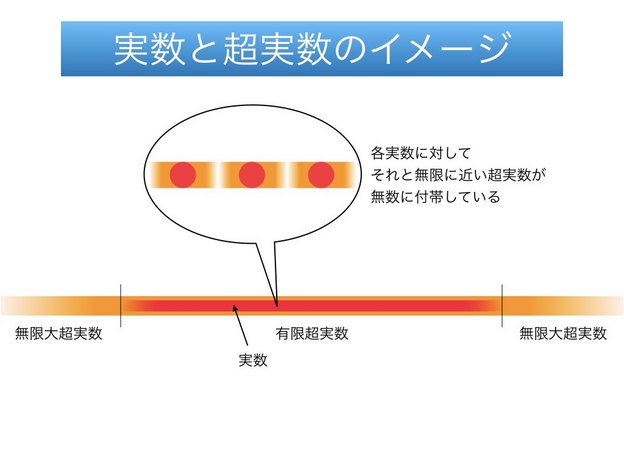
平たくいうと、超実数とは無限大や無限小を四則演算や大小比較のできる「数」として扱えるようにしたもの、といえます。
なお、$\mathbb{R}$で成り立つ完備性が${}^*\mathbb{R}$で成り立たないことは、有限超実数の全体が${}^*\mathbb{R}$において上限を持ち得ないことからわかります。そんなものがもしあれば、「最大の実数」の存在が示されるなど、すぐに矛盾が導かれてしまうからです。
(続く)(前記事)(目次)
(2) 実数体の超準モデル「超実数体」
実数の全体$\mathbb{R}$上には、順序関係$\le$、加法演算$+$、乗法演算 $\cdot$ と定数$0,1$が与えられ、それらに対してよく知られた一連の公理系が成立し、$\langle \mathbb{R}, \le, +, \cdot, 0,1 \rangle$ は実数体と呼ばれます(以下、実数体のことを簡単に$\mathbb{R}$で表します)。
ここで、2項演算は2変数関数であり、また定数は0変数関数であるので、第1回での一般的な議論が$\mathbb{R}$に対してもいえます。つまり、実数体を真に拡大する超準モデル $\langle {}^*\mathbb{R}, {}^*\le, {}^*+, {}^*\cdot, {}^*0,{}^*1 \rangle$ が存在します。これを超実数体と呼びます(これも以下簡単に${}^*\mathbb{R}$で表します)。さらに${}^*\mathbb{R}$の元を超実数と呼びます。
${}^*\le, {}^*+, {}^*\cdot$ はそれぞれ $\le, +, \cdot$ の拡大ですが、${}^*$は通常省略されます。また定数 ${}^*0,{}^*1$ はそれぞれ $0,1$ と一致しますのでこれらも${}^*$は必要ありません。
実数体の公理のうち、順序体の公理はすべて一階の論理式なので${}^*\mathbb{R}$でも成り立ちます。従って${}^*\mathbb{R}$は順序体です(なので${}^*\mathbb{R}$を超実数体と呼ぶことに何の問題もありません)。これに対し「実数体の完備性」と呼ばれる性質は一階の論理式で表現することができませんので、${}^*\mathbb{R}$で成り立つとはいえません。実際にも${}^*\mathbb{R}$では完備性が成り立たないことがこの後で証明されます。
では、超実数体${}^*\mathbb{R}$とは一体どんなものでしょうか。
${}^*\mathbb{R}$が$\mathbb{R}$を真に拡大するので、実数でない超実数が少なくとも1つ存在します。これを$a$とかくと、順序体の性質から次の2つのどちらかが成り立ちます。
① $a$の絶対値 $|a|$ はどんな実数よりも大きい($a$は無限大超実数)。
② $b < a < c$ となる実数$b,c$が存在する($a$は有限超実数)。
実は、①をみたす$a$と②をみたす$a$のどちらも存在します。それをこれから証明します。
まず、$a$が①をみたすとします。このとき逆数 $a^{-1} $が超実数として存在します。これは任意の正実数$b$に対して $0 < |a^{-1}| < b$ をみたすので、②をみたす実数でない超実数$a$が存在することになります。
任意の正実数$b$に対して $|a| < b$ をみたす$a$を無限小超実数と呼びます。$a$が0以外の無限小超実数ならば $a^{-1}$ は無限大超実数になり、その逆も成り立つことは明らかです。
次に、$a$が②をみたすとします。このとき、
\[
A = \{ x \in \mathbb{R} \mid x < a \} \\
B = \{ x \in \mathbb{R} \mid x > a \}
\]
とおくと、$\langle A,B \rangle$ は$\mathbb{R}$の「デデキントの切断」になるので、実数体の完備性より境界となる実数$d$が存在します。そして $e=a-d$ とおくと$e$は0以外の無限小超実数であることが容易にわかります。従ってその逆数 $e^{-1}$ は無限大超実数、すなわち①をみたす$a$が存在することになります。
以上で①をみたす$a$と②をみたす$a$のどちらも存在することが証明されました。つまり超実数は無限大超実数と有限超実数に分けられ、さらに有限超実数の特別なものとして無限小超実数がある、そして無限大超実数と0でない無限小超実数のいずれも存在する、ということになります。これらが無数に存在することも${}^*\mathbb{R}$が順序体であることから明らかです。
2つの超実数$a,b$について $a-b$ が無限小超実数であることを、「$a$と$b$は無限に近い」といい、
\[ a \approx b \]
と書きます。これは${}^*\mathbb{R}$上の同値関係です。0でない無限小超実数が無数に存在しますので、任意の超実数にはそれと無限に近い超実数が無数に存在することになります。
また、$a$が有限超実数ならば $b \approx a$ をみたす実数$b$が存在することが先ほど示されましたので、この$b$を $\mathrm{st}(a)$ とかき、$a$の標準部分と呼びます(唯一性は明らか)。つまり有限超実数は必ず標準部分をもつということになります。
以上のことから、超実数体${}^*\mathbb{R}$のイメージを図にすると、次のような感じになるでしょうか。

平たくいうと、超実数とは無限大や無限小を四則演算や大小比較のできる「数」として扱えるようにしたもの、といえます。
なお、$\mathbb{R}$で成り立つ完備性が${}^*\mathbb{R}$で成り立たないことは、有限超実数の全体が${}^*\mathbb{R}$において上限を持ち得ないことからわかります。そんなものがもしあれば、「最大の実数」の存在が示されるなど、すぐに矛盾が導かれてしまうからです。
(続く)(前記事)(目次)
2019-01-13 22:04
nice!(0)
コメント(0)




コメント 0