超フィルターによる全順序集合の拡大 [数学]
【この記事は 日曜数学 Advent Calendar 2021 の、12月12日用として書きました。】
「超フィルター」については、知っている人はよく知っていると思います(知らない方はWikipediaの記事などを参照してください)。コンパクト性の特徴付けや超準解析に使われるなど、色々と面白い性質を持っています。
この超フィルターを使って、全順序集合を拡大することができます。この辺りの話は探せばどこかに論文や記事があると思いますが、練習問題のつもりで自分でやってみたところ、予想に反して何やら奇妙な集合ができあがってきましたので、本記事ではそれを紹介します。
0.予備知識
まず、本記事で用いるフィルターに関する予備知識を列記します。
$X$ を空でない集合とすると、$X$ の部分集合の族 $\mathbf{F} \, ( \neq \emptyset )$ が $X$ の冪集合上のフィルター(本記事では単に $X$ 上のフィルターと言います)であるとは、次の3つの条件を満たすことを言います。
(1) $\emptyset \notin \mathbf{F}$
(2) $A, B \in \mathbf{F} \to A \cap B \in \mathbf{F}$
(3) $A \in \mathbf{F} \land A \subseteq B \subseteq X \to B \in \mathbf{F}$
(1)と(2)から、フィルターから有限個の元をどう取っても、それらの共通部分は空にならないことがわかります。この性質を有限交差性と言います。逆に、$X$ の部分集合の族が有限交差性を持つならば、それらを含む $X$ 上のフィルターが存在します。
ツォルンの補題を使うと、任意のフィルターに対し、それを含む極大フィルターの存在が証明できます。極大フィルターは超フィルターとも呼ばれます。$X$ 上のフィルター $\mathbf{F}$ が超フィルターであることと、次の性質とは同値です。
(4) $A \subseteq X \to A \in \mathbf{F} \lor X \setminus A \in \mathbf{F}$
$X$ の任意の元 $x$ に対し、$x$ を元に持つ $X$ の部分集合の全体は、超フィルターになります。これを $x$ が生成する単項フィルターと呼び、$\uparrow x$ と書きます。$X$ が有限集合ならば $X$ 上の超フィルターは必ず単項フィルターですが、$X$ が無限集合ならば単項フィルターにならない超フィルター(非単項超フィルター)が存在します。
非単項超フィルターは実体がイメージしにくく、存在することはわかっても具体的にビシッと記述することはできませんが、それだけに深掘りすると面白いです。しかし本記事で用いる予備知識としてはここまであれば十分です。
1.超フィルター間に擬順序関係を定める
$(X, \le)$ を全順序集合とします。例えば有理数の順序集合 $(\mathbb{Q}, \le)$ がその一例です。
$X$ 上の超フィルターの全体を $\mathrm{U}(X)$ とし、その元 $\mathbf{A}, \mathbf{B}$ に対して次によって関係 $\preceq$ を定めます。
\begin{equation*}
\mathbf{A} \preceq \mathbf{B} \quad \Leftrightarrow \quad \forall A \in \mathbf{A} \, \forall B \in \mathbf{B} \, \exists a \in A \, \exists b \in B \, (a \le b)
\end{equation*}
つまり「超フィルター $\mathbf{A}$ と $\mathbf{B}$ からそれぞれどのように( $X$ の部分集合である)元 $A,B$ を取っても、$B$ が $A$ より完全に下になることはない」という関係を $\mathbf{A} \preceq \mathbf{B}$ と定めるわけです。以下見やすさのために、$X$ の部分集合 $A,B$ について「$B$ が $A$ より完全に下になる」という条件を $B < A$ すなわち、
\begin{equation*}
B < A \quad \Leftrightarrow \quad \forall a \in A \, \forall b \in B \, (b < a)
\end{equation*}
のように略記することにします。こうすると、
\begin{equation*}
\mathbf{A} \preceq \mathbf{B} \quad \Leftrightarrow \quad \forall A \in \mathbf{A} \, \forall B \in \mathbf{B} \, \lnot(B < A)
\end{equation*}
となります。イメージ図にすると次の感じです。
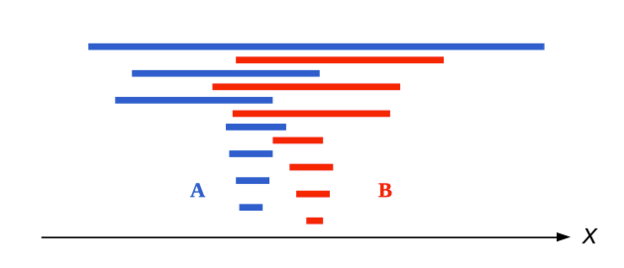
この関係 $\preceq$ は $\mathrm{U}(X)$ 上の全擬順序関係になります。証明は次のとおりです。
[反射律]フィルターの有限交差性から $\mathbf{A} \preceq \mathbf{A}$ は明らか。
[推移律]$\mathbf{A},\mathbf{B},\mathbf{C} \in \mathrm{U}(X), \ \mathbf{A} \preceq \mathbf{B} \land \mathbf{B} \preceq \mathbf{C} \land \lnot (\mathbf{A} \preceq \mathbf{C})$ と仮定して矛盾を導く。このときある $A \in \mathbf{A}, C \in \mathbf{C}$ が存在して $C < A$ となる。そして任意に $B \in \mathbf{B}$ をとると、
\begin{equation*}
\lnot(B < A) \land \lnot(C < B)
\end{equation*}
が成立する。そこで、
\begin{equation*}
C' = \{ \, x \in X \, \mid \, \exists c \in C \, (x \le c) \, \}
\end{equation*}
と定めると、$C' < A$ だから $C' \notin \mathbf{B}$ であり、かつ $\mathbf{B} \cup \{ C' \}$ は有限交差性を持つ。従って $\mathbf{B} \cup \{ C' \}$ を含むフィルターが存在し、それは $\mathbf{B}$ を真に拡張する。このことは $\mathbf{B}$ が超フィルター(=極大フィルター)であることと矛盾する。
[比較可能律]$\mathbf{A},\mathbf{B} \in \mathrm{U}(X), \ \lnot(\mathbf{A} \preceq \mathbf{B}) \land \lnot(\mathbf{B} \preceq \mathbf{A})$ と仮定して矛盾を導く。このときある $A_1,A_2 \in \mathbf{A}$ と $B_1,B_2 \in \mathbf{B}$ が存在して $B_1 < A_1 \land A_2 < B_2$ となる。フィルターの有限交差性から $a \in A_1 \cap A_2, b \in B_1 \cap B_2$ となる $a,b$ がとれるが、これに対して $b < a \land a < b$ となるから矛盾を生じる。
以上で関係 $\preceq$ が $\mathrm{U}(X)$ 上の全擬順序関係になることが証明できました。推移律の証明に超フィルターであることを使用しています。
2.同値類によって全順序集合を構成する
全擬順序集合 $(\mathrm{U}(X), \preceq)$ から、一般論によって全順序集合を構成することができます。
$\mathrm{U}(X)$ 上に関係 $\sim$ を、
\begin{equation*}
\mathbf{A} \sim \mathbf{B} \quad \Leftrightarrow \quad \mathbf{A} \preceq \mathbf{B} \land \mathbf{B} \preceq \mathbf{A}
\end{equation*}
によって定めると、$\sim$ は同値関係です。そこで、商集合 $\mathrm{U}(X) / \sim$ を $\widehat{X}$ とおくと、$\widehat{X}$ 上に自然な順序関係 $\le$ が定まり、$(\widehat{X}, \le)$ は全順序集合になります。以下、$\mathbf{A} \in \mathrm{U}(X)$ を代表元とする $\widehat{X}$ の元を $[ \mathbf{A} ]$ と書きます。
$a \in X$ に対し、$a$ で生成される $X$ 上の単項フィルター $\uparrow a$ は超フィルターですから、$a$ と $[ \uparrow a ]$ を同一視することによって、$X$ を順序を保って $\widehat{X}$ に埋め込むことができます。
これで全順序集合 $X$ を超フィルターを使って全順序集合 $\widehat{X}$ に拡大することができました。
3.何ができあがったのか?
さて、問題はこのようにして作られた全順序集合 $\widehat{X}$ がなにものかということです。
はじめ、$\widehat{X}$ は $X$ の順序完備化になるとばかり思っていました。ところが、完備化の条件である「 $X$ は $\widehat{X}$ において稠密」という命題が、$X$ に自己稠密という条件をつけても、どうにも証明できません。よく考えると次のような反例が存在します。
$X$ を有理数の全体 $\mathbb{Q}$ とし、上の方法で $\widehat{\mathbb{Q}}$ を構成します。無理数 $\gamma$ をひとつとると、$\mathbb{Q}$ の区間 $[x, \gamma)$ の全体は有限交差性を持つので、それらを含む超フィルター $\mathbf{C}_-$ が作れます。同様に $\mathbb{Q}$ の区間 $(\gamma, x]$ の全体は有限交差性を持つので、それらを含む超フィルター $\mathbf{C}_+$ が作れます(少し記号の濫用をしていますが、解釈できると思います)。このとき明らかに $\lnot(\mathbf{C}_+ \preceq \mathbf{C}_-)$ なので $\gamma_- = [\mathbf{C}_-], \ \gamma_+ = [\mathbf{C}_+]$ とおくと、$\gamma_- < \gamma_+$ になります。そして明らかに、$a < \gamma$ なる有理数 $a$ と $\gamma < b$ なる有理数 $b$ に対して、$\widehat{\mathbb{Q}}$ 上で $a < \gamma_- < \gamma_+ < b$ です。つまり $\gamma_-$ と $\gamma_+$ の間には有理数は存在せず、$\mathbb{Q}$ は $\widehat{\mathbb{Q}}$ において稠密ではありません。
$\mathbb{Q}$ を順序完備化すると実数の順序空間 $\mathbb{R}$ が得られますが、この方法で得られた $\widehat{\mathbb{Q}}$ はそれ以上の何か、少なくとも各無理数に対して「下側の無理数」と「上側の無理数」の2つが存在する空間になっています。
さらに、もし $\gamma$ が有理数ならば、同様に作られた超フィルター $\mathbf{C}_+, \mathbf{C}_-$ のほかに単項フィルター $\uparrow \gamma$ が存在して $[\mathbf{C}_-] < [\uparrow \gamma] < [\mathbf{C}_+]$ すなわち $\gamma_- < \gamma < \gamma_+$ となるので、各有理数に対しては「下側の有理数」と「真ん中の有理数」と「上側の有理数」の3つが存在します。
一方で、証明は少し長いので省略しますが、$\widehat{X}$ は順序完備にはなります。すなわち $\widehat{X}$ のデデキント切断 $(A, B)$ には必ず $\max{A}$ または $\min{B}$ のどちらかが存在します。このとき $\max{A}$ と $\min{B}$ の両方が存在し得ることは、先ほどの反例からもわかります。
$X$ が順序群のときに、群演算を $\widehat{X}$ に拡大することができるのか、$X$ が半順序集合のときはどうなるのかなど興味は尽きませんが、まだ自分の頭の中で整理できていませんので、今回はここまでにしておきます。
(続く)
「超フィルター」については、知っている人はよく知っていると思います(知らない方はWikipediaの記事などを参照してください)。コンパクト性の特徴付けや超準解析に使われるなど、色々と面白い性質を持っています。
この超フィルターを使って、全順序集合を拡大することができます。この辺りの話は探せばどこかに論文や記事があると思いますが、練習問題のつもりで自分でやってみたところ、予想に反して何やら奇妙な集合ができあがってきましたので、本記事ではそれを紹介します。
0.予備知識
まず、本記事で用いるフィルターに関する予備知識を列記します。
$X$ を空でない集合とすると、$X$ の部分集合の族 $\mathbf{F} \, ( \neq \emptyset )$ が $X$ の冪集合上のフィルター(本記事では単に $X$ 上のフィルターと言います)であるとは、次の3つの条件を満たすことを言います。
(1) $\emptyset \notin \mathbf{F}$
(2) $A, B \in \mathbf{F} \to A \cap B \in \mathbf{F}$
(3) $A \in \mathbf{F} \land A \subseteq B \subseteq X \to B \in \mathbf{F}$
(1)と(2)から、フィルターから有限個の元をどう取っても、それらの共通部分は空にならないことがわかります。この性質を有限交差性と言います。逆に、$X$ の部分集合の族が有限交差性を持つならば、それらを含む $X$ 上のフィルターが存在します。
ツォルンの補題を使うと、任意のフィルターに対し、それを含む極大フィルターの存在が証明できます。極大フィルターは超フィルターとも呼ばれます。$X$ 上のフィルター $\mathbf{F}$ が超フィルターであることと、次の性質とは同値です。
(4) $A \subseteq X \to A \in \mathbf{F} \lor X \setminus A \in \mathbf{F}$
$X$ の任意の元 $x$ に対し、$x$ を元に持つ $X$ の部分集合の全体は、超フィルターになります。これを $x$ が生成する単項フィルターと呼び、$\uparrow x$ と書きます。$X$ が有限集合ならば $X$ 上の超フィルターは必ず単項フィルターですが、$X$ が無限集合ならば単項フィルターにならない超フィルター(非単項超フィルター)が存在します。
非単項超フィルターは実体がイメージしにくく、存在することはわかっても具体的にビシッと記述することはできませんが、それだけに深掘りすると面白いです。しかし本記事で用いる予備知識としてはここまであれば十分です。
1.超フィルター間に擬順序関係を定める
$(X, \le)$ を全順序集合とします。例えば有理数の順序集合 $(\mathbb{Q}, \le)$ がその一例です。
$X$ 上の超フィルターの全体を $\mathrm{U}(X)$ とし、その元 $\mathbf{A}, \mathbf{B}$ に対して次によって関係 $\preceq$ を定めます。
\begin{equation*}
\mathbf{A} \preceq \mathbf{B} \quad \Leftrightarrow \quad \forall A \in \mathbf{A} \, \forall B \in \mathbf{B} \, \exists a \in A \, \exists b \in B \, (a \le b)
\end{equation*}
つまり「超フィルター $\mathbf{A}$ と $\mathbf{B}$ からそれぞれどのように( $X$ の部分集合である)元 $A,B$ を取っても、$B$ が $A$ より完全に下になることはない」という関係を $\mathbf{A} \preceq \mathbf{B}$ と定めるわけです。以下見やすさのために、$X$ の部分集合 $A,B$ について「$B$ が $A$ より完全に下になる」という条件を $B < A$ すなわち、
\begin{equation*}
B < A \quad \Leftrightarrow \quad \forall a \in A \, \forall b \in B \, (b < a)
\end{equation*}
のように略記することにします。こうすると、
\begin{equation*}
\mathbf{A} \preceq \mathbf{B} \quad \Leftrightarrow \quad \forall A \in \mathbf{A} \, \forall B \in \mathbf{B} \, \lnot(B < A)
\end{equation*}
となります。イメージ図にすると次の感じです。

この関係 $\preceq$ は $\mathrm{U}(X)$ 上の全擬順序関係になります。証明は次のとおりです。
[反射律]フィルターの有限交差性から $\mathbf{A} \preceq \mathbf{A}$ は明らか。
[推移律]$\mathbf{A},\mathbf{B},\mathbf{C} \in \mathrm{U}(X), \ \mathbf{A} \preceq \mathbf{B} \land \mathbf{B} \preceq \mathbf{C} \land \lnot (\mathbf{A} \preceq \mathbf{C})$ と仮定して矛盾を導く。このときある $A \in \mathbf{A}, C \in \mathbf{C}$ が存在して $C < A$ となる。そして任意に $B \in \mathbf{B}$ をとると、
\begin{equation*}
\lnot(B < A) \land \lnot(C < B)
\end{equation*}
が成立する。そこで、
\begin{equation*}
C' = \{ \, x \in X \, \mid \, \exists c \in C \, (x \le c) \, \}
\end{equation*}
と定めると、$C' < A$ だから $C' \notin \mathbf{B}$ であり、かつ $\mathbf{B} \cup \{ C' \}$ は有限交差性を持つ。従って $\mathbf{B} \cup \{ C' \}$ を含むフィルターが存在し、それは $\mathbf{B}$ を真に拡張する。このことは $\mathbf{B}$ が超フィルター(=極大フィルター)であることと矛盾する。
[比較可能律]$\mathbf{A},\mathbf{B} \in \mathrm{U}(X), \ \lnot(\mathbf{A} \preceq \mathbf{B}) \land \lnot(\mathbf{B} \preceq \mathbf{A})$ と仮定して矛盾を導く。このときある $A_1,A_2 \in \mathbf{A}$ と $B_1,B_2 \in \mathbf{B}$ が存在して $B_1 < A_1 \land A_2 < B_2$ となる。フィルターの有限交差性から $a \in A_1 \cap A_2, b \in B_1 \cap B_2$ となる $a,b$ がとれるが、これに対して $b < a \land a < b$ となるから矛盾を生じる。
以上で関係 $\preceq$ が $\mathrm{U}(X)$ 上の全擬順序関係になることが証明できました。推移律の証明に超フィルターであることを使用しています。
2.同値類によって全順序集合を構成する
全擬順序集合 $(\mathrm{U}(X), \preceq)$ から、一般論によって全順序集合を構成することができます。
$\mathrm{U}(X)$ 上に関係 $\sim$ を、
\begin{equation*}
\mathbf{A} \sim \mathbf{B} \quad \Leftrightarrow \quad \mathbf{A} \preceq \mathbf{B} \land \mathbf{B} \preceq \mathbf{A}
\end{equation*}
によって定めると、$\sim$ は同値関係です。そこで、商集合 $\mathrm{U}(X) / \sim$ を $\widehat{X}$ とおくと、$\widehat{X}$ 上に自然な順序関係 $\le$ が定まり、$(\widehat{X}, \le)$ は全順序集合になります。以下、$\mathbf{A} \in \mathrm{U}(X)$ を代表元とする $\widehat{X}$ の元を $[ \mathbf{A} ]$ と書きます。
$a \in X$ に対し、$a$ で生成される $X$ 上の単項フィルター $\uparrow a$ は超フィルターですから、$a$ と $[ \uparrow a ]$ を同一視することによって、$X$ を順序を保って $\widehat{X}$ に埋め込むことができます。
これで全順序集合 $X$ を超フィルターを使って全順序集合 $\widehat{X}$ に拡大することができました。
3.何ができあがったのか?
さて、問題はこのようにして作られた全順序集合 $\widehat{X}$ がなにものかということです。
はじめ、$\widehat{X}$ は $X$ の順序完備化になるとばかり思っていました。ところが、完備化の条件である「 $X$ は $\widehat{X}$ において稠密」という命題が、$X$ に自己稠密という条件をつけても、どうにも証明できません。よく考えると次のような反例が存在します。
$X$ を有理数の全体 $\mathbb{Q}$ とし、上の方法で $\widehat{\mathbb{Q}}$ を構成します。無理数 $\gamma$ をひとつとると、$\mathbb{Q}$ の区間 $[x, \gamma)$ の全体は有限交差性を持つので、それらを含む超フィルター $\mathbf{C}_-$ が作れます。同様に $\mathbb{Q}$ の区間 $(\gamma, x]$ の全体は有限交差性を持つので、それらを含む超フィルター $\mathbf{C}_+$ が作れます(少し記号の濫用をしていますが、解釈できると思います)。このとき明らかに $\lnot(\mathbf{C}_+ \preceq \mathbf{C}_-)$ なので $\gamma_- = [\mathbf{C}_-], \ \gamma_+ = [\mathbf{C}_+]$ とおくと、$\gamma_- < \gamma_+$ になります。そして明らかに、$a < \gamma$ なる有理数 $a$ と $\gamma < b$ なる有理数 $b$ に対して、$\widehat{\mathbb{Q}}$ 上で $a < \gamma_- < \gamma_+ < b$ です。つまり $\gamma_-$ と $\gamma_+$ の間には有理数は存在せず、$\mathbb{Q}$ は $\widehat{\mathbb{Q}}$ において稠密ではありません。
$\mathbb{Q}$ を順序完備化すると実数の順序空間 $\mathbb{R}$ が得られますが、この方法で得られた $\widehat{\mathbb{Q}}$ はそれ以上の何か、少なくとも各無理数に対して「下側の無理数」と「上側の無理数」の2つが存在する空間になっています。
さらに、もし $\gamma$ が有理数ならば、同様に作られた超フィルター $\mathbf{C}_+, \mathbf{C}_-$ のほかに単項フィルター $\uparrow \gamma$ が存在して $[\mathbf{C}_-] < [\uparrow \gamma] < [\mathbf{C}_+]$ すなわち $\gamma_- < \gamma < \gamma_+$ となるので、各有理数に対しては「下側の有理数」と「真ん中の有理数」と「上側の有理数」の3つが存在します。
一方で、証明は少し長いので省略しますが、$\widehat{X}$ は順序完備にはなります。すなわち $\widehat{X}$ のデデキント切断 $(A, B)$ には必ず $\max{A}$ または $\min{B}$ のどちらかが存在します。このとき $\max{A}$ と $\min{B}$ の両方が存在し得ることは、先ほどの反例からもわかります。
$X$ が順序群のときに、群演算を $\widehat{X}$ に拡大することができるのか、$X$ が半順序集合のときはどうなるのかなど興味は尽きませんが、まだ自分の頭の中で整理できていませんので、今回はここまでにしておきます。
(続く)




コメント 0