ロピタルの定理の超準解析での証明例 [数学]
前回の記事に続いて、超準解析を使った証明例です。
ロピタルの定理の ∞/∞ バージョンを証明します。Wikipedia に載っている証明例をみるとわかるように、普通は結構面倒なテクニックを使って証明されているようです。
【定理】
$f,g$ は $\mathbb{R}$ の区間 $[a, +\infty)$ 上で定義された微分可能な実関数で、
\[ \lim_{x \to +\infty} f(x) = \lim_{x \to +\infty} g(x) = +\infty \]
をみたし、かつ $x \in [a, +\infty)$ で $g'(x) \neq 0$ とする。このとき $\displaystyle \lim_{x \to +\infty} \frac{f'(x)}{g'(x)} = L$ が存在するならば $\displaystyle \lim_{x \to +\infty} \frac{f(x)}{g(x)} = L$ である。
(証明)
$f,g$ の ${}^*\mathbb{R}$ への自然延長を ${}^*f,{}^*g$ とする。任意に正の無限大超実数 $x$ をとる。仮定より ${}^*f(x),{}^*g(x)$ は正の無限大である。このとき、
\[ y < x \land {}^*f(y) \le \sqrt{{}^*f(x)} \land {}^*g(y) \le \sqrt{{}^*g(x)} \]
をみたす正の無限大超実数 $y$ がとれる。なぜなら、$f$ が連続だから中間値の定理と移行原理によって、
\[ a < y_1 < x \land {}^*f(y_1)=\sqrt{{}^*f(x)} \]
をみたす最小の $y_1$ が存在し、$\displaystyle \sqrt{{}^*f(x)}$ が正の無限大だから $y_1$ も正の無限大。同様に
\[ a < y_2 < x \land {}^*g(y_2)=\sqrt{{}^*g(x)} \]
をみたす最小の $y_2$ が存在するから、$y=\textrm{min}\{ \, y_1,y_2 \, \}$ とすると $y$ は所要のものになる。そして
\[ 0 < \frac{{}^*f(y)}{{}^*f(x)} \le \frac{1}{\sqrt{{}^*f(x)}} \approx 0 \]
より $\displaystyle \frac{{}^*f(y)}{{}^*f(x)} \approx 0$ となり、同様に $\displaystyle \frac{{}^*g(y)}{{}^*g(x)} \approx 0$ となる。一方、コーシーの平均値の定理と移行原理によって、
\[ y < c < x \land \frac{{}^*f(x)-{}^*f(y)}{{}^*g(x)-{}^*g(y)}=\frac{{}^*f'(c)}{{}^*g'(c)} \]
をみたす正の無限大超実数 $c$ が存在し、これに対して
\[ \frac{{}^*f(x)}{{}^*g(x)} \cdot \frac{1-{}^*f(y)/{}^*f(x)}{1-{}^*g(y)/{}^*g(x)} = \frac{{}^*f'(c)}{{}^*g'(c)} \]
となるから、両辺の標準部分をとると、
\[ \mathrm{st} \left( \frac{{}^*f(x)}{{}^*g(x)} \right) = \mathrm{st} \left( \frac{{}^*f'(c)}{{}^*g'(c)} \right) = L \]
$x$ は任意の正の無限大超実数だから $\displaystyle \lim_{x \to +\infty} \frac{f(x)}{g(x)} = L$ が得られる。(証明終)
ここでも無限大超実数の平方根が現れました。このように様々な大きさの無限大が自由に作れるのが超準解析の便利なところです。普通の証明よりもう少し直感的に理解しやすいのではないでしょうか。
ロピタルの定理の ∞/∞ バージョンを証明します。Wikipedia に載っている証明例をみるとわかるように、普通は結構面倒なテクニックを使って証明されているようです。
【定理】
$f,g$ は $\mathbb{R}$ の区間 $[a, +\infty)$ 上で定義された微分可能な実関数で、
\[ \lim_{x \to +\infty} f(x) = \lim_{x \to +\infty} g(x) = +\infty \]
をみたし、かつ $x \in [a, +\infty)$ で $g'(x) \neq 0$ とする。このとき $\displaystyle \lim_{x \to +\infty} \frac{f'(x)}{g'(x)} = L$ が存在するならば $\displaystyle \lim_{x \to +\infty} \frac{f(x)}{g(x)} = L$ である。
(証明)
$f,g$ の ${}^*\mathbb{R}$ への自然延長を ${}^*f,{}^*g$ とする。任意に正の無限大超実数 $x$ をとる。仮定より ${}^*f(x),{}^*g(x)$ は正の無限大である。このとき、
\[ y < x \land {}^*f(y) \le \sqrt{{}^*f(x)} \land {}^*g(y) \le \sqrt{{}^*g(x)} \]
をみたす正の無限大超実数 $y$ がとれる。なぜなら、$f$ が連続だから中間値の定理と移行原理によって、
\[ a < y_1 < x \land {}^*f(y_1)=\sqrt{{}^*f(x)} \]
をみたす最小の $y_1$ が存在し、$\displaystyle \sqrt{{}^*f(x)}$ が正の無限大だから $y_1$ も正の無限大。同様に
\[ a < y_2 < x \land {}^*g(y_2)=\sqrt{{}^*g(x)} \]
をみたす最小の $y_2$ が存在するから、$y=\textrm{min}\{ \, y_1,y_2 \, \}$ とすると $y$ は所要のものになる。そして
\[ 0 < \frac{{}^*f(y)}{{}^*f(x)} \le \frac{1}{\sqrt{{}^*f(x)}} \approx 0 \]
より $\displaystyle \frac{{}^*f(y)}{{}^*f(x)} \approx 0$ となり、同様に $\displaystyle \frac{{}^*g(y)}{{}^*g(x)} \approx 0$ となる。一方、コーシーの平均値の定理と移行原理によって、
\[ y < c < x \land \frac{{}^*f(x)-{}^*f(y)}{{}^*g(x)-{}^*g(y)}=\frac{{}^*f'(c)}{{}^*g'(c)} \]
をみたす正の無限大超実数 $c$ が存在し、これに対して
\[ \frac{{}^*f(x)}{{}^*g(x)} \cdot \frac{1-{}^*f(y)/{}^*f(x)}{1-{}^*g(y)/{}^*g(x)} = \frac{{}^*f'(c)}{{}^*g'(c)} \]
となるから、両辺の標準部分をとると、
\[ \mathrm{st} \left( \frac{{}^*f(x)}{{}^*g(x)} \right) = \mathrm{st} \left( \frac{{}^*f'(c)}{{}^*g'(c)} \right) = L \]
$x$ は任意の正の無限大超実数だから $\displaystyle \lim_{x \to +\infty} \frac{f(x)}{g(x)} = L$ が得られる。(証明終)
ここでも無限大超実数の平方根が現れました。このように様々な大きさの無限大が自由に作れるのが超準解析の便利なところです。普通の証明よりもう少し直感的に理解しやすいのではないでしょうか。
チェザロ平均の収束の超準解析での証明例 [数学]
超準解析を使った簡単な証明例を紹介します。
個人的には、この短い証明の中に超準解析の入口としての面白さが凝縮されているような気がしています。
【定理】
実数列 $\{a_n\}$ が実数 $\alpha$ に収束するとき、チェザロ平均と呼ばれる
\[c_n = \sum_{k=1}^n \frac{a_k}{n} = \frac{a_1 + a_2 + \cdots + a_n}{n} \]
で定まる実数列 $\{c_n\}$ も $\alpha$ に収束する。
(証明)
$\{a_n\}, \, \{c_n\}$ とも超準拡大によって添字を無限大超自然数の範囲まで広げておく。$n$ が任意にとった無限大超自然数のとき $c_n \approx \alpha$(無限に近いこと)を示せばよい。$m<\sqrt{n}$ をみたす無限大超自然数 $m$ がとれる。 $\{a_n\}$ は有界だから $\{ \left| a_n - \alpha \right| \}$ の上界となる実数 $M$ がとれ、また $\displaystyle \mu = \max_{m+1 \le k \le n} \left| a_k - \alpha \right|$ が存在し、 $\{a_n\}$ が$\alpha$ に収束するからこの $\mu$ は無限小である。従って、
\[\left| c_n - \alpha \right| = \left| \sum_{k=1}^n \frac{a_k - \alpha}{n} \right| \le \sum_{k=1}^m \frac{\left| a_k - \alpha \right|}{n} + \sum_{k=m+1}^n \frac{\left| a_k - \alpha \right|}{n} \le \frac{Mm}{n} + \frac{\mu (n-m)}{n} < \frac{M}{\sqrt{n}} + \mu \approx 0 \]
より $c_n \approx \alpha$ が得られる。(証明終)
この証明に使われている超準解析らしい面白ポイントは次のものが挙げられるでしょう。
①無限大にも(正ならば)平方根が存在し、それもまた無限大であること。
②あたかも有限個の和と同じように「無限大超自然数個の和」が扱えること。
③数列の有限個の範囲で最大値が存在するのと同じように、無限大超自然数の範囲でも最大値が存在すること。
これらはみんな、実数の世界で成立する性質を移行原理によって超実数の世界に持っていったものなので、同様に成立するわけです。
個人的には、この短い証明の中に超準解析の入口としての面白さが凝縮されているような気がしています。
【定理】
実数列 $\{a_n\}$ が実数 $\alpha$ に収束するとき、チェザロ平均と呼ばれる
\[c_n = \sum_{k=1}^n \frac{a_k}{n} = \frac{a_1 + a_2 + \cdots + a_n}{n} \]
で定まる実数列 $\{c_n\}$ も $\alpha$ に収束する。
(証明)
$\{a_n\}, \, \{c_n\}$ とも超準拡大によって添字を無限大超自然数の範囲まで広げておく。$n$ が任意にとった無限大超自然数のとき $c_n \approx \alpha$(無限に近いこと)を示せばよい。$m<\sqrt{n}$ をみたす無限大超自然数 $m$ がとれる。 $\{a_n\}$ は有界だから $\{ \left| a_n - \alpha \right| \}$ の上界となる実数 $M$ がとれ、また $\displaystyle \mu = \max_{m+1 \le k \le n} \left| a_k - \alpha \right|$ が存在し、 $\{a_n\}$ が$\alpha$ に収束するからこの $\mu$ は無限小である。従って、
\[\left| c_n - \alpha \right| = \left| \sum_{k=1}^n \frac{a_k - \alpha}{n} \right| \le \sum_{k=1}^m \frac{\left| a_k - \alpha \right|}{n} + \sum_{k=m+1}^n \frac{\left| a_k - \alpha \right|}{n} \le \frac{Mm}{n} + \frac{\mu (n-m)}{n} < \frac{M}{\sqrt{n}} + \mu \approx 0 \]
より $c_n \approx \alpha$ が得られる。(証明終)
この証明に使われている超準解析らしい面白ポイントは次のものが挙げられるでしょう。
①無限大にも(正ならば)平方根が存在し、それもまた無限大であること。
②あたかも有限個の和と同じように「無限大超自然数個の和」が扱えること。
③数列の有限個の範囲で最大値が存在するのと同じように、無限大超自然数の範囲でも最大値が存在すること。
これらはみんな、実数の世界で成立する性質を移行原理によって超実数の世界に持っていったものなので、同様に成立するわけです。
佐久から諏訪へ 中山道と白樺湖・霧ヶ峰を結ぶ路線バスの旅 [バス]
仕事の夏休みを使って、路線バス旅の遠征をしてきました。
長野県の佐久平駅から上諏訪駅まで、白樺湖、霧ヶ峰という景色のよいリゾート地帯を通過します。
後から調べてわかったのですが、このルートはかつての中山道に並行しており、長和町を経由する国道142号線がほぼ中山道を辿ったルートになっています。中山道を忠実に辿る路線バスの旅というのもちょっと惹かれましたが、江戸時代も難所だった和田峠(長和町〜下諏訪町間)が現在も難所で、ここを通過する路線がなく歩くのもちょっとしんどい。今回はバスだけで乗り継げる白樺湖経由のルートにしました。
大阪を早朝に出発すると、佐久平駅へは昼前に着きます。北陸新幹線は便利です。


佐久平駅から千曲バスで立科町役場前まで行きます。このバスは立科町役場前行なのに、バス乗り場には時刻表を含めて「望月・芦田方面行」としか書かれてないので戸惑いました。地域名で行先を書くのは部外者にはわかりにくいです。

路線名が「中仙道線」とあるとおり、ほぼ中山道に沿ったルートを走ります。始発の岩村田、途中の塩名田、八幡、望月、終点の芦田はどれも旧宿場町です。



立科町役場前での乗り継ぎの時間を使って、芦田宿跡を散策しました。本陣跡やちょっとした案内所がありましたが、観光地として賑わう様子はありません。


ここから立科町営の「たてしなスマイル交通」で東白樺湖に向かいます。地図を見ると芦田から白樺湖の東半分まで狭い回廊のように立科町域が伸びており、その間をこのバスが結んでいるのです。

雨が降ってきましたが、緑深い高原地帯に入り、途中蓼科牧場や女神湖を横に見ながら景色のよい道を走ります。白樺湖に近づくにつれて観光客がパラパラと乗ってきました。



終点の東白樺湖のあたりはすっかりレジャーランドの様相で、盆休みの真っ只中なので車や人でごった返していました。


ここからアルピコ交通のバスで上諏訪駅まで行きます。この路線は茅野駅から白樺湖、車山高原、霧ヶ峰を回って上諏訪駅までを結ぶ、なかなかのロングラン路線です。

曇り空で、途中から激しく雨が降ってきましたが、霧ヶ峰高原はやはりなかなかの絶景でした。贅沢な路線バスです。





諏訪盆地へ下って行きます。諏訪湖をチラッと見て、上諏訪駅に到着です。



佐久から諏訪という鉄道が直接結んでいない2地点を路線バスで走破し、しかも雄大な景色も堪能できるという、ちょっと贅沢な路線バス旅でした。
長野県の佐久平駅から上諏訪駅まで、白樺湖、霧ヶ峰という景色のよいリゾート地帯を通過します。
後から調べてわかったのですが、このルートはかつての中山道に並行しており、長和町を経由する国道142号線がほぼ中山道を辿ったルートになっています。中山道を忠実に辿る路線バスの旅というのもちょっと惹かれましたが、江戸時代も難所だった和田峠(長和町〜下諏訪町間)が現在も難所で、ここを通過する路線がなく歩くのもちょっとしんどい。今回はバスだけで乗り継げる白樺湖経由のルートにしました。
大阪を早朝に出発すると、佐久平駅へは昼前に着きます。北陸新幹線は便利です。


佐久平駅から千曲バスで立科町役場前まで行きます。このバスは立科町役場前行なのに、バス乗り場には時刻表を含めて「望月・芦田方面行」としか書かれてないので戸惑いました。地域名で行先を書くのは部外者にはわかりにくいです。

路線名が「中仙道線」とあるとおり、ほぼ中山道に沿ったルートを走ります。始発の岩村田、途中の塩名田、八幡、望月、終点の芦田はどれも旧宿場町です。



立科町役場前での乗り継ぎの時間を使って、芦田宿跡を散策しました。本陣跡やちょっとした案内所がありましたが、観光地として賑わう様子はありません。


ここから立科町営の「たてしなスマイル交通」で東白樺湖に向かいます。地図を見ると芦田から白樺湖の東半分まで狭い回廊のように立科町域が伸びており、その間をこのバスが結んでいるのです。

雨が降ってきましたが、緑深い高原地帯に入り、途中蓼科牧場や女神湖を横に見ながら景色のよい道を走ります。白樺湖に近づくにつれて観光客がパラパラと乗ってきました。



終点の東白樺湖のあたりはすっかりレジャーランドの様相で、盆休みの真っ只中なので車や人でごった返していました。


ここからアルピコ交通のバスで上諏訪駅まで行きます。この路線は茅野駅から白樺湖、車山高原、霧ヶ峰を回って上諏訪駅までを結ぶ、なかなかのロングラン路線です。

曇り空で、途中から激しく雨が降ってきましたが、霧ヶ峰高原はやはりなかなかの絶景でした。贅沢な路線バスです。





諏訪盆地へ下って行きます。諏訪湖をチラッと見て、上諏訪駅に到着です。



佐久から諏訪という鉄道が直接結んでいない2地点を路線バスで走破し、しかも雄大な景色も堪能できるという、ちょっと贅沢な路線バス旅でした。
【自由研究】超実数と距離空間(概要) [数学]
8/4に大阪で数学趣味の有志による「関西日曜数学友の会」が開催され、そこで私がタイトルの内容で発表しました。
発表のスライドを解説とともにここで公開します。

前半で超実数と超準解析についてのサワリを紹介し、後半で私の自由研究となる距離空間への応用を説明します。

まずは超実数とは何か、という説明です。実数体ℝは正確には 〈ℝ,+,∙,<,0,1〉で、その超準モデルは〈*ℝ,*+,*∙,*<,*0,*1〉(普通は演算等の*は省略して〈*ℝ,+,∙,<,0,1〉とかく)ですから、②の性質によって*ℝは順序体であり、実閉体でもあります。ただしデデキント完備性やアルキメデス性は一階の性質ではないので*ℝでは成立しません。
レーヴェンハイム・スコーレムの定理は「無限の領域を持つモデルはいくらでも大きな濃度の領域を持つモデルに拡大可能」ということを主張しますから、これらの性質をもつ超実数体*ℝはZFC上で存在し、また超積という手法を用いて実際に構成できます。これは無限の領域を持つどんなモデルであっても同じです。

超実数体における基本的な概念です。ここでℝ+は正実数の全体を表します。
これらの存在証明は、まず④から始まります。aが有限超実数(無限大でない超実数)であれば、それとの大小関係によるℝのデデキント切断が存在し、その境界となる実数cが定まるので、c=st(a) となります。次に①と②は互いに逆数関係になるのでどちらか一方の存在を証明すればよく、aを実数ではない超実数とすると、これが無限大超実数であればそれでよし、そうでなければ a-st(a) が0でない無限小超実数となります。
無限小超実数の全体は加法群であり、従って③の ≈ は同値関係です。また無限小超実数と有限超実数との積は無限小超実数ですから、無限小超実数の全体は有限超実数全体のなす環におけるイデアルとなり、それによる剰余環はℝと同型になります。
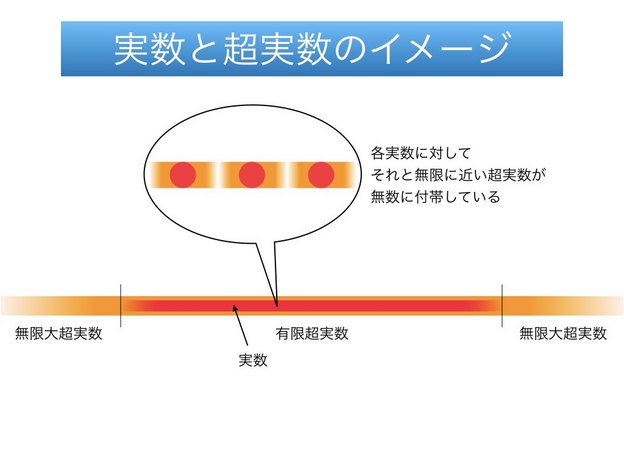
あまり正しい表現とは言えませんが、実数と超実数の関係を表すイメージ図です(実際には実数はこのような飛び飛びではありませんね)。実数のまわりに有限超実数がまとわりつき、その正負両方向の外側に無限大超実数が広がります。

超準解析のほんのサワリです。ℝの関数fを*ℝの関数*fに自然拡張するのは、これもモデル理論によって存在が示されますが、超積を用いても構成できます。これは何変数関数でも同様で、また関数だけではなく関係についても同様に自然拡張が存在します。部分集合は1変数の関係とみなせますのでこれも自然拡張できます。例えば自然数の全体ℕを超自然数の全体*ℕに拡張できます。
微分の表現を見るとわかるように、「無限小変化の比の標準部分」が微分係数です。dx,dyは何を表すのか理解しにくかったのですが、Δx,Δyの方は無限小超実数という「数」であり、四則演算が自由に行えるところが超準解析の醍醐味となります。例えばここから関数の積の導関数の公式が数式の四則演算処理でいとも簡単に導かれます。もう一つ例をあげると、ロピタルの定理の∞/∞バージョンの証明は通常のやり方では少々面倒臭いのですが、超実数を使うと無限大の範囲でコーシーの平均値の定理が成り立ちますので、もうちょっとスッキリした証明ができます。
ここまではネットでも調べることができる超実数と超準解析の紹介でした。ここからが私の自由研究になります。

一般の距離空間(ただし領域は無限集合とします)についても、超準モデルが考えられます。このとき距離関数dの自然拡張*dは移行原理によって*Xから*ℝへの2変数関数になります。距離関数の性質i)〜iii)は全て一階の性質ですから、*dも同じ性質をもちます。この*dによる「*距離」が無限小であることをもって「2点が無限に近い」という関係 ≈ が定義でき、明らかにこれは同値関係です。

距離空間における色々な概念が、超準モデルを用いた簡単な論理式と同値になるということを説明しています。これらの証明はℝにおける超準解析と類似の手法で行えます。①の開集合の場合を日本語でかくと「Aの点と無限に近い*Xの点は全て*Aの点である」となります。オレンジで書かれた定理は①と③の論理式を突き合わせるだけで簡単に導けますね。

同様に、コンパクト性とそれに関連する諸概念を超準モデルを用いた同値な論理式で表したものです(特にコンパクト性はいかにも強力な性質にみえます)。これらの証明は少々複雑ですが、難しいものではありません。オレンジ色で書かれた距離空間における有名な定理は、やはりこれらの論理式を突き合わせると簡単に導けます。具体的には、赤色から青色が従うことは明らかですから①→②、あとは赤色と青色の対応をみることで①→③と②∧③→①が簡単にわかります。

最後に、超準モデルを用いた距離空間の完備化です。コーシー列を用いた完備化と本質的に変わらないかもしれませんが、距離空間の「点」や「距離」と同じように扱えるため、よりわかりやすくなっているように思います。
発表内容は以上でした。距離空間への応用は面白いので、もう少し深く掘り下げていこうと思います。
発表のスライドを解説とともにここで公開します。

前半で超実数と超準解析についてのサワリを紹介し、後半で私の自由研究となる距離空間への応用を説明します。

まずは超実数とは何か、という説明です。実数体ℝは正確には 〈ℝ,+,∙,<,0,1〉で、その超準モデルは〈*ℝ,*+,*∙,*<,*0,*1〉(普通は演算等の*は省略して〈*ℝ,+,∙,<,0,1〉とかく)ですから、②の性質によって*ℝは順序体であり、実閉体でもあります。ただしデデキント完備性やアルキメデス性は一階の性質ではないので*ℝでは成立しません。
レーヴェンハイム・スコーレムの定理は「無限の領域を持つモデルはいくらでも大きな濃度の領域を持つモデルに拡大可能」ということを主張しますから、これらの性質をもつ超実数体*ℝはZFC上で存在し、また超積という手法を用いて実際に構成できます。これは無限の領域を持つどんなモデルであっても同じです。

超実数体における基本的な概念です。ここでℝ+は正実数の全体を表します。
これらの存在証明は、まず④から始まります。aが有限超実数(無限大でない超実数)であれば、それとの大小関係によるℝのデデキント切断が存在し、その境界となる実数cが定まるので、c=st(a) となります。次に①と②は互いに逆数関係になるのでどちらか一方の存在を証明すればよく、aを実数ではない超実数とすると、これが無限大超実数であればそれでよし、そうでなければ a-st(a) が0でない無限小超実数となります。
無限小超実数の全体は加法群であり、従って③の ≈ は同値関係です。また無限小超実数と有限超実数との積は無限小超実数ですから、無限小超実数の全体は有限超実数全体のなす環におけるイデアルとなり、それによる剰余環はℝと同型になります。

あまり正しい表現とは言えませんが、実数と超実数の関係を表すイメージ図です(実際には実数はこのような飛び飛びではありませんね)。実数のまわりに有限超実数がまとわりつき、その正負両方向の外側に無限大超実数が広がります。

超準解析のほんのサワリです。ℝの関数fを*ℝの関数*fに自然拡張するのは、これもモデル理論によって存在が示されますが、超積を用いても構成できます。これは何変数関数でも同様で、また関数だけではなく関係についても同様に自然拡張が存在します。部分集合は1変数の関係とみなせますのでこれも自然拡張できます。例えば自然数の全体ℕを超自然数の全体*ℕに拡張できます。
微分の表現を見るとわかるように、「無限小変化の比の標準部分」が微分係数です。dx,dyは何を表すのか理解しにくかったのですが、Δx,Δyの方は無限小超実数という「数」であり、四則演算が自由に行えるところが超準解析の醍醐味となります。例えばここから関数の積の導関数の公式が数式の四則演算処理でいとも簡単に導かれます。もう一つ例をあげると、ロピタルの定理の∞/∞バージョンの証明は通常のやり方では少々面倒臭いのですが、超実数を使うと無限大の範囲でコーシーの平均値の定理が成り立ちますので、もうちょっとスッキリした証明ができます。
ここまではネットでも調べることができる超実数と超準解析の紹介でした。ここからが私の自由研究になります。

一般の距離空間(ただし領域は無限集合とします)についても、超準モデルが考えられます。このとき距離関数dの自然拡張*dは移行原理によって*Xから*ℝへの2変数関数になります。距離関数の性質i)〜iii)は全て一階の性質ですから、*dも同じ性質をもちます。この*dによる「*距離」が無限小であることをもって「2点が無限に近い」という関係 ≈ が定義でき、明らかにこれは同値関係です。

距離空間における色々な概念が、超準モデルを用いた簡単な論理式と同値になるということを説明しています。これらの証明はℝにおける超準解析と類似の手法で行えます。①の開集合の場合を日本語でかくと「Aの点と無限に近い*Xの点は全て*Aの点である」となります。オレンジで書かれた定理は①と③の論理式を突き合わせるだけで簡単に導けますね。

同様に、コンパクト性とそれに関連する諸概念を超準モデルを用いた同値な論理式で表したものです(特にコンパクト性はいかにも強力な性質にみえます)。これらの証明は少々複雑ですが、難しいものではありません。オレンジ色で書かれた距離空間における有名な定理は、やはりこれらの論理式を突き合わせると簡単に導けます。具体的には、赤色から青色が従うことは明らかですから①→②、あとは赤色と青色の対応をみることで①→③と②∧③→①が簡単にわかります。

最後に、超準モデルを用いた距離空間の完備化です。コーシー列を用いた完備化と本質的に変わらないかもしれませんが、距離空間の「点」や「距離」と同じように扱えるため、よりわかりやすくなっているように思います。
発表内容は以上でした。距離空間への応用は面白いので、もう少し深く掘り下げていこうと思います。



