わかってない奴がわかったつもりで書き留める超準解析(その4) [数学]
【超準解析について生半可な知識しかない僕が、わかったつもりの内容をちょっとずつ書き留めていきます。不正確な内容や誤りもあることをご承知ください。】
(4) 微分
極限が超準解析でシンプルに表現できたので、微分も同様にシンプルに表現できます。
$f : \mathbb{R} \to \mathbb{R}$とします。$f$に対して2変数関数 $df : \mathbb{R}^2 \to \mathbb{R}$ を次で定めます。
\[ df(x,dx) = f(x+dx)-f(x) \]
ここで $x,dx$ はどちらも$\mathbb{R}$上を動く変数です。ここで$x$に対して極限値
\[ \lim_{dx \to 0} \frac{df(x,dx)}{dx} \]
が存在するならば、$f$は$x$で微分可能でその極限値を $f'(x)$ とかくのでした。
これを超準解析で表現すると次のようになります。$f$の超準拡大 ${}^*f : {}^*\mathbb{R} \to {}^*\mathbb{R}$ がとれることと同様に、$df$も超準拡大 ${}^*df : {}^*\mathbb{R}^2 \to {}^*\mathbb{R}$ がとれて、
\[ {}^*df(x,dx) = {}^*f(x+dx)-{}^*f(x) \]
となります。$x,dx$ は${}^*\mathbb{R}$上を動く変数です。従って実数$x$に対して$f$が$x$で微分可能ならば、$dx \in \mathrm{monad}(0) \setminus \{ 0 \}$(0でない無限小)のとき、
\[ f'(x) = \mathrm{st} \left( \frac{{}^*df(x,dx)}{dx} \right) \]
あるいは
\[ f'(x) \approx \frac{{}^*df(x,dx)}{dx} \]
が成り立つことになります。
$dx$が無限小のときは、${}^*df(x,dx)$ は$f$の$x$における無限小の差分といえますので、微分とは「無限小の差分の比」という意味になることが上の表現からわかります。ここで${}^*\mathbb{R}$上を動く変数 $y,dy$ が
\[y={}^*f(x), \quad dy={}^*df(x,dx) \]
をみたすものとすると、$dx$が0でない無限小のとき
\[ f'(x) \approx \frac{dy}{dx} \]
となります。この右辺は微分の表現としてよく使われますが、その意味がこれでよく理解できますね。
別の関数$g$が$x$で微分可能とすると、同様に考えて$dx$が0でない無限小のとき、
\[ g'(x) \approx \frac{{}^*dg(x,dx)}{dx} \]
が成り立ちます。一方、
\[ \begin{align}
{}^*f(x+dx){}^*g(x+dx)-{}^*f(x){}^*g(x) &= {}^*f(x+dx)({}^*g(x+dx)-{}^*g(x))+({}^*f(x+dx)-{}^*f(x)){}^*g(x) \\
&= {}^*f(x+dx){}^*dg(x,dx)+{}^*df(x,dx){}^*g(x)
\end{align} \]
より、
\[ \frac{{}^*f(x+dx){}^*g(x+dx)-{}^*f(x){}^*g(x)}{dx} = {}^*f(x+dx) \frac{{}^*dg(x,dx)}{dx}+ \frac{{}^*df(x,dx)}{dx}{}^*g(x) \]
となるので、$f$が$x$で連続であることを考慮すると、$dx$が0でない無限小のとき次式となります。
\[ \frac{{}^*f(x+dx){}^*g(x+dx)-{}^*f(x){}^*g(x)}{dx} \approx f(x)g'(x)+f'(x)g(x) \]
従って$f$と$g$の積 $fg$ も$x$で微分可能となり、よく知られた積の微分公式が得られます。
2階の導関数についても表現してみましょう。2変数関数 $d^2f : \mathbb{R}^2 \to \mathbb{R}$ を$df$を用いて次で定めます。
\[ d^2f(x,dx) = df(x+dx,dx)-df(x,dx) \]
これに対して超準拡大 ${}^*d^2f : {}^*\mathbb{R}^2 \to {}^*\mathbb{R}$ がとれることも同様です。
実数$x$のある近傍で$f$が2回連続微分可能とします。このとき平均値の定理と移行原理より、$dx$が十分小さければ、
\[ {}^*df(x+dx,dx) = {}^*f'(x+dx+ \alpha dx)dx \\
{}^*df(x,dx) = {}^*f'(x+ \beta dx)dx \]
をみたす $\alpha, \beta \ (0 < \alpha < 1, 0 < \beta < 1)$ が存在します。$f'$ に対して再度平均値の定理と移行原理を用いると、
\[ {}^*f'(x+dx+ \alpha dx) - {}^*f'(x+ \beta dx) = {}^*f''(x + \gamma dx)dx \]
をみたす $\gamma \ (0 < \gamma < 2)$ が存在します。合わせると、
\[ \begin{align}
{}^*d^2f(x,dx) &= {}^*df(x+dx,dx)-{}^*df(x,dx) \\
&= ({}^*f'(x+dx+ \alpha dx) - {}^*f'(x+ \beta dx))dx \\
&= {}^*f''(x + \gamma dx)dx^2
\end{align} \]
となりますが、$dx$が0でない無限小のときは $f''$ の連続性より、
\[ {}^*f''(x + \gamma dx) \approx f''(x) \]
がいえますので、
\[ f''(x) \approx \frac{{}^*d^2f(x,dx)}{dx^2} \]
が得られます。
変数 $d^2y$ が $d^2y = {}^*d^2f(x,dx)$ をみたすものとすると、
\[ f''(x) \approx \frac{d^2y}{dx^2} \]
とこれもおなじみの表現が得られます。
さらに高階の導関数についても同様です。
このように、超実数の世界で無限小や無限大を実数と同様な数として扱い、極限をその標準部分をとる操作として考えることによって、色々な証明がかなりシンプルになることがあります。例えばロピタルの定理の ∞/∞ バージョンについても、以前にこちらの記事で紹介したようなシンプルな証明が可能です。
(続く)(前記事)(目次)
(4) 微分
極限が超準解析でシンプルに表現できたので、微分も同様にシンプルに表現できます。
$f : \mathbb{R} \to \mathbb{R}$とします。$f$に対して2変数関数 $df : \mathbb{R}^2 \to \mathbb{R}$ を次で定めます。
\[ df(x,dx) = f(x+dx)-f(x) \]
ここで $x,dx$ はどちらも$\mathbb{R}$上を動く変数です。ここで$x$に対して極限値
\[ \lim_{dx \to 0} \frac{df(x,dx)}{dx} \]
が存在するならば、$f$は$x$で微分可能でその極限値を $f'(x)$ とかくのでした。
これを超準解析で表現すると次のようになります。$f$の超準拡大 ${}^*f : {}^*\mathbb{R} \to {}^*\mathbb{R}$ がとれることと同様に、$df$も超準拡大 ${}^*df : {}^*\mathbb{R}^2 \to {}^*\mathbb{R}$ がとれて、
\[ {}^*df(x,dx) = {}^*f(x+dx)-{}^*f(x) \]
となります。$x,dx$ は${}^*\mathbb{R}$上を動く変数です。従って実数$x$に対して$f$が$x$で微分可能ならば、$dx \in \mathrm{monad}(0) \setminus \{ 0 \}$(0でない無限小)のとき、
\[ f'(x) = \mathrm{st} \left( \frac{{}^*df(x,dx)}{dx} \right) \]
あるいは
\[ f'(x) \approx \frac{{}^*df(x,dx)}{dx} \]
が成り立つことになります。
$dx$が無限小のときは、${}^*df(x,dx)$ は$f$の$x$における無限小の差分といえますので、微分とは「無限小の差分の比」という意味になることが上の表現からわかります。ここで${}^*\mathbb{R}$上を動く変数 $y,dy$ が
\[y={}^*f(x), \quad dy={}^*df(x,dx) \]
をみたすものとすると、$dx$が0でない無限小のとき
\[ f'(x) \approx \frac{dy}{dx} \]
となります。この右辺は微分の表現としてよく使われますが、その意味がこれでよく理解できますね。
別の関数$g$が$x$で微分可能とすると、同様に考えて$dx$が0でない無限小のとき、
\[ g'(x) \approx \frac{{}^*dg(x,dx)}{dx} \]
が成り立ちます。一方、
\[ \begin{align}
{}^*f(x+dx){}^*g(x+dx)-{}^*f(x){}^*g(x) &= {}^*f(x+dx)({}^*g(x+dx)-{}^*g(x))+({}^*f(x+dx)-{}^*f(x)){}^*g(x) \\
&= {}^*f(x+dx){}^*dg(x,dx)+{}^*df(x,dx){}^*g(x)
\end{align} \]
より、
\[ \frac{{}^*f(x+dx){}^*g(x+dx)-{}^*f(x){}^*g(x)}{dx} = {}^*f(x+dx) \frac{{}^*dg(x,dx)}{dx}+ \frac{{}^*df(x,dx)}{dx}{}^*g(x) \]
となるので、$f$が$x$で連続であることを考慮すると、$dx$が0でない無限小のとき次式となります。
\[ \frac{{}^*f(x+dx){}^*g(x+dx)-{}^*f(x){}^*g(x)}{dx} \approx f(x)g'(x)+f'(x)g(x) \]
従って$f$と$g$の積 $fg$ も$x$で微分可能となり、よく知られた積の微分公式が得られます。
2階の導関数についても表現してみましょう。2変数関数 $d^2f : \mathbb{R}^2 \to \mathbb{R}$ を$df$を用いて次で定めます。
\[ d^2f(x,dx) = df(x+dx,dx)-df(x,dx) \]
これに対して超準拡大 ${}^*d^2f : {}^*\mathbb{R}^2 \to {}^*\mathbb{R}$ がとれることも同様です。
実数$x$のある近傍で$f$が2回連続微分可能とします。このとき平均値の定理と移行原理より、$dx$が十分小さければ、
\[ {}^*df(x+dx,dx) = {}^*f'(x+dx+ \alpha dx)dx \\
{}^*df(x,dx) = {}^*f'(x+ \beta dx)dx \]
をみたす $\alpha, \beta \ (0 < \alpha < 1, 0 < \beta < 1)$ が存在します。$f'$ に対して再度平均値の定理と移行原理を用いると、
\[ {}^*f'(x+dx+ \alpha dx) - {}^*f'(x+ \beta dx) = {}^*f''(x + \gamma dx)dx \]
をみたす $\gamma \ (0 < \gamma < 2)$ が存在します。合わせると、
\[ \begin{align}
{}^*d^2f(x,dx) &= {}^*df(x+dx,dx)-{}^*df(x,dx) \\
&= ({}^*f'(x+dx+ \alpha dx) - {}^*f'(x+ \beta dx))dx \\
&= {}^*f''(x + \gamma dx)dx^2
\end{align} \]
となりますが、$dx$が0でない無限小のときは $f''$ の連続性より、
\[ {}^*f''(x + \gamma dx) \approx f''(x) \]
がいえますので、
\[ f''(x) \approx \frac{{}^*d^2f(x,dx)}{dx^2} \]
が得られます。
変数 $d^2y$ が $d^2y = {}^*d^2f(x,dx)$ をみたすものとすると、
\[ f''(x) \approx \frac{d^2y}{dx^2} \]
とこれもおなじみの表現が得られます。
さらに高階の導関数についても同様です。
このように、超実数の世界で無限小や無限大を実数と同様な数として扱い、極限をその標準部分をとる操作として考えることによって、色々な証明がかなりシンプルになることがあります。例えばロピタルの定理の ∞/∞ バージョンについても、以前にこちらの記事で紹介したようなシンプルな証明が可能です。
(続く)(前記事)(目次)
わかってない奴がわかったつもりで書き留める超準解析(その3) [数学]
【超準解析について生半可な知識しかない僕が、わかったつもりの内容をちょっとずつ書き留めていきます。不正確な内容や誤りもあることをご承知ください。】
(3) 極限、連続、一様連続
高校数学では、関数の極限についてこう習ったと思います。
「$a$と異なる$x$が$a$に限りなく近づくならば関数$f$の値$f(x)$が$b$に限りなく近づくことを、$\displaystyle \lim_{x \to a} f(x) =b$ と表す。」
この「限りなく近づく」が数学の定義としてあまりに直感的すぎるいうことで、大学ではいわゆる「$\epsilon - \delta$ 論法」による厳密な極限の定義を習ったわけです。
しかし、超準解析における極限の定義は、この高校数学の直感的な定義をほぼそのまま使うことができます。
ここで${}^*f$は$f$の超準拡大であり、「無限に近い」とは前節で登場した超実数体${}^*\mathbb{R}$における関係$\approx$を意味するので、この定義は数学的に厳密な定義になっています。
では、この定義が $\epsilon - \delta$ 論法による定義と同値であることを証明しましょう。これは以下のように行われます。今後本シリーズを通して正実数の全体を$\mathbb{R}^+$、正超実数の全体を${}^*\mathbb{R}^+$で表すこととしますが、移行原理によって ${}^*(\mathbb{R}^+) = {}^*\mathbb{R}^+$ となることに注意してください。
まず、$\epsilon - \delta$ 論法による定義で $\displaystyle \lim_{x \to a} f(x) =b$ とする。任意に正実数$\epsilon$をとると、ある正実数$\delta$が存在して、
\[ \forall x \in \mathbb{R} \, ( 0< \left| x-a \right| < \delta \to \left| f(x)-b \right| < \epsilon ) \]
が成り立つようにできる。$\epsilon, \delta$を定数とみて移行原理を適用すると、
\[ \forall x \in {}^*\mathbb{R} \, ( 0< \left| x-a \right| < \delta \to \left| {}^*f(x)-b \right| < \epsilon ) \]
が成り立つ。$\delta$は正実数だから、
\[ \forall x \in {}^*\mathbb{R} \, ( x \approx a \land x \neq a \to \left| {}^*f(x)-b \right| < \epsilon ) \]
が成り立ち、$\epsilon$は任意の正実数だから、
\[ \forall x \in {}^*\mathbb{R} \, ( x \approx a \land x \neq a \to {}^*f(x) \approx b ) \]
が成り立つ。従って超準解析における定義でも $\displaystyle \lim_{x \to a} f(x) =b$ である。
次に、超準解析における定義で $\displaystyle \lim_{x \to a} f(x) =b$ とする。任意に正実数$\epsilon$をとると、
\[ \exists \delta \in {}^*\mathbb{R}^+ \, \forall x \in {}^*\mathbb{R} \, ( 0< \left| x-a \right| < \delta \to \left| {}^*f(x)-b \right| < \epsilon ) \]
が成り立つ。なぜなら$\delta$が正の無限小超実数であればこれをみたすからである。移行原理より、
\[ \exists \delta \in \mathbb{R}^+ \, \forall x \in \mathbb{R} \, ( 0< \left| x-a \right| < \delta \to \left| f(x)-b \right| < \epsilon ) \]
が成り立つが、$\epsilon$が任意の正実数にとれるから、
\[ \forall \epsilon \in \mathbb{R}^+ \, \exists \delta \in \mathbb{R}^+ \, \forall x \in \mathbb{R} \, ( 0< \left| x-a \right| < \delta \to \left| f(x)-b \right| < \epsilon ) \]
が成り立つ。従って $\epsilon - \delta$ 論法による定義でも $\displaystyle \lim_{x \to a} f(x) =b$ である。□
$\epsilon$や$\delta$を定数とみたり変数とみたり都合よく使い分けながら移行原理を用いることで、うまく証明できました。
ここで、超実数$x$に対して$x$の単子(モナド)と呼ばれる
\[ \mathrm{monad}(x) = \{ \, y \in {}^*\mathbb{R} \, \mid \, y \approx x \, \} \]
によって定義される集合を用いると、
\[ \lim_{x \to a} f(x) =b \quad \Leftrightarrow \quad \forall x \in \mathrm{monad}(a) \setminus \{ a \} \, ({}^*f(x) \in \mathrm{monad}(b)) \]
と表すことができます。そしてこのとき、
\[ \lim_{x \to a} f(x) = \mathrm{st}({}^*f(x)) \ \mathrm{for \ all} \ x \in \mathrm{monad}(a) \setminus \{ a \} \]
が成り立ちます。
$x \to +\infty$ のときの極限についても同様に、
\[ \lim_{x \to +\infty} f(x) =b \quad \Leftrightarrow \quad \forall x \in {}^*\mathbb{R}^+_\infty \, ({}^*f(x) \in \mathrm{monad}(b)) \]
によって表せます。ここで ${}^*\mathbb{R}^+_\infty$ は正の無限大超実数の全体を表し、従ってこれは超実数$x$が無限に大きいならば ${}^*f(x)$ が実数$b$に無限に近いことを意味します。そしてこのとき、
\[ \lim_{x \to +\infty} f(x) = \mathrm{st}({}^*f(x)) \ \mathrm{for \ all} \ x \in {}^*\mathbb{R}^+_\infty \]
が成り立ちます。
極限に関する以上の結果から、関数の連続性については、
\begin{eqnarray*}
f \, \text{が} \, a \, \text{で連続} \quad &\Leftrightarrow& \quad \forall x \in {}^*\mathbb{R} \, (x \approx a \to {}^*f(x) \approx f(a)) \\
\quad &\Leftrightarrow& \quad \forall x \in \mathrm{monad}(a) \, ({}^*f(x) \in \mathrm{monad}(f(a)))
\end{eqnarray*}
と表せます。そしてこのとき、
\[ f(a) = \mathrm{st}({}^*f(x)) \ \mathrm{for \ all} \ x \in \mathrm{monad}(a) \]
が成り立ちます。
さらに、$A$を$\mathbb{R}$の部分集合とするとき、関数の一様連続性について、
\[ f \, \text{が} \, A \, \text{で一様連続} \quad \Leftrightarrow \quad \forall x,y \in {}^*A \, (x \approx y \to {}^*f(x) \approx {}^*f(y)) \]
と表せます。これが通常の $\epsilon - \delta$ 論法による一様連続の定義と同値であることは、極限と同様のやり方で証明できます。
極限、連続性、一様連続性のいずれも、超準解析を用いると非常にシンプルな表現になりますね。
定理の証明もシンプルになることを次の例で示しておきます。
(証明)$A=[a,b]$ とおくと、移行原理より ${}^*A=[a,b]$(${}^*\mathbb{R}$の区間)である。任意に $x,y \in {}^*A \land x \approx y$ となる$x,y$をとると、$z=\mathrm{st}(x)=\mathrm{st}(y)$ となる $z \in A$ がとれて、$f$が$z$で連続だから ${}^*f(x) \approx f(z) \approx {}^*f(y)$ より ${}^*f(x) \approx {}^*f(y)$ である。従って$f$は$A$で一様連続である。□
(続く)(前記事)(目次)
(3) 極限、連続、一様連続
高校数学では、関数の極限についてこう習ったと思います。
「$a$と異なる$x$が$a$に限りなく近づくならば関数$f$の値$f(x)$が$b$に限りなく近づくことを、$\displaystyle \lim_{x \to a} f(x) =b$ と表す。」
この「限りなく近づく」が数学の定義としてあまりに直感的すぎるいうことで、大学ではいわゆる「$\epsilon - \delta$ 論法」による厳密な極限の定義を習ったわけです。
しかし、超準解析における極限の定義は、この高校数学の直感的な定義をほぼそのまま使うことができます。
【極限の定義】
$f : \mathbb{R} \to \mathbb{R}$ とする。実数$a$と異なる超実数$x$が$a$に無限に近いならば ${}^*f(x)$ が実数$b$に無限に近いことを、$\displaystyle \lim_{x \to a} f(x) =b$ と表す。式でかくと次のとおり。
\[ \lim_{x \to a} f(x) =b \quad \Leftrightarrow \quad \forall x \in {}^*\mathbb{R} \, (x \approx a \land x \neq a \to {}^*f(x) \approx b) \]
ここで${}^*f$は$f$の超準拡大であり、「無限に近い」とは前節で登場した超実数体${}^*\mathbb{R}$における関係$\approx$を意味するので、この定義は数学的に厳密な定義になっています。
では、この定義が $\epsilon - \delta$ 論法による定義と同値であることを証明しましょう。これは以下のように行われます。今後本シリーズを通して正実数の全体を$\mathbb{R}^+$、正超実数の全体を${}^*\mathbb{R}^+$で表すこととしますが、移行原理によって ${}^*(\mathbb{R}^+) = {}^*\mathbb{R}^+$ となることに注意してください。
まず、$\epsilon - \delta$ 論法による定義で $\displaystyle \lim_{x \to a} f(x) =b$ とする。任意に正実数$\epsilon$をとると、ある正実数$\delta$が存在して、
\[ \forall x \in \mathbb{R} \, ( 0< \left| x-a \right| < \delta \to \left| f(x)-b \right| < \epsilon ) \]
が成り立つようにできる。$\epsilon, \delta$を定数とみて移行原理を適用すると、
\[ \forall x \in {}^*\mathbb{R} \, ( 0< \left| x-a \right| < \delta \to \left| {}^*f(x)-b \right| < \epsilon ) \]
が成り立つ。$\delta$は正実数だから、
\[ \forall x \in {}^*\mathbb{R} \, ( x \approx a \land x \neq a \to \left| {}^*f(x)-b \right| < \epsilon ) \]
が成り立ち、$\epsilon$は任意の正実数だから、
\[ \forall x \in {}^*\mathbb{R} \, ( x \approx a \land x \neq a \to {}^*f(x) \approx b ) \]
が成り立つ。従って超準解析における定義でも $\displaystyle \lim_{x \to a} f(x) =b$ である。
次に、超準解析における定義で $\displaystyle \lim_{x \to a} f(x) =b$ とする。任意に正実数$\epsilon$をとると、
\[ \exists \delta \in {}^*\mathbb{R}^+ \, \forall x \in {}^*\mathbb{R} \, ( 0< \left| x-a \right| < \delta \to \left| {}^*f(x)-b \right| < \epsilon ) \]
が成り立つ。なぜなら$\delta$が正の無限小超実数であればこれをみたすからである。移行原理より、
\[ \exists \delta \in \mathbb{R}^+ \, \forall x \in \mathbb{R} \, ( 0< \left| x-a \right| < \delta \to \left| f(x)-b \right| < \epsilon ) \]
が成り立つが、$\epsilon$が任意の正実数にとれるから、
\[ \forall \epsilon \in \mathbb{R}^+ \, \exists \delta \in \mathbb{R}^+ \, \forall x \in \mathbb{R} \, ( 0< \left| x-a \right| < \delta \to \left| f(x)-b \right| < \epsilon ) \]
が成り立つ。従って $\epsilon - \delta$ 論法による定義でも $\displaystyle \lim_{x \to a} f(x) =b$ である。□
$\epsilon$や$\delta$を定数とみたり変数とみたり都合よく使い分けながら移行原理を用いることで、うまく証明できました。
ここで、超実数$x$に対して$x$の単子(モナド)と呼ばれる
\[ \mathrm{monad}(x) = \{ \, y \in {}^*\mathbb{R} \, \mid \, y \approx x \, \} \]
によって定義される集合を用いると、
\[ \lim_{x \to a} f(x) =b \quad \Leftrightarrow \quad \forall x \in \mathrm{monad}(a) \setminus \{ a \} \, ({}^*f(x) \in \mathrm{monad}(b)) \]
と表すことができます。そしてこのとき、
\[ \lim_{x \to a} f(x) = \mathrm{st}({}^*f(x)) \ \mathrm{for \ all} \ x \in \mathrm{monad}(a) \setminus \{ a \} \]
が成り立ちます。
$x \to +\infty$ のときの極限についても同様に、
\[ \lim_{x \to +\infty} f(x) =b \quad \Leftrightarrow \quad \forall x \in {}^*\mathbb{R}^+_\infty \, ({}^*f(x) \in \mathrm{monad}(b)) \]
によって表せます。ここで ${}^*\mathbb{R}^+_\infty$ は正の無限大超実数の全体を表し、従ってこれは超実数$x$が無限に大きいならば ${}^*f(x)$ が実数$b$に無限に近いことを意味します。そしてこのとき、
\[ \lim_{x \to +\infty} f(x) = \mathrm{st}({}^*f(x)) \ \mathrm{for \ all} \ x \in {}^*\mathbb{R}^+_\infty \]
が成り立ちます。
極限に関する以上の結果から、関数の連続性については、
\begin{eqnarray*}
f \, \text{が} \, a \, \text{で連続} \quad &\Leftrightarrow& \quad \forall x \in {}^*\mathbb{R} \, (x \approx a \to {}^*f(x) \approx f(a)) \\
\quad &\Leftrightarrow& \quad \forall x \in \mathrm{monad}(a) \, ({}^*f(x) \in \mathrm{monad}(f(a)))
\end{eqnarray*}
と表せます。そしてこのとき、
\[ f(a) = \mathrm{st}({}^*f(x)) \ \mathrm{for \ all} \ x \in \mathrm{monad}(a) \]
が成り立ちます。
さらに、$A$を$\mathbb{R}$の部分集合とするとき、関数の一様連続性について、
\[ f \, \text{が} \, A \, \text{で一様連続} \quad \Leftrightarrow \quad \forall x,y \in {}^*A \, (x \approx y \to {}^*f(x) \approx {}^*f(y)) \]
と表せます。これが通常の $\epsilon - \delta$ 論法による一様連続の定義と同値であることは、極限と同様のやり方で証明できます。
極限、連続性、一様連続性のいずれも、超準解析を用いると非常にシンプルな表現になりますね。
定理の証明もシンプルになることを次の例で示しておきます。
【定理】$f$を$\mathbb{R}$の有界閉区間 $[a,b]$ から$\mathbb{R}$への連続関数とすると、$f$はこの区間上で一様連続である。
(証明)$A=[a,b]$ とおくと、移行原理より ${}^*A=[a,b]$(${}^*\mathbb{R}$の区間)である。任意に $x,y \in {}^*A \land x \approx y$ となる$x,y$をとると、$z=\mathrm{st}(x)=\mathrm{st}(y)$ となる $z \in A$ がとれて、$f$が$z$で連続だから ${}^*f(x) \approx f(z) \approx {}^*f(y)$ より ${}^*f(x) \approx {}^*f(y)$ である。従って$f$は$A$で一様連続である。□
(続く)(前記事)(目次)
わかってない奴がわかったつもりで書き留める超準解析(その2) [数学]
【超準解析について生半可な知識しかない僕が、わかったつもりの内容をちょっとずつ書き留めていきます。不正確な内容や誤りもあることをご承知ください。】
(2) 実数体の超準モデル「超実数体」
実数の全体$\mathbb{R}$上には、順序関係$\le$、加法演算$+$、乗法演算 $\cdot$ と定数$0,1$が与えられ、それらに対してよく知られた一連の公理系が成立し、$\langle \mathbb{R}, \le, +, \cdot, 0,1 \rangle$ は実数体と呼ばれます(以下、実数体のことを簡単に$\mathbb{R}$で表します)。
ここで、2項演算は2変数関数であり、また定数は0変数関数であるので、第1回での一般的な議論が$\mathbb{R}$に対してもいえます。つまり、実数体を真に拡大する超準モデル $\langle {}^*\mathbb{R}, {}^*\le, {}^*+, {}^*\cdot, {}^*0,{}^*1 \rangle$ が存在します。これを超実数体と呼びます(これも以下簡単に${}^*\mathbb{R}$で表します)。さらに${}^*\mathbb{R}$の元を超実数と呼びます。
${}^*\le, {}^*+, {}^*\cdot$ はそれぞれ $\le, +, \cdot$ の拡大ですが、${}^*$は通常省略されます。また定数 ${}^*0,{}^*1$ はそれぞれ $0,1$ と一致しますのでこれらも${}^*$は必要ありません。
実数体の公理のうち、順序体の公理はすべて一階の論理式なので${}^*\mathbb{R}$でも成り立ちます。従って${}^*\mathbb{R}$は順序体です(なので${}^*\mathbb{R}$を超実数体と呼ぶことに何の問題もありません)。これに対し「実数体の完備性」と呼ばれる性質は一階の論理式で表現することができませんので、${}^*\mathbb{R}$で成り立つとはいえません。実際にも${}^*\mathbb{R}$では完備性が成り立たないことがこの後で証明されます。
では、超実数体${}^*\mathbb{R}$とは一体どんなものでしょうか。
${}^*\mathbb{R}$が$\mathbb{R}$を真に拡大するので、実数でない超実数が少なくとも1つ存在します。これを$a$とかくと、順序体の性質から次の2つのどちらかが成り立ちます。
① $a$の絶対値 $|a|$ はどんな実数よりも大きい($a$は無限大超実数)。
② $b < a < c$ となる実数$b,c$が存在する($a$は有限超実数)。
実は、①をみたす$a$と②をみたす$a$のどちらも存在します。それをこれから証明します。
まず、$a$が①をみたすとします。このとき逆数 $a^{-1} $が超実数として存在します。これは任意の正実数$b$に対して $0 < |a^{-1}| < b$ をみたすので、②をみたす実数でない超実数$a$が存在することになります。
任意の正実数$b$に対して $|a| < b$ をみたす$a$を無限小超実数と呼びます。$a$が0以外の無限小超実数ならば $a^{-1}$ は無限大超実数になり、その逆も成り立つことは明らかです。
次に、$a$が②をみたすとします。このとき、
\[
A = \{ x \in \mathbb{R} \mid x < a \} \\
B = \{ x \in \mathbb{R} \mid x > a \}
\]
とおくと、$\langle A,B \rangle$ は$\mathbb{R}$の「デデキントの切断」になるので、実数体の完備性より境界となる実数$d$が存在します。そして $e=a-d$ とおくと$e$は0以外の無限小超実数であることが容易にわかります。従ってその逆数 $e^{-1}$ は無限大超実数、すなわち①をみたす$a$が存在することになります。
以上で①をみたす$a$と②をみたす$a$のどちらも存在することが証明されました。つまり超実数は無限大超実数と有限超実数に分けられ、さらに有限超実数の特別なものとして無限小超実数がある、そして無限大超実数と0でない無限小超実数のいずれも存在する、ということになります。これらが無数に存在することも${}^*\mathbb{R}$が順序体であることから明らかです。
2つの超実数$a,b$について $a-b$ が無限小超実数であることを、「$a$と$b$は無限に近い」といい、
\[ a \approx b \]
と書きます。これは${}^*\mathbb{R}$上の同値関係です。0でない無限小超実数が無数に存在しますので、任意の超実数にはそれと無限に近い超実数が無数に存在することになります。
また、$a$が有限超実数ならば $b \approx a$ をみたす実数$b$が存在することが先ほど示されましたので、この$b$を $\mathrm{st}(a)$ とかき、$a$の標準部分と呼びます(唯一性は明らか)。つまり有限超実数は必ず標準部分をもつということになります。
以上のことから、超実数体${}^*\mathbb{R}$のイメージを図にすると、次のような感じになるでしょうか。
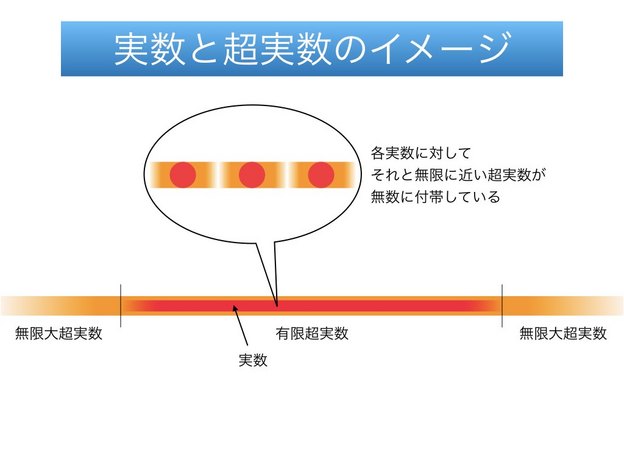
平たくいうと、超実数とは無限大や無限小を四則演算や大小比較のできる「数」として扱えるようにしたもの、といえます。
なお、$\mathbb{R}$で成り立つ完備性が${}^*\mathbb{R}$で成り立たないことは、有限超実数の全体が${}^*\mathbb{R}$において上限を持ち得ないことからわかります。そんなものがもしあれば、「最大の実数」の存在が示されるなど、すぐに矛盾が導かれてしまうからです。
(続く)(前記事)(目次)
(2) 実数体の超準モデル「超実数体」
実数の全体$\mathbb{R}$上には、順序関係$\le$、加法演算$+$、乗法演算 $\cdot$ と定数$0,1$が与えられ、それらに対してよく知られた一連の公理系が成立し、$\langle \mathbb{R}, \le, +, \cdot, 0,1 \rangle$ は実数体と呼ばれます(以下、実数体のことを簡単に$\mathbb{R}$で表します)。
ここで、2項演算は2変数関数であり、また定数は0変数関数であるので、第1回での一般的な議論が$\mathbb{R}$に対してもいえます。つまり、実数体を真に拡大する超準モデル $\langle {}^*\mathbb{R}, {}^*\le, {}^*+, {}^*\cdot, {}^*0,{}^*1 \rangle$ が存在します。これを超実数体と呼びます(これも以下簡単に${}^*\mathbb{R}$で表します)。さらに${}^*\mathbb{R}$の元を超実数と呼びます。
${}^*\le, {}^*+, {}^*\cdot$ はそれぞれ $\le, +, \cdot$ の拡大ですが、${}^*$は通常省略されます。また定数 ${}^*0,{}^*1$ はそれぞれ $0,1$ と一致しますのでこれらも${}^*$は必要ありません。
実数体の公理のうち、順序体の公理はすべて一階の論理式なので${}^*\mathbb{R}$でも成り立ちます。従って${}^*\mathbb{R}$は順序体です(なので${}^*\mathbb{R}$を超実数体と呼ぶことに何の問題もありません)。これに対し「実数体の完備性」と呼ばれる性質は一階の論理式で表現することができませんので、${}^*\mathbb{R}$で成り立つとはいえません。実際にも${}^*\mathbb{R}$では完備性が成り立たないことがこの後で証明されます。
では、超実数体${}^*\mathbb{R}$とは一体どんなものでしょうか。
${}^*\mathbb{R}$が$\mathbb{R}$を真に拡大するので、実数でない超実数が少なくとも1つ存在します。これを$a$とかくと、順序体の性質から次の2つのどちらかが成り立ちます。
① $a$の絶対値 $|a|$ はどんな実数よりも大きい($a$は無限大超実数)。
② $b < a < c$ となる実数$b,c$が存在する($a$は有限超実数)。
実は、①をみたす$a$と②をみたす$a$のどちらも存在します。それをこれから証明します。
まず、$a$が①をみたすとします。このとき逆数 $a^{-1} $が超実数として存在します。これは任意の正実数$b$に対して $0 < |a^{-1}| < b$ をみたすので、②をみたす実数でない超実数$a$が存在することになります。
任意の正実数$b$に対して $|a| < b$ をみたす$a$を無限小超実数と呼びます。$a$が0以外の無限小超実数ならば $a^{-1}$ は無限大超実数になり、その逆も成り立つことは明らかです。
次に、$a$が②をみたすとします。このとき、
\[
A = \{ x \in \mathbb{R} \mid x < a \} \\
B = \{ x \in \mathbb{R} \mid x > a \}
\]
とおくと、$\langle A,B \rangle$ は$\mathbb{R}$の「デデキントの切断」になるので、実数体の完備性より境界となる実数$d$が存在します。そして $e=a-d$ とおくと$e$は0以外の無限小超実数であることが容易にわかります。従ってその逆数 $e^{-1}$ は無限大超実数、すなわち①をみたす$a$が存在することになります。
以上で①をみたす$a$と②をみたす$a$のどちらも存在することが証明されました。つまり超実数は無限大超実数と有限超実数に分けられ、さらに有限超実数の特別なものとして無限小超実数がある、そして無限大超実数と0でない無限小超実数のいずれも存在する、ということになります。これらが無数に存在することも${}^*\mathbb{R}$が順序体であることから明らかです。
2つの超実数$a,b$について $a-b$ が無限小超実数であることを、「$a$と$b$は無限に近い」といい、
\[ a \approx b \]
と書きます。これは${}^*\mathbb{R}$上の同値関係です。0でない無限小超実数が無数に存在しますので、任意の超実数にはそれと無限に近い超実数が無数に存在することになります。
また、$a$が有限超実数ならば $b \approx a$ をみたす実数$b$が存在することが先ほど示されましたので、この$b$を $\mathrm{st}(a)$ とかき、$a$の標準部分と呼びます(唯一性は明らか)。つまり有限超実数は必ず標準部分をもつということになります。
以上のことから、超実数体${}^*\mathbb{R}$のイメージを図にすると、次のような感じになるでしょうか。

平たくいうと、超実数とは無限大や無限小を四則演算や大小比較のできる「数」として扱えるようにしたもの、といえます。
なお、$\mathbb{R}$で成り立つ完備性が${}^*\mathbb{R}$で成り立たないことは、有限超実数の全体が${}^*\mathbb{R}$において上限を持ち得ないことからわかります。そんなものがもしあれば、「最大の実数」の存在が示されるなど、すぐに矛盾が導かれてしまうからです。
(続く)(前記事)(目次)
わかってない奴がわかったつもりで書き留める超準解析(その1) [数学]
【超準解析について生半可な知識しかない僕が、わかったつもりの内容をちょっとずつ書き留めていきます。不正確な内容や誤りもあることをご承知ください。】
数学の知識をある程度つけた者が、超実数の世界では無限小やら無限大やらが自由に扱えることを知って、なんか面白いと思って超準解析をテキストでちゃんと勉強しようとします。するとそこには「ツェルメロ宇宙」やら「上部構造」やらのいきなり小難しい概念から始まるので、そこで萎えてしまうこともあろうかと思います。ここではもう少し簡単に、一般に数学モデルにはそれを拡大した「超準モデル」が存在することを説明し、それを実数体に適用することで「超実数体」が得られる、そして「移行原理」を駆使することで様々な性質が導ける、という順序で超準解析のサワリを紹介します。
(1) 超準モデルについて
一般に$X$を空でない集合とし、$R$を$X$上の2項関係すなわち $R \subseteq X^2$ とします。これらの対 $\langle X,R \rangle$ に対していくつかの公理系を与えると、それは一つの数学のモデルになります。$R$が3項以上の多項関係だったり、またそれらが複数個あったりしても以下の議論は同様に進められますが、簡単のためにここでは1つの2項関係だけのモデルを考えます。
例えば、述語記号$\le$を含む公理系$T$として
① $\forall x \, (x \le x)$
② $\forall x,y \, (x \le y \land y \le x \to x=y)$
③ $\forall x,y,z \, (x \le y \land y \le z \to x \le z)$
を考えます。変数$x,y,z$を集合$X$の要素とし、述語記号$\le$を関係$R$で解釈したときに、$T$の公理①〜③がすべて成り立つならば、
\[ \langle X,R \rangle \models T \]
と書いて、$\langle X,R \rangle$ は$T$のモデルであるといいます。この例では $\langle X,R \rangle$ は(半)順序集合と呼ばれます。$T$の公理がすべて一階述語論理の論理式(以下「一階の論理式」といいます)になっていることに注意してください。
ここでもし$X$が無限集合ならば、それを真に拡大する集合${}^*X$と、関係$R$を拡大する${}^*X$上の2項関係${}^*R$の組で、任意に与えられた一階の論理式$\varphi$に対して、
\[ \langle X,R \rangle \models \varphi \quad \Leftrightarrow \quad \langle {}^*X,{}^*R \rangle \models \varphi \]
が常に成り立つようなものが存在します。この ${}^*X,{}^*R$ をそれぞれ $X,R$ の超準拡大といいます。また上記の関係(一階の論理式の真偽が常に一致すること)を移行原理といいます。
先述の例で $\langle X,R \rangle$ が順序集合ならば、上記の$T$の公理は全て $\langle {}^*X,{}^*R \rangle$ でも成立しますので、$\langle {}^*X,{}^*R \rangle$ も順序集合になります。$\langle X,R \rangle$ を$T$の「標準モデル」と呼ぶならば、それに対する $\langle {}^*X,{}^*R \rangle$ は$T$の「超準モデル」と呼ばれます。
要約すると「無限集合を領域にもつどんなモデルにもそれを真に拡大する超準モデルが存在する」ということです。このことの証明はまた別記事で書くことにして、いまはまずこれを認めて先へ進みます。
さて、$R$は簡単のために2項関係としましたが、先ほども述べたように$R$は3項以上の多項関係でも、逆に1項関係でも同じことが成り立ちます。$R$が1項関係のときは $R \subseteq X$ すなわち$R$は$X$の部分集合になり、$\langle x \rangle$ が関係$R$を満たすことは $x \in R$ を意味します。このことを任意にとった$X$の部分集合 $A,B,C$ に対して適用すると、これらの超準拡大 ${}^*A,{}^*B,{}^*C$ が存在し、$\langle X,A,B,C \rangle$ と $\langle {}^*X,{}^*A,{}^*B,{}^*C \rangle$ との間で移行原理が使えますので、次のような論法が成立します。
$C=A \cup B$ とする。これは論理式で書くと、
\[ \forall x \in X \, (x \in C \leftrightarrow x \in A \lor x \in B) \]
のことである。すると移行原理によって
\[ \forall x \in {}^*X \, (x \in {}^*C \leftrightarrow x \in {}^*A \lor x \in {}^*B) \]
となるから、${}^*C={}^*A \cup {}^*B$ すなわち
\[ {}^*(A \cup B) = {}^*A \cup {}^*B \]
が成り立つ。□
同じ論法を用いることにより、
\[
{}^*(A \cap B) = {}^*A \cap {}^*B \\
{}^*(A \setminus B) = {}^*A \setminus {}^*B \\
A \subseteq B \Leftrightarrow {}^*A \subseteq {}^*B \\
{}^*(A \times B) = {}^*A \times {}^*B
\]
などが示されます(最後の式は $A \times B$ を$X$上の2項関係とみなすことで得られます)。
もう一つ、$X$上の関数についても超準拡大を考えることができます。なぜなら関数とは関係の特別なものとみなせるからです。簡単のために$f$を$X$上の1変数関数とすると、これは$X$上の2項関係であって、関数であるための条件
\[ \forall x,y,z \in X \, ( \langle x,y \rangle \in f \land \langle x,z \rangle \in f \to y=z ) \]
をみたします。すると$f$の超準拡大${}^*f$が存在して、移行原理より、
\[ \forall x,y,z \in {}^*X \, ( \langle x,y \rangle \in {}^*f \land \langle x,z \rangle \in {}^*f \to y=z ) \]
が成り立ちますから、${}^*f$は${}^*X$上の1変数関数になります。多変数関数でも全く同様です。
関数の合成に関して、
\[ {}^*(g \circ f) = {}^*g \circ {}^*f \]
が成り立つことも、移行原理を用いると簡単に示すことができます。
ここまで一般論を書きました。次はこれを実数体に適用することによって「超実数体」の議論に移ります。
(続く)(目次)
数学の知識をある程度つけた者が、超実数の世界では無限小やら無限大やらが自由に扱えることを知って、なんか面白いと思って超準解析をテキストでちゃんと勉強しようとします。するとそこには「ツェルメロ宇宙」やら「上部構造」やらのいきなり小難しい概念から始まるので、そこで萎えてしまうこともあろうかと思います。ここではもう少し簡単に、一般に数学モデルにはそれを拡大した「超準モデル」が存在することを説明し、それを実数体に適用することで「超実数体」が得られる、そして「移行原理」を駆使することで様々な性質が導ける、という順序で超準解析のサワリを紹介します。
(1) 超準モデルについて
一般に$X$を空でない集合とし、$R$を$X$上の2項関係すなわち $R \subseteq X^2$ とします。これらの対 $\langle X,R \rangle$ に対していくつかの公理系を与えると、それは一つの数学のモデルになります。$R$が3項以上の多項関係だったり、またそれらが複数個あったりしても以下の議論は同様に進められますが、簡単のためにここでは1つの2項関係だけのモデルを考えます。
例えば、述語記号$\le$を含む公理系$T$として
① $\forall x \, (x \le x)$
② $\forall x,y \, (x \le y \land y \le x \to x=y)$
③ $\forall x,y,z \, (x \le y \land y \le z \to x \le z)$
を考えます。変数$x,y,z$を集合$X$の要素とし、述語記号$\le$を関係$R$で解釈したときに、$T$の公理①〜③がすべて成り立つならば、
\[ \langle X,R \rangle \models T \]
と書いて、$\langle X,R \rangle$ は$T$のモデルであるといいます。この例では $\langle X,R \rangle$ は(半)順序集合と呼ばれます。$T$の公理がすべて一階述語論理の論理式(以下「一階の論理式」といいます)になっていることに注意してください。
ここでもし$X$が無限集合ならば、それを真に拡大する集合${}^*X$と、関係$R$を拡大する${}^*X$上の2項関係${}^*R$の組で、任意に与えられた一階の論理式$\varphi$に対して、
\[ \langle X,R \rangle \models \varphi \quad \Leftrightarrow \quad \langle {}^*X,{}^*R \rangle \models \varphi \]
が常に成り立つようなものが存在します。この ${}^*X,{}^*R$ をそれぞれ $X,R$ の超準拡大といいます。また上記の関係(一階の論理式の真偽が常に一致すること)を移行原理といいます。
先述の例で $\langle X,R \rangle$ が順序集合ならば、上記の$T$の公理は全て $\langle {}^*X,{}^*R \rangle$ でも成立しますので、$\langle {}^*X,{}^*R \rangle$ も順序集合になります。$\langle X,R \rangle$ を$T$の「標準モデル」と呼ぶならば、それに対する $\langle {}^*X,{}^*R \rangle$ は$T$の「超準モデル」と呼ばれます。
要約すると「無限集合を領域にもつどんなモデルにもそれを真に拡大する超準モデルが存在する」ということです。このことの証明はまた別記事で書くことにして、いまはまずこれを認めて先へ進みます。
さて、$R$は簡単のために2項関係としましたが、先ほども述べたように$R$は3項以上の多項関係でも、逆に1項関係でも同じことが成り立ちます。$R$が1項関係のときは $R \subseteq X$ すなわち$R$は$X$の部分集合になり、$\langle x \rangle$ が関係$R$を満たすことは $x \in R$ を意味します。このことを任意にとった$X$の部分集合 $A,B,C$ に対して適用すると、これらの超準拡大 ${}^*A,{}^*B,{}^*C$ が存在し、$\langle X,A,B,C \rangle$ と $\langle {}^*X,{}^*A,{}^*B,{}^*C \rangle$ との間で移行原理が使えますので、次のような論法が成立します。
$C=A \cup B$ とする。これは論理式で書くと、
\[ \forall x \in X \, (x \in C \leftrightarrow x \in A \lor x \in B) \]
のことである。すると移行原理によって
\[ \forall x \in {}^*X \, (x \in {}^*C \leftrightarrow x \in {}^*A \lor x \in {}^*B) \]
となるから、${}^*C={}^*A \cup {}^*B$ すなわち
\[ {}^*(A \cup B) = {}^*A \cup {}^*B \]
が成り立つ。□
同じ論法を用いることにより、
\[
{}^*(A \cap B) = {}^*A \cap {}^*B \\
{}^*(A \setminus B) = {}^*A \setminus {}^*B \\
A \subseteq B \Leftrightarrow {}^*A \subseteq {}^*B \\
{}^*(A \times B) = {}^*A \times {}^*B
\]
などが示されます(最後の式は $A \times B$ を$X$上の2項関係とみなすことで得られます)。
もう一つ、$X$上の関数についても超準拡大を考えることができます。なぜなら関数とは関係の特別なものとみなせるからです。簡単のために$f$を$X$上の1変数関数とすると、これは$X$上の2項関係であって、関数であるための条件
\[ \forall x,y,z \in X \, ( \langle x,y \rangle \in f \land \langle x,z \rangle \in f \to y=z ) \]
をみたします。すると$f$の超準拡大${}^*f$が存在して、移行原理より、
\[ \forall x,y,z \in {}^*X \, ( \langle x,y \rangle \in {}^*f \land \langle x,z \rangle \in {}^*f \to y=z ) \]
が成り立ちますから、${}^*f$は${}^*X$上の1変数関数になります。多変数関数でも全く同様です。
関数の合成に関して、
\[ {}^*(g \circ f) = {}^*g \circ {}^*f \]
が成り立つことも、移行原理を用いると簡単に示すことができます。
ここまで一般論を書きました。次はこれを実数体に適用することによって「超実数体」の議論に移ります。
(続く)(目次)



