春の近江路 GW限定パスで乗り放題の一日 [バス]
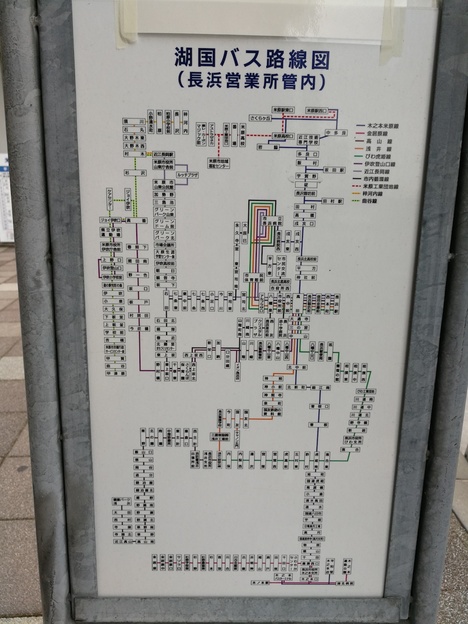
近江鉄道バスがこのゴールデンウィーク限定の乗り放題パスを出していました。1000円で近江鉄道バスと湖国バスの全路線が10日間乗り放題という破格のパスです。
というわけで連休2日目に乗ってきました。
この2箇所です。
まずは端からということで、浜大津駅から草津駅行の路線に乗ります。

乗り放題パスはバス車内でも買えます。有効期間が平成から令和までというのがまたいいです。

大津市内の旧市街を抜けてJR大津駅を経由し、東へ向かいます。


湖岸道路を抜けて近江大橋を渡ります。



イオンモール草津に立ち寄って、浜街道と呼ばれる県道を走ります。

バスはこのまま草津駅まで行きますが、乗り継ぎのため途中の下笠中央で下車します。


草津駅から来た琵琶湖博物館行のバスに乗ります。観光路線なので4列シートにかなりの乗客がいました。

通称「メロン街道」と呼ばれる農免道路を走り、途中のグリーンプラザ烏丸で下車します。


ここからは路線がつながっていないので、農道を歩いて守山市域へ向かいます。



30分弱歩いたところにある山賀のバス停から乗車し、守山駅に向かいます。



のどかな田園風景と集落を抜け、少し賑やかになったら間もなく守山駅です。

さてこの先も近江八幡方面に向かってバスを乗り継ぎたいところですが、この先は路線網がずたずたに切られており、本数も少なく歩きを入れてもうまくつながりません。あきらめて木ノ本までJR新快速でワープすることにします。
バスの時間まで余裕があるので木之本町内を散策します(駅名は木ノ本ですが町名は長浜市木之本です)。北国街道の宿場町だったので街並みに味わいがあります。


旧滋賀銀行支店だったこの建物はイベントスペースになっており、この日は北陸本線の旧線である柳ヶ瀬越えと山中越えを走るSLの貴重な映像を見せてくれました。。

木ノ本駅のすぐ近くにあるバスターミナルから、米原駅行のバスに乗ります。今では数少ない鉄道並行の国道路線です。

国道をしばらく南下します。


市街地に入って国道を離れ、長浜駅に立ち寄ります。

市立長浜病院にも立ち寄り、琵琶湖がチラッと見える県道を走り抜け、木之本から1時間以上かけて米原駅に到着です。



湖国バスの路線はコミュニティバスに移管されるなどしてかなり減りましたが、それでもまだ要所を結ぶ路線が結構残っています。これらも時間の問題かもしれません。
まだ連休は残っています。近江鉄道バスは生活路線だけではなく観光地もいくつも結んでいます。時間のある方はこのお得なパスで近江路のバス旅行はいかがでしょうか。
「路線バス歩き」のすすめ(目次)へ
というわけで連休2日目に乗ってきました。
この2箇所です。
まずは端からということで、浜大津駅から草津駅行の路線に乗ります。

乗り放題パスはバス車内でも買えます。有効期間が平成から令和までというのがまたいいです。

大津市内の旧市街を抜けてJR大津駅を経由し、東へ向かいます。


湖岸道路を抜けて近江大橋を渡ります。



イオンモール草津に立ち寄って、浜街道と呼ばれる県道を走ります。

バスはこのまま草津駅まで行きますが、乗り継ぎのため途中の下笠中央で下車します。


草津駅から来た琵琶湖博物館行のバスに乗ります。観光路線なので4列シートにかなりの乗客がいました。

通称「メロン街道」と呼ばれる農免道路を走り、途中のグリーンプラザ烏丸で下車します。


ここからは路線がつながっていないので、農道を歩いて守山市域へ向かいます。



30分弱歩いたところにある山賀のバス停から乗車し、守山駅に向かいます。



のどかな田園風景と集落を抜け、少し賑やかになったら間もなく守山駅です。

さてこの先も近江八幡方面に向かってバスを乗り継ぎたいところですが、この先は路線網がずたずたに切られており、本数も少なく歩きを入れてもうまくつながりません。あきらめて木ノ本までJR新快速でワープすることにします。
バスの時間まで余裕があるので木之本町内を散策します(駅名は木ノ本ですが町名は長浜市木之本です)。北国街道の宿場町だったので街並みに味わいがあります。


旧滋賀銀行支店だったこの建物はイベントスペースになっており、この日は北陸本線の旧線である柳ヶ瀬越えと山中越えを走るSLの貴重な映像を見せてくれました。。

木ノ本駅のすぐ近くにあるバスターミナルから、米原駅行のバスに乗ります。今では数少ない鉄道並行の国道路線です。

国道をしばらく南下します。


市街地に入って国道を離れ、長浜駅に立ち寄ります。

市立長浜病院にも立ち寄り、琵琶湖がチラッと見える県道を走り抜け、木之本から1時間以上かけて米原駅に到着です。



湖国バスの路線はコミュニティバスに移管されるなどしてかなり減りましたが、それでもまだ要所を結ぶ路線が結構残っています。これらも時間の問題かもしれません。

まだ連休は残っています。近江鉄道バスは生活路線だけではなく観光地もいくつも結んでいます。時間のある方はこのお得なパスで近江路のバス旅行はいかがでしょうか。
「路線バス歩き」のすすめ(目次)へ
わかってない奴がわかったつもりで書き留める超準解析(その10) [数学]
【超準解析について生半可な知識しかない僕が、わかったつもりの内容をちょっとずつ書き留めていきます。不正確な内容や誤りもあることをご承知ください。】
(10) アスコリ・アルツェラの定理
今回も2つの距離空間 $\langle X,d_X \rangle$ と $\langle Y,d_Y \rangle$ とその超準モデルを考えます。今回の目標は表題の定理を証明することです。
$\{ f_n \}$ を$X$の部分集合$A$から$Y$への関数列とします。アスコリ・アルツェラの定理の一つの形は次のようになります。
(アスコリ・アルツェラの定理として値域が$\mathbb{R}$のときに「一様有界」を仮定に入れた形をよく目にしますが、$\mathbb{R}$の有界閉区間はコンパクトなので【定理1】の特別な場合になっています。)
この仮定に登場する、関数列 $\{ f_n \}$ が$A$の点$x$で同程度連続とは、
\[ \forall \epsilon \in \mathbb{R}^+ \, \exists \delta \in \mathbb{R}^+ \, \forall n \in \mathbb{N} \, \forall y \in A \, (d_X(x,y) < \delta \to d_Y(f_n(x),f_n(y)) < \epsilon) \tag{1} \]
となることをいいます。$A$の任意の点で同程度連続のときは$A$上で同程度連続といいます。【定理1】を証明するために、この同程度連続という概念を超準モデル上の同値条件で表すことを考えます。
(証明)第9回【定理1】の証明とほとんど同様の手法である。まず $\{ f_n \}$ が $x \in A$ で同程度連続ならば、$(1)$と移行原理より任意の正実数$\epsilon$に対して正実数$\delta$がとれて、
\[ \forall n \in {}^*\mathbb{N} \, \forall y \in {}^*A \, ({}^*d_X(x,y) < \delta \to {}^*d_Y({}^*f_n(x),{}^*f_n(y)) < \epsilon) \tag{3} \]
とすることができる。従っていつもの考察によって$(2)$が導かれる。
逆も同様なので省略する。□
(この定理は一様収束に関する第9回【定理1】と非常によく似ていますが、それは当然であって、同程度連続とは $y \to x$ のとき$n$に関して一様収束することに他ならないからです。)
上の証明の副産物として得られた式$(3)$を用いると、次の補題が示されます。
(証明)仮定をみたす $n \in {}^*\mathbb{N}_\infty$ と任意の $x \in A$ をとる。$\{f_n\}$ が$A$上で同程度連続だから、任意の正実数$\epsilon$に対して正実数$\delta$がとれて、$(3)$より
\[ \forall y \in {}^*A \, ({}^*d_X(x,y) < \delta \to {}^*d_Y({}^*f_n(x),{}^*f_n(y)) < \epsilon /2) \]
が成り立つようにできる。従って $d_X(x,y) < \delta$ をみたす任意の $y \in A$ に対して、
\[ d_Y(f_\infty(x), f_\infty(y)) \le {}^*d_Y({}^*f_n(x), f_\infty(x)) + {}^*d_Y({}^*f_n(x), {}^*f_n(y)) + {}^*d_Y({}^*f_n(y), f_\infty(y)) \le \epsilon /2 < \epsilon \]
となる。これは$f_\infty$が$x$で連続であることを意味する。□
ちょっと脱線しますが、この補題から直ちに次が導かれます。
(証明)収束の仮定より、任意の $n \in {}^*\mathbb{N}_\infty$ と $x \in A$ について $f_\infty(x) = \mathrm{st}({}^*f_n(x))$ であるから、【補題3】より明らか。□
では、準備ができたので、本題のアスコリ・アルツェラの定理の証明に移ります。コンパクト性の同値条件については第8回【定理3】を思い出してください。
(【定理1】の証明)ある $n \in {}^*\mathbb{N}_\infty$ をとって固定する。$Y$がコンパクトだから任意の $x \in A$ に対して ${}^*f_n(x)$ は近標準点、よって
\[ f_\infty(x) = \mathrm{st}({}^*f_n(x)) \]
によって$A$から$Y$への関数$f_\infty$を定めることができ、【補題3】より$f_\infty$は$A$上で連続である。任意に $y \in {}^*A$ をとると、$A$がコンパクトだから $x = \mathrm{st}(y) \in A$ がとれ、$f_\infty$の連続性より $f_\infty(x) \approx {}^*f_\infty(y)$ である。さらに $\{f_n\}$ の同程度連続性と【定理2】より ${}^*f_n(x) \approx {}^*f_n(y)$ であり、当然 ${}^*f_n(x) \approx f_\infty(x)$ だから、
\[ {}^*f_n(y) \approx {}^*f_n(x) \approx f_\infty(x) \approx {}^*f_\infty(y) \]
より ${}^*f_n(y) \approx {}^*f_\infty(y)$ となる。$y \in {}^*A$ は任意だから第9回の表の3列目にある同値条件より、$\{f_n\}$ のある部分列が$f_\infty$に一様収束する。□
これまでの結果を組み合わせることによって、簡単に証明することができました。
これも証明を図解すると次のようになるでしょうか。
.002-7657a.jpeg)
(続く)(前記事)(目次)
(10) アスコリ・アルツェラの定理
今回も2つの距離空間 $\langle X,d_X \rangle$ と $\langle Y,d_Y \rangle$ とその超準モデルを考えます。今回の目標は表題の定理を証明することです。
$\{ f_n \}$ を$X$の部分集合$A$から$Y$への関数列とします。アスコリ・アルツェラの定理の一つの形は次のようになります。
【定理1】$A$および$Y$がともにコンパクト、かつ $\{ f_n \}$ が$A$上で同程度連続ならば、$\{f_n\}$ は一様収束する部分列をもつ。
(アスコリ・アルツェラの定理として値域が$\mathbb{R}$のときに「一様有界」を仮定に入れた形をよく目にしますが、$\mathbb{R}$の有界閉区間はコンパクトなので【定理1】の特別な場合になっています。)
この仮定に登場する、関数列 $\{ f_n \}$ が$A$の点$x$で同程度連続とは、
\[ \forall \epsilon \in \mathbb{R}^+ \, \exists \delta \in \mathbb{R}^+ \, \forall n \in \mathbb{N} \, \forall y \in A \, (d_X(x,y) < \delta \to d_Y(f_n(x),f_n(y)) < \epsilon) \tag{1} \]
となることをいいます。$A$の任意の点で同程度連続のときは$A$上で同程度連続といいます。【定理1】を証明するために、この同程度連続という概念を超準モデル上の同値条件で表すことを考えます。
【定理2】$\{ f_n \}$ が $A$の点$x$で同程度連続であることと、
\[ \forall n \in {}^*\mathbb{N} \, \forall y \in {}^*A \, (x \approx y \to {}^*f_n(x) \approx {}^*f_n(y)) \tag{2} \]
が成り立つことは同値である。
(証明)第9回【定理1】の証明とほとんど同様の手法である。まず $\{ f_n \}$ が $x \in A$ で同程度連続ならば、$(1)$と移行原理より任意の正実数$\epsilon$に対して正実数$\delta$がとれて、
\[ \forall n \in {}^*\mathbb{N} \, \forall y \in {}^*A \, ({}^*d_X(x,y) < \delta \to {}^*d_Y({}^*f_n(x),{}^*f_n(y)) < \epsilon) \tag{3} \]
とすることができる。従っていつもの考察によって$(2)$が導かれる。
逆も同様なので省略する。□
(この定理は一様収束に関する第9回【定理1】と非常によく似ていますが、それは当然であって、同程度連続とは $y \to x$ のとき$n$に関して一様収束することに他ならないからです。)
上の証明の副産物として得られた式$(3)$を用いると、次の補題が示されます。
【補題3】$\{f_n\}$ が$A$上で同程度連続で、ある $n \in {}^*\mathbb{N}_\infty$ についてすべての $x \in A$ に対する ${}^*f_n(x)$ が近標準点ならば、
\[ f_\infty(x) = \mathrm{st}({}^*f_n(x)) \]
によって定まる$A$から$Y$への関数$f_\infty$は$A$上で連続である。
(証明)仮定をみたす $n \in {}^*\mathbb{N}_\infty$ と任意の $x \in A$ をとる。$\{f_n\}$ が$A$上で同程度連続だから、任意の正実数$\epsilon$に対して正実数$\delta$がとれて、$(3)$より
\[ \forall y \in {}^*A \, ({}^*d_X(x,y) < \delta \to {}^*d_Y({}^*f_n(x),{}^*f_n(y)) < \epsilon /2) \]
が成り立つようにできる。従って $d_X(x,y) < \delta$ をみたす任意の $y \in A$ に対して、
\[ d_Y(f_\infty(x), f_\infty(y)) \le {}^*d_Y({}^*f_n(x), f_\infty(x)) + {}^*d_Y({}^*f_n(x), {}^*f_n(y)) + {}^*d_Y({}^*f_n(y), f_\infty(y)) \le \epsilon /2 < \epsilon \]
となる。これは$f_\infty$が$x$で連続であることを意味する。□
ちょっと脱線しますが、この補題から直ちに次が導かれます。
【定理4】$\{f_n\}$ が$A$上で同程度連続かつ$f_\infty$に(各点)収束するならば、$f_\infty$は$A$上で連続である。
(証明)収束の仮定より、任意の $n \in {}^*\mathbb{N}_\infty$ と $x \in A$ について $f_\infty(x) = \mathrm{st}({}^*f_n(x))$ であるから、【補題3】より明らか。□
では、準備ができたので、本題のアスコリ・アルツェラの定理の証明に移ります。コンパクト性の同値条件については第8回【定理3】を思い出してください。
(【定理1】の証明)ある $n \in {}^*\mathbb{N}_\infty$ をとって固定する。$Y$がコンパクトだから任意の $x \in A$ に対して ${}^*f_n(x)$ は近標準点、よって
\[ f_\infty(x) = \mathrm{st}({}^*f_n(x)) \]
によって$A$から$Y$への関数$f_\infty$を定めることができ、【補題3】より$f_\infty$は$A$上で連続である。任意に $y \in {}^*A$ をとると、$A$がコンパクトだから $x = \mathrm{st}(y) \in A$ がとれ、$f_\infty$の連続性より $f_\infty(x) \approx {}^*f_\infty(y)$ である。さらに $\{f_n\}$ の同程度連続性と【定理2】より ${}^*f_n(x) \approx {}^*f_n(y)$ であり、当然 ${}^*f_n(x) \approx f_\infty(x)$ だから、
\[ {}^*f_n(y) \approx {}^*f_n(x) \approx f_\infty(x) \approx {}^*f_\infty(y) \]
より ${}^*f_n(y) \approx {}^*f_\infty(y)$ となる。$y \in {}^*A$ は任意だから第9回の表の3列目にある同値条件より、$\{f_n\}$ のある部分列が$f_\infty$に一様収束する。□
これまでの結果を組み合わせることによって、簡単に証明することができました。
これも証明を図解すると次のようになるでしょうか。
.002-7657a.jpeg)
(続く)(前記事)(目次)
わかってない奴がわかったつもりで書き留める超準解析(その9) [数学]
【超準解析について生半可な知識しかない僕が、わかったつもりの内容をちょっとずつ書き留めていきます。不正確な内容や誤りもあることをご承知ください。】
(9) 距離空間上の関数列
今回も舞台は距離空間ですが、今回は2つの距離空間 $\langle X,d_X \rangle$ と $\langle Y,d_Y \rangle$ を考えます($d_X,d_Y$ はそれぞれの距離関数)。これらに対して超準モデル $\langle {}^*X,{}^*d_X \rangle$ と $\langle {}^*Y,{}^*d_Y \rangle$ を考えることができます。第3回の連続性に関する結果や第5回の数列の極限に関する結果はそのまま距離空間へ一般化できますので、それらは自由に使うこととします。
$A \subseteq X$ とし、$A$から$Y$への関数の列 $\{ f_n \}$ を考えます。これは細かく書くと $\mathbb{N} \times A$ から$Y$への2変数関数$f$を考えたうえで、$n \in \mathbb{N}$ と $x \in A$ に対して
\[ f_n(x) = f(n,x) \]
と定めることによって関数 $f_n : A \to Y$ の列を考えることになります。ここで$f$の超準拡大${}^*f$が ${}^*\mathbb{N} \times {}^*A$ から${}^*Y$への2変数関数として定まりますから、$n \in {}^*\mathbb{N}$ と $x \in {}^*A$ に対して
\[ {}^*f_n(x) = {}^*f(n,x) \]
と定めることによって関数 ${}^*f_n : {}^*A \to {}^*Y$ の列が定まり、このとき$n$は無限大超自然数の値をとることができます。
この関数列 $\{ f_n \}$ と、それとは別の関数 $f_\infty : A \to Y$ を考えたとき、関数列の収束に関して次表に示す超準モデル上の同値条件が成立します。
どうでしょうか。ほんまかいなという感じですね。特に各点収束と一様収束が$A$と${}^*A$の違いだけで表されてしまうところが注目に値するところです。順に確認してみましょう。
まず各点収束については改めて証明することはありません。第5回【数列の極限の定義】をそのまま各 $x \in A$ に対して適用しただけです。この場合 $x \in {}^*A \setminus A$ については何も言っていないことに注意して下さい。
一様収束についてはちょっと丁寧に証明してみましょう。$A$上で $\{ f_n \}$ が$f_\infty$に一様収束するとは($\epsilon - \delta$ 論法による定義で)
\[ \forall \epsilon \in \mathbb{R}^+ \, \exists L \in \mathbb{N} \, \forall n \in \mathbb{N} \, (n \ge L \to \forall x \in A \, (d_Y(f_n(x),f_\infty (x)) < \epsilon)) \]
が成り立つことをいうのでした。
(証明)$\{f_n\}$ が$f_\infty$に一様収束すると仮定する。このとき任意の正実数$\epsilon$に対しある自然数$L$が存在して、
\[ \forall n \in \mathbb{N} \, (n \ge L \to \forall x \in A \, (d_Y(f_n(x),f_\infty (x)) < \epsilon)) \]
が成り立つ。移行原理より
\[ \forall n \in {}^*\mathbb{N} \, (n \ge L \to \forall x \in {}^*A \, ({}^*d_Y({}^*f_n(x),{}^*f_\infty (x)) < \epsilon)) \]
が成り立ち、これより
\[ \forall n \in {}^*\mathbb{N}_\infty \, \forall x \in {}^*A \, ({}^*d_Y({}^*f_n(x),{}^*f_\infty (x)) < \epsilon) \]
が任意の正実数$\epsilon$に対して成り立つから、$(1)$が成り立つ。
逆に$(1)$が成り立つと仮定する。このとき任意の正実数$\epsilon$に対し、
\[ \exists L \in {}^*\mathbb{N} \, \forall n \in {}^*\mathbb{N} \, (n \ge L \to \forall x \in {}^*A \, ({}^*d_Y({}^*f_n(x),{}^*f_\infty (x)) < \epsilon)) \]
が成り立つ($L$を無限大にとればよい)。移行原理より
\[ \exists L \in \mathbb{N} \, \forall n \in \mathbb{N} \, (n \ge L \to \forall x \in A \, (d_Y(f_n(x),f_\infty (x)) < \epsilon)) \]
となり、正実数$\epsilon$は任意だから $\{f_n\}$ は$f_\infty$に一様収束する。□
これまで色々やってきた証明と同じ流れで証明できました。
3行目の一様収束する部分列が存在する条件についても、第5回【定理1】と同様の方法で証明できますので、こちらは省略します。
各点収束や一様収束が超準モデル上の簡単な同値条件で表されましたので、例えばディ二の定理が次のように証明できます。
(証明)単調性の仮定より、
\[ \forall x \in A \, \forall m,n \in \mathbb{N} \, ( m < n \to \left| f_m(x) - f_\infty (x) \right| \ge \left| f_n(x) - f_\infty (x) \right| ) \]
であるから、移行原理より
\[ \forall x \in {}^*A \, \forall m,n \in {}^*\mathbb{N} \, ( m < n \to \left| {}^*f_m(x) - {}^*f_\infty (x) \right| \ge \left| {}^*f_n(x) - {}^*f_\infty (x) \right| ) \]
が成り立つ。任意に $n \in {}^*\mathbb{N}_\infty$ と $x \in {}^*A$ をとる。$A$はコンパクトだから、第8回【定理3】より $x \approx z$ をみたす $z \in A$ がとれる(つまり$x$は近標準点で $z=\mathrm{st}(x) \in A$ となる)。各点収束の仮定より、任意の正実数$\epsilon$に対してある $m \in \mathbb{N}$ が存在して $\left| f_m(z) - f_\infty (z) \right| < \epsilon$ をみたす。$f_m$と$f_\infty$はともに$z$で連続だから ${}^*f_m(x) \approx f_m(z) \land {}^*f_\infty (x) \approx f_\infty (z)$ となって、当然 $m < n$ だから、
\[ \left| {}^*f_n(x) - {}^*f_\infty (x) \right| \le \left| {}^*f_m(x) - {}^*f_\infty (x) \right| \le \left| {}^*f_m(x) - f_m(z) \right| + \left| f_m(z) - f_\infty (z) \right| + \left| {}^*f_\infty (x) - f_\infty (z) \right| < \epsilon \]
となり、正実数$\epsilon$は任意だから ${}^*f_n(x) \approx {}^*f_\infty (x)$ である。従って【定理1】より $\{f_n\}$ は$f_\infty$に一様収束する。□
証明を図解すると次のようになるでしょうか。
.001.jpeg)
(続く)(前記事)(目次)
(9) 距離空間上の関数列
今回も舞台は距離空間ですが、今回は2つの距離空間 $\langle X,d_X \rangle$ と $\langle Y,d_Y \rangle$ を考えます($d_X,d_Y$ はそれぞれの距離関数)。これらに対して超準モデル $\langle {}^*X,{}^*d_X \rangle$ と $\langle {}^*Y,{}^*d_Y \rangle$ を考えることができます。第3回の連続性に関する結果や第5回の数列の極限に関する結果はそのまま距離空間へ一般化できますので、それらは自由に使うこととします。
$A \subseteq X$ とし、$A$から$Y$への関数の列 $\{ f_n \}$ を考えます。これは細かく書くと $\mathbb{N} \times A$ から$Y$への2変数関数$f$を考えたうえで、$n \in \mathbb{N}$ と $x \in A$ に対して
\[ f_n(x) = f(n,x) \]
と定めることによって関数 $f_n : A \to Y$ の列を考えることになります。ここで$f$の超準拡大${}^*f$が ${}^*\mathbb{N} \times {}^*A$ から${}^*Y$への2変数関数として定まりますから、$n \in {}^*\mathbb{N}$ と $x \in {}^*A$ に対して
\[ {}^*f_n(x) = {}^*f(n,x) \]
と定めることによって関数 ${}^*f_n : {}^*A \to {}^*Y$ の列が定まり、このとき$n$は無限大超自然数の値をとることができます。
この関数列 $\{ f_n \}$ と、それとは別の関数 $f_\infty : A \to Y$ を考えたとき、関数列の収束に関して次表に示す超準モデル上の同値条件が成立します。
| 距離空間上の概念 | 超準モデル上の同値条件 |
|---|---|
| $\{ f_n \}$ が$f_\infty$に各点収束 | $\forall n \in {}^*\mathbb{N}_\infty \, \forall x \in A \, ({}^*f_n(x) \approx {}^*f_\infty (x))$ |
| $\{ f_n \}$ が$f_\infty$に一様収束 | $\forall n \in {}^*\mathbb{N}_\infty \, \forall x \in {}^*A \, ({}^*f_n(x) \approx {}^*f_\infty (x))$ |
| $\{ f_n \}$ のある部分列が$f_\infty$に一様収束 | $\exists n \in {}^*\mathbb{N}_\infty \, \forall x \in {}^*A \, ({}^*f_n(x) \approx {}^*f_\infty (x))$ |
どうでしょうか。ほんまかいなという感じですね。特に各点収束と一様収束が$A$と${}^*A$の違いだけで表されてしまうところが注目に値するところです。順に確認してみましょう。
まず各点収束については改めて証明することはありません。第5回【数列の極限の定義】をそのまま各 $x \in A$ に対して適用しただけです。この場合 $x \in {}^*A \setminus A$ については何も言っていないことに注意して下さい。
一様収束についてはちょっと丁寧に証明してみましょう。$A$上で $\{ f_n \}$ が$f_\infty$に一様収束するとは($\epsilon - \delta$ 論法による定義で)
\[ \forall \epsilon \in \mathbb{R}^+ \, \exists L \in \mathbb{N} \, \forall n \in \mathbb{N} \, (n \ge L \to \forall x \in A \, (d_Y(f_n(x),f_\infty (x)) < \epsilon)) \]
が成り立つことをいうのでした。
【定理1】$A$上で $\{ f_n \}$ が$f_\infty$に一様収束することと、
\[ \forall n \in {}^*\mathbb{N}_\infty \, \forall x \in {}^*A \, ({}^*f_n(x) \approx {}^*f_\infty (x)) \tag{1} \]
が成り立つことは同値である。
(証明)$\{f_n\}$ が$f_\infty$に一様収束すると仮定する。このとき任意の正実数$\epsilon$に対しある自然数$L$が存在して、
\[ \forall n \in \mathbb{N} \, (n \ge L \to \forall x \in A \, (d_Y(f_n(x),f_\infty (x)) < \epsilon)) \]
が成り立つ。移行原理より
\[ \forall n \in {}^*\mathbb{N} \, (n \ge L \to \forall x \in {}^*A \, ({}^*d_Y({}^*f_n(x),{}^*f_\infty (x)) < \epsilon)) \]
が成り立ち、これより
\[ \forall n \in {}^*\mathbb{N}_\infty \, \forall x \in {}^*A \, ({}^*d_Y({}^*f_n(x),{}^*f_\infty (x)) < \epsilon) \]
が任意の正実数$\epsilon$に対して成り立つから、$(1)$が成り立つ。
逆に$(1)$が成り立つと仮定する。このとき任意の正実数$\epsilon$に対し、
\[ \exists L \in {}^*\mathbb{N} \, \forall n \in {}^*\mathbb{N} \, (n \ge L \to \forall x \in {}^*A \, ({}^*d_Y({}^*f_n(x),{}^*f_\infty (x)) < \epsilon)) \]
が成り立つ($L$を無限大にとればよい)。移行原理より
\[ \exists L \in \mathbb{N} \, \forall n \in \mathbb{N} \, (n \ge L \to \forall x \in A \, (d_Y(f_n(x),f_\infty (x)) < \epsilon)) \]
となり、正実数$\epsilon$は任意だから $\{f_n\}$ は$f_\infty$に一様収束する。□
これまで色々やってきた証明と同じ流れで証明できました。
3行目の一様収束する部分列が存在する条件についても、第5回【定理1】と同様の方法で証明できますので、こちらは省略します。
各点収束や一様収束が超準モデル上の簡単な同値条件で表されましたので、例えばディ二の定理が次のように証明できます。
【定理2】$A$はコンパクトとする。$A$上の実関数列 $\{f_n\}$ が$n$に伴い単調非減少または単調非増加で$f_\infty$に各点収束し、かつ各$f_n$および$f_\infty$が$A$上で連続ならば、$\{f_n\}$ の収束は一様収束である。
(証明)単調性の仮定より、
\[ \forall x \in A \, \forall m,n \in \mathbb{N} \, ( m < n \to \left| f_m(x) - f_\infty (x) \right| \ge \left| f_n(x) - f_\infty (x) \right| ) \]
であるから、移行原理より
\[ \forall x \in {}^*A \, \forall m,n \in {}^*\mathbb{N} \, ( m < n \to \left| {}^*f_m(x) - {}^*f_\infty (x) \right| \ge \left| {}^*f_n(x) - {}^*f_\infty (x) \right| ) \]
が成り立つ。任意に $n \in {}^*\mathbb{N}_\infty$ と $x \in {}^*A$ をとる。$A$はコンパクトだから、第8回【定理3】より $x \approx z$ をみたす $z \in A$ がとれる(つまり$x$は近標準点で $z=\mathrm{st}(x) \in A$ となる)。各点収束の仮定より、任意の正実数$\epsilon$に対してある $m \in \mathbb{N}$ が存在して $\left| f_m(z) - f_\infty (z) \right| < \epsilon$ をみたす。$f_m$と$f_\infty$はともに$z$で連続だから ${}^*f_m(x) \approx f_m(z) \land {}^*f_\infty (x) \approx f_\infty (z)$ となって、当然 $m < n$ だから、
\[ \left| {}^*f_n(x) - {}^*f_\infty (x) \right| \le \left| {}^*f_m(x) - {}^*f_\infty (x) \right| \le \left| {}^*f_m(x) - f_m(z) \right| + \left| f_m(z) - f_\infty (z) \right| + \left| {}^*f_\infty (x) - f_\infty (z) \right| < \epsilon \]
となり、正実数$\epsilon$は任意だから ${}^*f_n(x) \approx {}^*f_\infty (x)$ である。従って【定理1】より $\{f_n\}$ は$f_\infty$に一様収束する。□
証明を図解すると次のようになるでしょうか。
.001.jpeg)
(続く)(前記事)(目次)



