住宅地域に平日1日1往復 京阪バスの超閑散路線に乗っておく [バス]
京阪寝屋川市駅とJR四条畷駅。この2拠点を結ぶ京阪バスは、かつては経由の異なる3つの路線が走っていましたが、今は実質的には忍ケ丘駅を経由する35番系統の1路線だけになりました。
「実質的には」というのは、かつての名残の路線が平日1往復のみ運行されているからです。
それが「砂」を経由する33番系統で、昔からある伝統的な路線です。
いつなくなるか不安なので、先日乗ってきました。
朝7時台に寝屋川市駅から四条畷駅へ、夕17時台に四条畷駅から寝屋川市駅へ運行します。
今回乗ったのは四条畷駅からの便です。
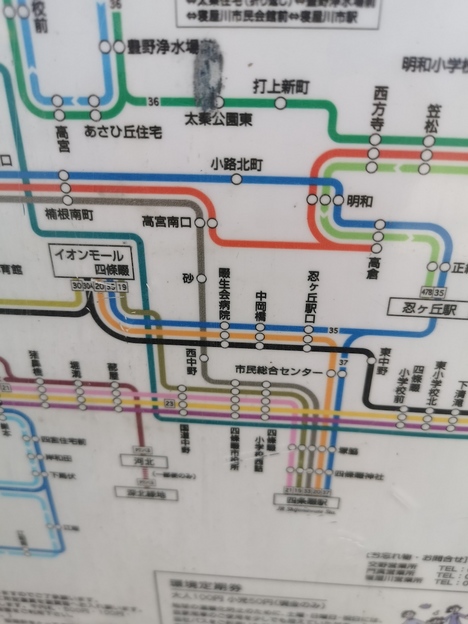
駅前広場のない四条畷駅では、狭い路上に京阪バスと近鉄バスの乗り場が並んでいます。

「砂」経由の表示がいつまで見れるのか。

駅前から170号線旧道を結ぶバス通りは一方通行の狭い道です。

170号線旧道も狭く、バスの離合も大変です。

163号線を少しだけ西に走り、また右折して170号線旧道に入ると、さらに狭い道になります。

いよいよ1日1往復しかバスが通らない「砂」を通過します。




砂停留所での乗降客はいませんでした。
寝屋川市駅まで25分のショートトリップでした。

この付近はイオンモールができてから路線がかなり再編され、砂の周辺も他の路線が近くを通るので、この路線も必要性がなくいつ突然休止されてもおかしくないですが、伝統のあるルートなので趣味的には残って欲しい気持ちがやはりあります。
「路線バス歩き」のすすめ(目次)へ
「実質的には」というのは、かつての名残の路線が平日1往復のみ運行されているからです。
それが「砂」を経由する33番系統で、昔からある伝統的な路線です。
いつなくなるか不安なので、先日乗ってきました。
朝7時台に寝屋川市駅から四条畷駅へ、夕17時台に四条畷駅から寝屋川市駅へ運行します。
今回乗ったのは四条畷駅からの便です。


駅前広場のない四条畷駅では、狭い路上に京阪バスと近鉄バスの乗り場が並んでいます。

「砂」経由の表示がいつまで見れるのか。

駅前から170号線旧道を結ぶバス通りは一方通行の狭い道です。

170号線旧道も狭く、バスの離合も大変です。

163号線を少しだけ西に走り、また右折して170号線旧道に入ると、さらに狭い道になります。

いよいよ1日1往復しかバスが通らない「砂」を通過します。




砂停留所での乗降客はいませんでした。
寝屋川市駅まで25分のショートトリップでした。

この付近はイオンモールができてから路線がかなり再編され、砂の周辺も他の路線が近くを通るので、この路線も必要性がなくいつ突然休止されてもおかしくないですが、伝統のあるルートなので趣味的には残って欲しい気持ちがやはりあります。
「路線バス歩き」のすすめ(目次)へ
Go To 長野県 [行楽]
お盆休みに、長野県の木曽地方まで旅行してきました。
1泊2日の行程で、大阪からまっすぐドライブで往復です。密になるような観光地には行ってません。コロナはバラまいていないと思いますので許してください。
中津川インターまで高速で。その先国道19号線を木曽福島まで走り、そこから山道に入っていき、木曽駒高原のホテルに宿泊です。
ホテルの部屋から見えた夕陽の御嶽山。

夕食は信州牛の鉄板焼など。

翌朝、霧が晴れたらまた別の色をした御嶽山が見えました。


木曽川を渡って反対側の開田高原へ。

開田高原から見る御嶽山はもう少し大きくて雄大です。


木曽福島へ下りて、昼食は天ざる蕎麦。

木曽川に沿ってユルユル帰路につきます。

JRの鉄橋の下から見える小野の滝。


中津川インターから高速に乗って帰宅しました。
いつもの夏に比べるとささやかな旅行ですが、久しぶりの遠出でよい気分転換になりました。
1泊2日の行程で、大阪からまっすぐドライブで往復です。密になるような観光地には行ってません。コロナはバラまいていないと思いますので許してください。
中津川インターまで高速で。その先国道19号線を木曽福島まで走り、そこから山道に入っていき、木曽駒高原のホテルに宿泊です。
ホテルの部屋から見えた夕陽の御嶽山。

夕食は信州牛の鉄板焼など。

翌朝、霧が晴れたらまた別の色をした御嶽山が見えました。


木曽川を渡って反対側の開田高原へ。

開田高原から見る御嶽山はもう少し大きくて雄大です。


木曽福島へ下りて、昼食は天ざる蕎麦。

木曽川に沿ってユルユル帰路につきます。

JRの鉄橋の下から見える小野の滝。


中津川インターから高速に乗って帰宅しました。
いつもの夏に比べるとささやかな旅行ですが、久しぶりの遠出でよい気分転換になりました。
ニュータウンの狭間の旧集落を縫って南海バスで走る [バス]
天気のよい夏の真っ盛りのお盆休みに、久しぶりの田舎路線の乗りバスをしてきました。
とはいえ昨今の状況下、遠征はやめて大阪府内の南海バスの路線です。
堺東駅を起点とし、鳳駅や栂・美木多駅を経由して和泉市内の国分峠東に至る、所要時間約1時間20分の大阪府内としてはなかなかのロングラン路線です。南北に長い堺市を縦断するのですが、南部に広がる泉北ニュータウンは通過せず、その狭間にある旧集落を縫うように走ります。
堺東駅前はさすが政令指定都市の中心駅で、駅前バスターミナルは各方面の路線が集まっています。

これから乗る路線の系統図です。停留所数もかなり多いです。


バスに乗り込むと、やはり先頭の「あほ席」や運転席の後部の席は新型コロナ対策で使用停止でした。あほ席のひとつ後ろの席が確保できたので良しとします。なお運転席は透明シートで仕切られていました。


鳳駅前までは賑やかな都市部を南西に向かって走ります。乗り降りも多いです。


JR阪和線の下をくぐると、間もなく2019年に整備された鳳駅前バスターミナルに立ち寄ります。


鳳駅を過ぎると南に向きを変え、風景も旧集落っぽい街道になります。このあたりは堺市に編入前の「福泉町」だった地域で、学校名などに福泉の名称が残っています。



泉北高速鉄道沿いに左折して、栂・美木多駅に立ち寄ります。



栂・美木多駅を過ぎるとまた旧集落に戻り、ますます田園風景になります。建設土木関係の事務所や中小工場もパラパラあります。


ちょっとした峠を越えると和泉市に入り、ほど無く終点の国分峠東に到着です。



ところでこの場所は実は3年前の2017年にも一度訪れています。その時はバス停の名前が「横山高校前」でした。調べると今年の3月1日に変更されたようで、旧名称の元になった横山高等学校はずっと以前の2008年に廃校になっていました。


でも路線図には旧名称が残っていたりして。
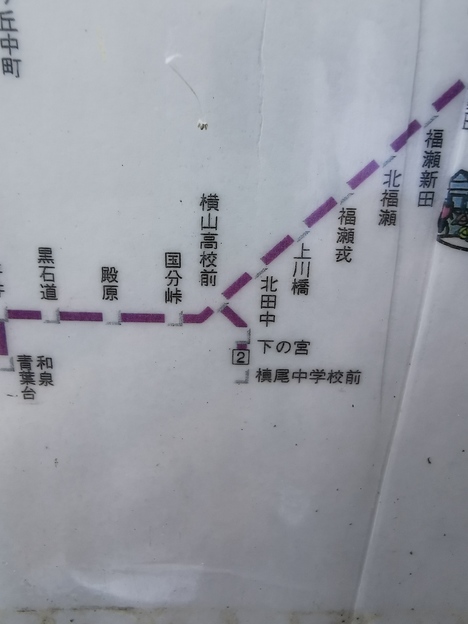
ここからは河内長野駅や和泉中央駅など各方面とバスが結んでいるのですが、今回は光明池駅行に乗って帰ることにします。

この路線も基本は旧集落沿いに走りますが、途中新興住宅地の和泉青葉台を経由します。



約25分で光明池駅に到着しました。


新型コロナが収まらない中で、なかなか乗りバス遠征ができませんが、大阪府内とはいえ久しぶりに郊外を走るバスに乗れて気分転換ができました。
「路線バス歩き」のすすめ(目次)へ
とはいえ昨今の状況下、遠征はやめて大阪府内の南海バスの路線です。
堺東駅を起点とし、鳳駅や栂・美木多駅を経由して和泉市内の国分峠東に至る、所要時間約1時間20分の大阪府内としてはなかなかのロングラン路線です。南北に長い堺市を縦断するのですが、南部に広がる泉北ニュータウンは通過せず、その狭間にある旧集落を縫うように走ります。
堺東駅前はさすが政令指定都市の中心駅で、駅前バスターミナルは各方面の路線が集まっています。

これから乗る路線の系統図です。停留所数もかなり多いです。


バスに乗り込むと、やはり先頭の「あほ席」や運転席の後部の席は新型コロナ対策で使用停止でした。あほ席のひとつ後ろの席が確保できたので良しとします。なお運転席は透明シートで仕切られていました。


鳳駅前までは賑やかな都市部を南西に向かって走ります。乗り降りも多いです。


JR阪和線の下をくぐると、間もなく2019年に整備された鳳駅前バスターミナルに立ち寄ります。


鳳駅を過ぎると南に向きを変え、風景も旧集落っぽい街道になります。このあたりは堺市に編入前の「福泉町」だった地域で、学校名などに福泉の名称が残っています。



泉北高速鉄道沿いに左折して、栂・美木多駅に立ち寄ります。



栂・美木多駅を過ぎるとまた旧集落に戻り、ますます田園風景になります。建設土木関係の事務所や中小工場もパラパラあります。


ちょっとした峠を越えると和泉市に入り、ほど無く終点の国分峠東に到着です。



ところでこの場所は実は3年前の2017年にも一度訪れています。その時はバス停の名前が「横山高校前」でした。調べると今年の3月1日に変更されたようで、旧名称の元になった横山高等学校はずっと以前の2008年に廃校になっていました。


でも路線図には旧名称が残っていたりして。

ここからは河内長野駅や和泉中央駅など各方面とバスが結んでいるのですが、今回は光明池駅行に乗って帰ることにします。

この路線も基本は旧集落沿いに走りますが、途中新興住宅地の和泉青葉台を経由します。



約25分で光明池駅に到着しました。


新型コロナが収まらない中で、なかなか乗りバス遠征ができませんが、大阪府内とはいえ久しぶりに郊外を走るバスに乗れて気分転換ができました。
「路線バス歩き」のすすめ(目次)へ
「分母の有理化」を3乗根で行う [数学]
高校数学で、平方根混じりの分数を「分母の有理化」することを習いました。
例えば次のような計算です。
\[ \frac{1}{\sqrt{2}+1} = \frac{\sqrt{2} - 1}{(\sqrt{2}+1)(\sqrt{2} - 1)} = \frac{\sqrt{2} - 1}{2 - 1} = \sqrt{2} - 1 \]
平方根混じりの分数が必ず「分母の有理化」が可能であることは、高校でちゃんと教わったかどうかは記憶にありませんが、僕自身は可能だと認識していて、面白く感じたことを覚えています。
これを説明するために、上の例を少し抽象化します。$\theta = \sqrt{2}$ とおき、多項式 $f(x)$ を
\[ f(x) = x^2 - 2 \]
とすると、$f(\theta) = 0$ となります。そして有理係数の多項式 $g(x), h(x)$ で $g(\theta) \neq 0$ となるものをとり、$\theta$混じりの分数
\[ \frac{h(\theta)}{g(\theta)} \]
を考えると、これは多項式 $g(x), h(x)$ をどう取っても「分母の有理化」が可能になるのです。なぜなら、$g(\theta) \neq 0$ の条件より $g(x)$ は $f(x)$ を因数に持たず、また $f(x)$ は有理数体$\mathbb{Q}$上でこれ以上因数分解できない(既約)ので、$f(x)$ と $g(x)$ は互いに素、よって、
\[ f(x)p(x)+g(x)q(x) = 1 \tag{1} \]
となる有理係数多項式 $p(x), q(x)$ を取ることができて、$f(\theta) = 0$ を使うと
\[ \frac{h(\theta)}{g(\theta)} = \frac{h(\theta)q(\theta)}{g(\theta)q(\theta)} = \frac{h(\theta)q(\theta)}{1 - f(\theta)p(\theta)} = h(\theta)q(\theta) \tag{2} \]
となって$\theta$混じりの有理係数多項式に変形されます。これで「分母の有理化」ができたわけです。
この抽象化をよく見ると、$\theta$はなにも平方根に限った話ではなく、有理係数多項式の根になる数(代数的数)ならば何でもよくて、3乗根でも何乗根でも、また「何乗根」で表せないようなもっと複雑な多項式の根でもいいわけです。つまり、代数的数$\theta$の(有理係数の)有理式の形で表される数は、必ず「分母の有理化」が可能ということになります。
このような一般化をした場合は、$f(x)$ は$\theta$の$\mathbb{Q}$上の「最小多項式」をとります。つまり$\theta$を根に持つ有理係数多項式で既約かつモニック(最高次係数が1)な多項式です。例えば $\theta = \sqrt[3]{2}$(2の実3乗根)ならば $f(x) = x^3 - 2$ です。
では、以下 $\theta = \sqrt[3]{2}$ と固定して、2の3乗根混じりの分数の「分母の有理化」を実際にやってみます。上の議論でこれが可能であることはわかりましたが、実際に計算するには平方根の場合のように簡単にはいきません。
まず分母の $g(x)$ が1次式 $x+a$($a$は有理数)の場合は比較的簡単です。次のように「分母の有理化」ができます。面倒なので分子の $h(x)$ は1にしてしまいましょう。
\[ \frac{1}{\theta + a} = \frac{\theta^2 - a \theta + a^2}{(\theta + a)(\theta^2 - a \theta + a^2)} = \frac{\theta^2 - a \theta + a^2}{\theta^3 + a^3} = \frac{\theta^2 - a \theta + a^2}{2 + a^3} \]
高校でも習った3次の因数分解の公式を使って「分母の有理化」ができました。
次に、$g(x)$ が2次式 $x^2+ax+b$($a,b$は有理数)の場合を考えます。残念ながらわかりやすい公式がないので、$(1)$をみたす $p(x), q(x)$ を愚直に求めることにします。ユークリッドの互除法を2段階用いてちょっと面倒な計算をして $p(x), q(x)$ を求め、$(2)$に当てはめて整理すると、次の結果になります。
\[ \frac{1}{\theta^2 + a \theta + b} = \frac{(a^2-b)\theta^2 + (2-ab)\theta +b^2-2a}{2a^3-6ab+b^3+4} \]
具体的に $a=1, b=-1$ としてこれに当てはめると、
\[ \frac{1}{\theta^2 + \theta - 1} = \frac{2\theta^2 + 3\theta -1}{11} \]
と「分母の有理化」ができました。これが本当に成り立つことは、左辺の分母と右辺の分子を掛け算して $\theta^3 = 2$ を入れると $11$ になることで確認できます。
これらの議論の一般化は、「体の拡大」という非常に奥深い内容に繋がっていて、とても面白いです。
例えば次のような計算です。
\[ \frac{1}{\sqrt{2}+1} = \frac{\sqrt{2} - 1}{(\sqrt{2}+1)(\sqrt{2} - 1)} = \frac{\sqrt{2} - 1}{2 - 1} = \sqrt{2} - 1 \]
平方根混じりの分数が必ず「分母の有理化」が可能であることは、高校でちゃんと教わったかどうかは記憶にありませんが、僕自身は可能だと認識していて、面白く感じたことを覚えています。
これを説明するために、上の例を少し抽象化します。$\theta = \sqrt{2}$ とおき、多項式 $f(x)$ を
\[ f(x) = x^2 - 2 \]
とすると、$f(\theta) = 0$ となります。そして有理係数の多項式 $g(x), h(x)$ で $g(\theta) \neq 0$ となるものをとり、$\theta$混じりの分数
\[ \frac{h(\theta)}{g(\theta)} \]
を考えると、これは多項式 $g(x), h(x)$ をどう取っても「分母の有理化」が可能になるのです。なぜなら、$g(\theta) \neq 0$ の条件より $g(x)$ は $f(x)$ を因数に持たず、また $f(x)$ は有理数体$\mathbb{Q}$上でこれ以上因数分解できない(既約)ので、$f(x)$ と $g(x)$ は互いに素、よって、
\[ f(x)p(x)+g(x)q(x) = 1 \tag{1} \]
となる有理係数多項式 $p(x), q(x)$ を取ることができて、$f(\theta) = 0$ を使うと
\[ \frac{h(\theta)}{g(\theta)} = \frac{h(\theta)q(\theta)}{g(\theta)q(\theta)} = \frac{h(\theta)q(\theta)}{1 - f(\theta)p(\theta)} = h(\theta)q(\theta) \tag{2} \]
となって$\theta$混じりの有理係数多項式に変形されます。これで「分母の有理化」ができたわけです。
この抽象化をよく見ると、$\theta$はなにも平方根に限った話ではなく、有理係数多項式の根になる数(代数的数)ならば何でもよくて、3乗根でも何乗根でも、また「何乗根」で表せないようなもっと複雑な多項式の根でもいいわけです。つまり、代数的数$\theta$の(有理係数の)有理式の形で表される数は、必ず「分母の有理化」が可能ということになります。
このような一般化をした場合は、$f(x)$ は$\theta$の$\mathbb{Q}$上の「最小多項式」をとります。つまり$\theta$を根に持つ有理係数多項式で既約かつモニック(最高次係数が1)な多項式です。例えば $\theta = \sqrt[3]{2}$(2の実3乗根)ならば $f(x) = x^3 - 2$ です。
では、以下 $\theta = \sqrt[3]{2}$ と固定して、2の3乗根混じりの分数の「分母の有理化」を実際にやってみます。上の議論でこれが可能であることはわかりましたが、実際に計算するには平方根の場合のように簡単にはいきません。
まず分母の $g(x)$ が1次式 $x+a$($a$は有理数)の場合は比較的簡単です。次のように「分母の有理化」ができます。面倒なので分子の $h(x)$ は1にしてしまいましょう。
\[ \frac{1}{\theta + a} = \frac{\theta^2 - a \theta + a^2}{(\theta + a)(\theta^2 - a \theta + a^2)} = \frac{\theta^2 - a \theta + a^2}{\theta^3 + a^3} = \frac{\theta^2 - a \theta + a^2}{2 + a^3} \]
高校でも習った3次の因数分解の公式を使って「分母の有理化」ができました。
次に、$g(x)$ が2次式 $x^2+ax+b$($a,b$は有理数)の場合を考えます。残念ながらわかりやすい公式がないので、$(1)$をみたす $p(x), q(x)$ を愚直に求めることにします。ユークリッドの互除法を2段階用いてちょっと面倒な計算をして $p(x), q(x)$ を求め、$(2)$に当てはめて整理すると、次の結果になります。
\[ \frac{1}{\theta^2 + a \theta + b} = \frac{(a^2-b)\theta^2 + (2-ab)\theta +b^2-2a}{2a^3-6ab+b^3+4} \]
具体的に $a=1, b=-1$ としてこれに当てはめると、
\[ \frac{1}{\theta^2 + \theta - 1} = \frac{2\theta^2 + 3\theta -1}{11} \]
と「分母の有理化」ができました。これが本当に成り立つことは、左辺の分母と右辺の分子を掛け算して $\theta^3 = 2$ を入れると $11$ になることで確認できます。
これらの議論の一般化は、「体の拡大」という非常に奥深い内容に繋がっていて、とても面白いです。



