吉野から熊野へ大峰山東側ルートをコミュニティバスで抜ける(その1) [バス]
ずっと課題になっていた、吉野郡の大峰山の東側を国道169号に沿って70km以上走る「R169ゆうゆうバス」に、ようやく乗ることができ、これを使って吉野町の近鉄大和上市駅から熊野市駅まで通り抜けてきました。
このルートはかつて奈良交通の「北山峡特急バス」が走っていましたが、今は廃止されて、コミュニティバスの3路線の乗り継ぎになりました。徒歩区間なしで乗り継ぐことができますが、曜日に注意が必要です。大和上市駅から下北山村までは「R169ゆうゆうバス」という長距離のコミュニティバスがありますが、1日に1往復しかなく、平日は午前に北向きで午後に南向き、土休日は逆に午前に南向きで午後に北向きという変則的な運行です。そして下北山村から和歌山県北山村の七色に抜ける下北山村営バスは平日しか走りません。どのようにしても途中下北山村内での1泊が必要ですが、今回は日曜日から月曜日にかけての1泊2日とし、泊地の下北山村でゆっくり時間を取ることにしました。
【1日目】大阪阿部野橋→大和上市→下桑原→(徒歩)→寺垣内→池原大橋
早朝に大阪を出発し、大和上市駅で8:30発のゆうゆうバスに乗ります。運行は奈良交通です。



このバスの運賃は通常なら大和上市から終点の下桑原まで2900円ですが、事前に下北山村役場へ申込書を郵送して「地域公共交通パスポート」と「特別乗車証」を入手すると、1000円で乗車することができます(下北山村内での乗降が条件)。乗車証に乗降区間を記入し、後車時にパスポートを見せて乗車証と現金1000円を渡す方式です。

吉野川沿いに国道169号をひたすら南下して行きます。



川上村に入るとまもなく大滝ダムが見え、それを超えるとダム湖沿いの道になります。



ほどなく「湯盛温泉杉の湯」に到着し、ここで20分トイレ休憩です。ホテルと道の駅があります。


大和上市駅からここまでは川上村営の「やまぶきバス」もあるのですが、土休日には運行しません。

他には春から秋にかけて、大和八木駅から大台ヶ原に行くバスがここを経由します。出発時にちょうど入れ替わりになるように遭遇しました。
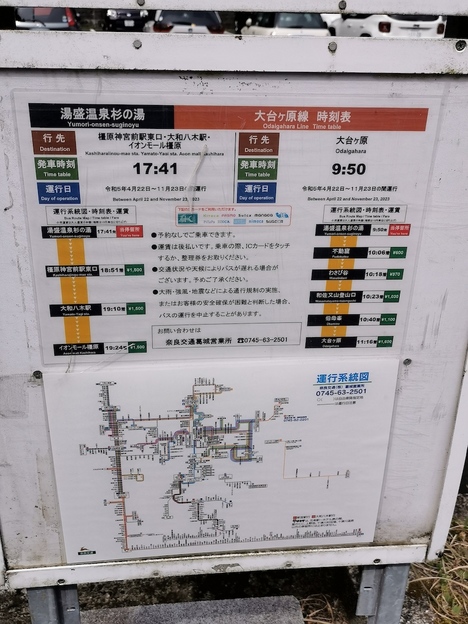

吉野川に沿って坂道を登っていき、ループ橋を超えると、トンネルの手前で大台ヶ原ドライブウェイと分岐します。




分水嶺の新伯母峯トンネルを越えて上北山村に入ると、熊野灘に注ぐ北山川に沿って下って行きます。
両側の山が高く深い谷です。




大きなダム湖の池原貯水池沿いにしばらく走り、下北山村に入るとまもなく池原ダムが見えます。



最後は国道169号を離れて国道425号に入り、下北山村の中心地を通り抜けると、終点の下桑原です。
ここまで約2時間40分のロングラン乗車です。運転手さんもお疲れ様です。




周囲は商店は何もないですが、ちょっとした公園と公衆トイレがあるので助かります。大阪で買ってきたコンビニ弁当をここで食べました。
バスは川沿いの空き地で折り返しまで休憩です。


今夜の宿泊は温泉のある池原地区で、ここからはかなり距離があるので、役場のある寺垣内地区まで川沿いを歩き、そこからまた戻りのゆうゆうバスに乗って池原地区まで行くことにします。



橿原まで95km。同じ奈良県でも遠くまで来たものです。


郵便局や村役場のある寺垣内まで来ましたが、ここまで休憩できるカフェなどはなく、ひたすら川と山を眺めて歩くだけです。いつもはこれくらいの距離は平気なのですが、今回はどういうわけか4kmくらいから腰が痛くて歩くのが非常に辛くなってしまいました。バス停に椅子があったのが幸いです。



寺垣内から戻りのゆうゆうバスに乗って、池原大橋で下車し、少し歩いて宿泊地に行きます。




温泉で痛めた腰を温め、そこの食堂で鹿肉と豚肉の合い挽きハンバーグの定食を食べました。

(その2)へ続く
「路線バス歩き」のすすめ(目次)へ
このルートはかつて奈良交通の「北山峡特急バス」が走っていましたが、今は廃止されて、コミュニティバスの3路線の乗り継ぎになりました。徒歩区間なしで乗り継ぐことができますが、曜日に注意が必要です。大和上市駅から下北山村までは「R169ゆうゆうバス」という長距離のコミュニティバスがありますが、1日に1往復しかなく、平日は午前に北向きで午後に南向き、土休日は逆に午前に南向きで午後に北向きという変則的な運行です。そして下北山村から和歌山県北山村の七色に抜ける下北山村営バスは平日しか走りません。どのようにしても途中下北山村内での1泊が必要ですが、今回は日曜日から月曜日にかけての1泊2日とし、泊地の下北山村でゆっくり時間を取ることにしました。
【1日目】大阪阿部野橋→大和上市→下桑原→(徒歩)→寺垣内→池原大橋
早朝に大阪を出発し、大和上市駅で8:30発のゆうゆうバスに乗ります。運行は奈良交通です。



このバスの運賃は通常なら大和上市から終点の下桑原まで2900円ですが、事前に下北山村役場へ申込書を郵送して「地域公共交通パスポート」と「特別乗車証」を入手すると、1000円で乗車することができます(下北山村内での乗降が条件)。乗車証に乗降区間を記入し、後車時にパスポートを見せて乗車証と現金1000円を渡す方式です。

吉野川沿いに国道169号をひたすら南下して行きます。



川上村に入るとまもなく大滝ダムが見え、それを超えるとダム湖沿いの道になります。



ほどなく「湯盛温泉杉の湯」に到着し、ここで20分トイレ休憩です。ホテルと道の駅があります。


大和上市駅からここまでは川上村営の「やまぶきバス」もあるのですが、土休日には運行しません。

他には春から秋にかけて、大和八木駅から大台ヶ原に行くバスがここを経由します。出発時にちょうど入れ替わりになるように遭遇しました。


吉野川に沿って坂道を登っていき、ループ橋を超えると、トンネルの手前で大台ヶ原ドライブウェイと分岐します。




分水嶺の新伯母峯トンネルを越えて上北山村に入ると、熊野灘に注ぐ北山川に沿って下って行きます。
両側の山が高く深い谷です。




大きなダム湖の池原貯水池沿いにしばらく走り、下北山村に入るとまもなく池原ダムが見えます。



最後は国道169号を離れて国道425号に入り、下北山村の中心地を通り抜けると、終点の下桑原です。
ここまで約2時間40分のロングラン乗車です。運転手さんもお疲れ様です。




周囲は商店は何もないですが、ちょっとした公園と公衆トイレがあるので助かります。大阪で買ってきたコンビニ弁当をここで食べました。
バスは川沿いの空き地で折り返しまで休憩です。



今夜の宿泊は温泉のある池原地区で、ここからはかなり距離があるので、役場のある寺垣内地区まで川沿いを歩き、そこからまた戻りのゆうゆうバスに乗って池原地区まで行くことにします。



橿原まで95km。同じ奈良県でも遠くまで来たものです。


郵便局や村役場のある寺垣内まで来ましたが、ここまで休憩できるカフェなどはなく、ひたすら川と山を眺めて歩くだけです。いつもはこれくらいの距離は平気なのですが、今回はどういうわけか4kmくらいから腰が痛くて歩くのが非常に辛くなってしまいました。バス停に椅子があったのが幸いです。



寺垣内から戻りのゆうゆうバスに乗って、池原大橋で下車し、少し歩いて宿泊地に行きます。




温泉で痛めた腰を温め、そこの食堂で鹿肉と豚肉の合い挽きハンバーグの定食を食べました。

(その2)へ続く
「路線バス歩き」のすすめ(目次)へ
呉から福山まで瀬戸内の島づたいにほぼバスで横断する [バス]
ゴールデンウィークに入ったので、乗りバス遠征に出かけました。
今回は瀬戸内海の島々をほぼバスでアイランドホッピングです。
呉市の広地区から南東方向の瀬戸内海に、安芸灘諸島と呼ばれる島々が並んでいます。ここに現在は7つの橋がかけられていて、大崎下島までは路線バス、その先の岡村島まで徒歩で行くことができます。岡村島から大三島の間だけ船に乗ると、その先はしまなみ海道を使って福山までバスで行けます。合計11個もの島を渡るこのルートを呉から福山まで横断してきました。
前日に早めのスカイレール葬式鉄を済ませて呉駅付近で宿泊し、朝からJRで広に移動します。

安芸灘諸島との間を結ぶ瀬戸内産交バスは、区間便と合わせて大体1時間に1本の運行です。
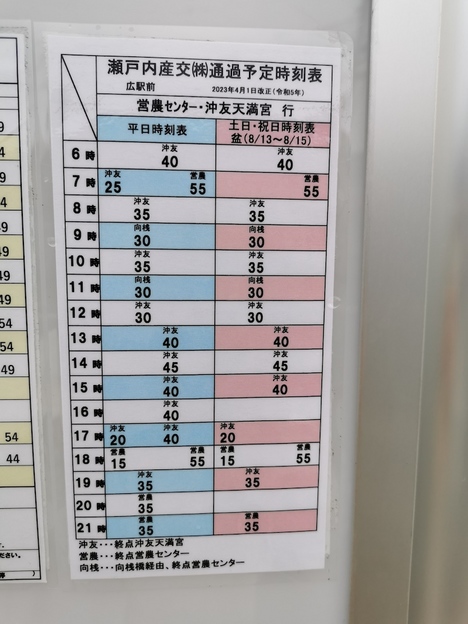

まずは安芸灘大橋を渡って下蒲刈島へ。




続いて蒲刈大橋を渡って上蒲刈島へ。


海が見える蒲刈支所前で一旦バスを降ります。
旧蒲刈町役場だった呉市蒲刈支所と、瀬戸内産交の本社があります。



海を見ながらホゲホゲしてから、約1時間後のバスに乗ります。今度は途中の営農センター前までの区間便なので、終点で下車します。



静かな漁港ですが、感じのいいカフェがあったのでお茶休憩しました。


またバスに乗り、豊島大橋を渡って豊島へ、続いて豊浜大橋を渡って大崎下島に入ります。





バスは大崎下島までしか行きませんので、その先の島へ渡る橋の手前の初崎で下車しました。
ここから岡村島まで歩きます。


このルートは「とびしま海道」と名付けられているそうです。サイクリングにちょうどよさそうな道で、実際に自転車の人たちをたくさん見ました。
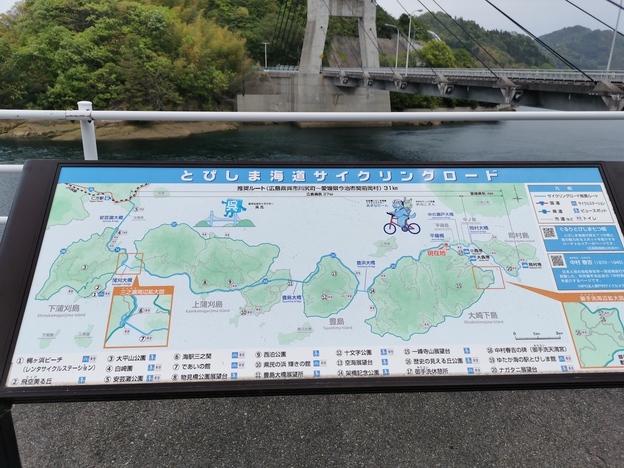
平羅島、中ノ島という2つの小さな島を橋伝いに通り抜けると・・・



いよいよ岡村島に渡る岡村大橋です。


なぜ「いよいよ」と気合が入るかというと、この先は伊予の国・・・広島県と愛媛県を結ぶ県境の橋だからです。
橋のまん中には県境を示す標示が描かれています。


例によって360度写真を撮りました(マウスを乗せてグリグリ回してください)。

愛媛県の岡村島に上陸です。



ここから海岸沿いに約40分ほど歩くと、岡村港に到着です。



ちょっと歩き疲れたので、港のそばの食堂で魚定食をいただきました。

岡村港からは大三島や今治までフェリーがそこそこ出ています。今回は大三島の宗方港まで乗船します。


デッキから下大下島、大下島、柏島や、北側の大崎上島を眺めて、宗方港に到着です。
朝から曇っていた天気がだんだん晴れてきて、いい景色になりました。




船を降りると瀬戸内海交通のバスが待っていますので、これに乗って宮浦港まで行きます。




宮浦港には瀬戸内海交通の本社があり、ここから今治や松山方面行の高速バスが出ています。
本州方面行のバスはここからは出ていないので、まずは今治行に乗ってインター近くの大三島BSまで行きます。





大三島BSの近くには、多々羅大橋が眺められる道の駅があるので、そこで土産を買ってから、福山行のしまなみリーディングの高速バスに乗りました。



ここからは西瀬戸自動車道(しまなみ海道)に乗り、生口島、因島、向島を通り抜けて、新尾道大橋を渡って本州に上陸します。




夕刻に無事福山駅に到着しました。

瀬戸内海は本当にたくさんの島が並んでおり、橋でつながっている島も多いので、色んなルートで島伝いに移動することができて楽しいです。今回のルートがこのようにほぼバスで繋がることを知った時は目から鱗でした。
「路線バス歩き」のすすめ(目次)へ
今回は瀬戸内海の島々をほぼバスでアイランドホッピングです。
呉市の広地区から南東方向の瀬戸内海に、安芸灘諸島と呼ばれる島々が並んでいます。ここに現在は7つの橋がかけられていて、大崎下島までは路線バス、その先の岡村島まで徒歩で行くことができます。岡村島から大三島の間だけ船に乗ると、その先はしまなみ海道を使って福山までバスで行けます。合計11個もの島を渡るこのルートを呉から福山まで横断してきました。
前日に早めのスカイレール葬式鉄を済ませて呉駅付近で宿泊し、朝からJRで広に移動します。

安芸灘諸島との間を結ぶ瀬戸内産交バスは、区間便と合わせて大体1時間に1本の運行です。


まずは安芸灘大橋を渡って下蒲刈島へ。




続いて蒲刈大橋を渡って上蒲刈島へ。


海が見える蒲刈支所前で一旦バスを降ります。
旧蒲刈町役場だった呉市蒲刈支所と、瀬戸内産交の本社があります。



海を見ながらホゲホゲしてから、約1時間後のバスに乗ります。今度は途中の営農センター前までの区間便なので、終点で下車します。



静かな漁港ですが、感じのいいカフェがあったのでお茶休憩しました。


またバスに乗り、豊島大橋を渡って豊島へ、続いて豊浜大橋を渡って大崎下島に入ります。





バスは大崎下島までしか行きませんので、その先の島へ渡る橋の手前の初崎で下車しました。
ここから岡村島まで歩きます。


このルートは「とびしま海道」と名付けられているそうです。サイクリングにちょうどよさそうな道で、実際に自転車の人たちをたくさん見ました。

平羅島、中ノ島という2つの小さな島を橋伝いに通り抜けると・・・



いよいよ岡村島に渡る岡村大橋です。


なぜ「いよいよ」と気合が入るかというと、この先は伊予の国・・・広島県と愛媛県を結ぶ県境の橋だからです。
橋のまん中には県境を示す標示が描かれています。


例によって360度写真を撮りました(マウスを乗せてグリグリ回してください)。

愛媛県の岡村島に上陸です。



ここから海岸沿いに約40分ほど歩くと、岡村港に到着です。



ちょっと歩き疲れたので、港のそばの食堂で魚定食をいただきました。

岡村港からは大三島や今治までフェリーがそこそこ出ています。今回は大三島の宗方港まで乗船します。



デッキから下大下島、大下島、柏島や、北側の大崎上島を眺めて、宗方港に到着です。
朝から曇っていた天気がだんだん晴れてきて、いい景色になりました。




船を降りると瀬戸内海交通のバスが待っていますので、これに乗って宮浦港まで行きます。




宮浦港には瀬戸内海交通の本社があり、ここから今治や松山方面行の高速バスが出ています。
本州方面行のバスはここからは出ていないので、まずは今治行に乗ってインター近くの大三島BSまで行きます。





大三島BSの近くには、多々羅大橋が眺められる道の駅があるので、そこで土産を買ってから、福山行のしまなみリーディングの高速バスに乗りました。



ここからは西瀬戸自動車道(しまなみ海道)に乗り、生口島、因島、向島を通り抜けて、新尾道大橋を渡って本州に上陸します。




夕刻に無事福山駅に到着しました。

瀬戸内海は本当にたくさんの島が並んでおり、橋でつながっている島も多いので、色んなルートで島伝いに移動することができて楽しいです。今回のルートがこのようにほぼバスで繋がることを知った時は目から鱗でした。
「路線バス歩き」のすすめ(目次)へ
河内平野を南北に縦断 分断間近の通貫路線を乗り通す [バス]
大阪のバスマニアにはよく知られた(大阪府内としては)長大路線として、近鉄バスの萱島線(萱島〜近鉄八尾駅前)があります。河内平野を南北に縦断する約17kmの路線で、大阪市内から放射状に走る各鉄道路線に直交するフィーダー輸送の役割を担っています。
この路線が、2023年6月1日より朝夕の一部を除いて、JR住道で系統分割されることが発表されました。
(近鉄バス公式リリース)【6/1より】萱島線の運行計画を変更いたします。
もともとこの路線の萱島〜JR住道間は需要が少ないようで、ここ数年間はダイヤ変更の度に減便が繰り返されてきており、現時点では萱島〜近鉄八尾駅前の通し便は1時間に1〜2程度しかなく、残りはJR住道〜近鉄八尾駅前の区間運行便となっています。経由する府道21号線がよく渋滞するので定時運行が難しく、今回の系統分割に至ったようです。
(以前にも萱島〜荒本駅前とJR住道〜近鉄八尾駅前の2系統に分割していた時期がありましたが、2006年以降は全線通しが復活していました。)
この路線は以前より何回か乗車していましたが、改めて全線通し便に名残乗車することとしました。
近鉄八尾駅前からは続けて藤井寺行に乗車し、合計2路線で北河内から南河内までのバス縦断です。
高架ホームに神社の神木が貫く京阪萱島駅からスタートです。

駅から少し離れた道路上にある萱島バス停から、近鉄八尾駅前行に乗ります。

府道149号線を南下し、少しだけ東に向きを変えて、巣本交差点からは府道21号線を南下していきます。


テレビでも紹介された、特徴ある看板のアウトレット家具店の横を通ります。

かつて梅田と産業大学前を直通していた阪奈生駒線との乗換停留所だった赤井を過ぎ、住之井橋で寝屋川を渡った後、府道を離れて一旦JR住道駅南側のロータリーに立ち寄ります。



府道21号線に戻って少し南下すると、広い国道308号線を西に向かい、近鉄荒本駅前に立ち寄ります。



かつて上本町と石切神社前を直通していた枚岡線との乗換停留所だった菱江を通ります。昔は東西にも近鉄バスの長大路線がいくつかありましたが、全て廃止されています。

奈良線の若江岩田駅前には、府道21号線上のバス停でのアクセスです。


西郡新町からは斜めに左折し府道21号線を外れ、萱振付近ではかなり狭い道になります。



昼間の便は、アリオ八尾ショッピングセンターの広場に入ります。

アリオ八尾を過ぎると、すぐに終点の近鉄八尾駅前です。通し運賃の340円は、6月からの系統分割後もICカードで乗り継げばそのまま変わりません。



そのまま藤井寺駅行のバスに乗り継ぎます。今回はリバイバル旧塗色車でした。


乗客が多かったため正面窓の写真は撮れず、左窓からの写真になります。
八尾の旧市街地を抜けて、JR八尾駅前を通り過ぎ、踏切を渡ります。



ここからは基本的に府道2号線(旧道)を南下していきます。
八尾空港への入口を通ります。


地下鉄八尾南駅前に立ち寄り、大正橋で大和川を渡ります。

小山で右折し西に向かうと、まもなく藤井寺駅に到着です。



京阪本線萱島駅から近鉄南大阪線藤井寺駅まで2路線を繋いで、途中6つの鉄道駅に接続しながら乗りバス縦断しました。
長大系統はやはり非効率なので分割はやむを得ませんが、路線自体は鉄道網を補完するのでこれからも残っていてほしいです。
「路線バス歩き」のすすめ(目次)へ
この路線が、2023年6月1日より朝夕の一部を除いて、JR住道で系統分割されることが発表されました。
(近鉄バス公式リリース)【6/1より】萱島線の運行計画を変更いたします。
もともとこの路線の萱島〜JR住道間は需要が少ないようで、ここ数年間はダイヤ変更の度に減便が繰り返されてきており、現時点では萱島〜近鉄八尾駅前の通し便は1時間に1〜2程度しかなく、残りはJR住道〜近鉄八尾駅前の区間運行便となっています。経由する府道21号線がよく渋滞するので定時運行が難しく、今回の系統分割に至ったようです。
(以前にも萱島〜荒本駅前とJR住道〜近鉄八尾駅前の2系統に分割していた時期がありましたが、2006年以降は全線通しが復活していました。)
この路線は以前より何回か乗車していましたが、改めて全線通し便に名残乗車することとしました。
近鉄八尾駅前からは続けて藤井寺行に乗車し、合計2路線で北河内から南河内までのバス縦断です。
高架ホームに神社の神木が貫く京阪萱島駅からスタートです。

駅から少し離れた道路上にある萱島バス停から、近鉄八尾駅前行に乗ります。


府道149号線を南下し、少しだけ東に向きを変えて、巣本交差点からは府道21号線を南下していきます。


テレビでも紹介された、特徴ある看板のアウトレット家具店の横を通ります。

かつて梅田と産業大学前を直通していた阪奈生駒線との乗換停留所だった赤井を過ぎ、住之井橋で寝屋川を渡った後、府道を離れて一旦JR住道駅南側のロータリーに立ち寄ります。



府道21号線に戻って少し南下すると、広い国道308号線を西に向かい、近鉄荒本駅前に立ち寄ります。



かつて上本町と石切神社前を直通していた枚岡線との乗換停留所だった菱江を通ります。昔は東西にも近鉄バスの長大路線がいくつかありましたが、全て廃止されています。

奈良線の若江岩田駅前には、府道21号線上のバス停でのアクセスです。


西郡新町からは斜めに左折し府道21号線を外れ、萱振付近ではかなり狭い道になります。



昼間の便は、アリオ八尾ショッピングセンターの広場に入ります。

アリオ八尾を過ぎると、すぐに終点の近鉄八尾駅前です。通し運賃の340円は、6月からの系統分割後もICカードで乗り継げばそのまま変わりません。



そのまま藤井寺駅行のバスに乗り継ぎます。今回はリバイバル旧塗色車でした。


乗客が多かったため正面窓の写真は撮れず、左窓からの写真になります。
八尾の旧市街地を抜けて、JR八尾駅前を通り過ぎ、踏切を渡ります。



ここからは基本的に府道2号線(旧道)を南下していきます。
八尾空港への入口を通ります。


地下鉄八尾南駅前に立ち寄り、大正橋で大和川を渡ります。

小山で右折し西に向かうと、まもなく藤井寺駅に到着です。



京阪本線萱島駅から近鉄南大阪線藤井寺駅まで2路線を繋いで、途中6つの鉄道駅に接続しながら乗りバス縦断しました。
長大系統はやはり非効率なので分割はやむを得ませんが、路線自体は鉄道網を補完するのでこれからも残っていてほしいです。
「路線バス歩き」のすすめ(目次)へ
近江八幡〜三雲 春の湖南路をバスと徒歩で結ぶ [バス]
ようやく暖かくなったので、久しぶりの徒歩混じり乗りバスに出かけました。
滋賀県のJR琵琶湖線近江八幡駅からJR草津線三雲駅までを結ぶルートです。
このルート、かつては近江八幡駅と三雲駅を国鉄バス→西日本JRバスが直接結んでいました。JRバスが撤退した後、現在は竜王町より北側は近江鉄道バス、南側は湖南市コミュニティバスが路線を維持しています。今回、かつてのJRバスのルートを辿っていくつもりでしたが、事前の調査を怠ったため、近江鉄道バスの部分で間違った路線に乗ってしまいました。
近江八幡駅の北口から岡屋南行に乗ります。本来JRバスの後継路線は南口から出る竜王ダイハツ前行なのですが、同じ竜王町方面へ行くバスということで間違えてしまいました。

いったん西向きに進んで近江八幡市街を抜け、南へ向きを変えてJR琵琶湖線と新幹線をくぐると、田園地帯が広がります。



少しだけ国道8号線を西向きに走り、日野川を越えて竜王町に入ると、また南に向きを変えて県道を進んでいきます。


田んぼの中にフレンドマートと一緒に建つ竜王町役場に立ち寄って、集落の中の狭い道を抜けていきます。


「ダイハツ車 岡屋の里の 希望乗せ」と書かれた看板を横目に南西に曲がり、ダイハツ工業西門の前を過ぎると、ほどなく終点の岡屋南に着きます。



ここから湖南市方面に少し歩きます。天気はいいのですが、国道477号線はやや交通量が多く歩きにくいので、途中から川沿いの脇道に入ります。


春の小川といった感じの気持ちのいい散歩道です。



下田口まで来ると、三雲駅行の湖南市コミュニティバスのバス停があります。時間があるのでこのあたりをもう少し散歩することにします。


この付近には、中山団地というちょっとしたニュータウンがあります。駅から離れているので交通手段はほぼマイカーだと思われます。


それでも団地の中まで一応コミュニティバスが走っています。ちょうど来た甲西駅行のバスは、誰も乗り降りせずに通り過ぎていきました。

団地を後にして県道沿いの喫茶店で昼食を取り、三雲駅行の犬顔をしたバスに乗ります。


工業団地沿いの広い県道をまっすぐ南下し、にごり池を越えて集落に入ると、まもなく三雲駅に到着です。




三雲駅は南口に湖南市や甲賀市のコミュニティバスが発着する広い駅前広場ができており、かつて国鉄バスがひしめきあって発着していた北口は、駐車場とタクシー乗り場だけになっていました。


JR草津線で帰ります。

国鉄→JRバスの跡を辿れなかったのは残念(間抜け)ですが、そのかわり春の気持ちのいい気候の中で歩いたり、下田地区のニュータウンを探訪できたりしたので、楽しい1日でした。
「路線バス歩き」のすすめ(目次)へ
滋賀県のJR琵琶湖線近江八幡駅からJR草津線三雲駅までを結ぶルートです。
このルート、かつては近江八幡駅と三雲駅を国鉄バス→西日本JRバスが直接結んでいました。JRバスが撤退した後、現在は竜王町より北側は近江鉄道バス、南側は湖南市コミュニティバスが路線を維持しています。今回、かつてのJRバスのルートを辿っていくつもりでしたが、事前の調査を怠ったため、近江鉄道バスの部分で間違った路線に乗ってしまいました。
近江八幡駅の北口から岡屋南行に乗ります。本来JRバスの後継路線は南口から出る竜王ダイハツ前行なのですが、同じ竜王町方面へ行くバスということで間違えてしまいました。


いったん西向きに進んで近江八幡市街を抜け、南へ向きを変えてJR琵琶湖線と新幹線をくぐると、田園地帯が広がります。



少しだけ国道8号線を西向きに走り、日野川を越えて竜王町に入ると、また南に向きを変えて県道を進んでいきます。


田んぼの中にフレンドマートと一緒に建つ竜王町役場に立ち寄って、集落の中の狭い道を抜けていきます。


「ダイハツ車 岡屋の里の 希望乗せ」と書かれた看板を横目に南西に曲がり、ダイハツ工業西門の前を過ぎると、ほどなく終点の岡屋南に着きます。



ここから湖南市方面に少し歩きます。天気はいいのですが、国道477号線はやや交通量が多く歩きにくいので、途中から川沿いの脇道に入ります。


春の小川といった感じの気持ちのいい散歩道です。



下田口まで来ると、三雲駅行の湖南市コミュニティバスのバス停があります。時間があるのでこのあたりをもう少し散歩することにします。


この付近には、中山団地というちょっとしたニュータウンがあります。駅から離れているので交通手段はほぼマイカーだと思われます。


それでも団地の中まで一応コミュニティバスが走っています。ちょうど来た甲西駅行のバスは、誰も乗り降りせずに通り過ぎていきました。


団地を後にして県道沿いの喫茶店で昼食を取り、三雲駅行の犬顔をしたバスに乗ります。


工業団地沿いの広い県道をまっすぐ南下し、にごり池を越えて集落に入ると、まもなく三雲駅に到着です。




三雲駅は南口に湖南市や甲賀市のコミュニティバスが発着する広い駅前広場ができており、かつて国鉄バスがひしめきあって発着していた北口は、駐車場とタクシー乗り場だけになっていました。


JR草津線で帰ります。

国鉄→JRバスの跡を辿れなかったのは残念(間抜け)ですが、そのかわり春の気持ちのいい気候の中で歩いたり、下田地区のニュータウンを探訪できたりしたので、楽しい1日でした。
「路線バス歩き」のすすめ(目次)へ
天理〜上野市 今月限りの名阪国道バス乗り継ぎ [バス]
かつて、三重交通と奈良交通が共同で、名阪国道を経由する天理駅〜上野市駅の都市間バスを運行していました。この路線はその後、途中の針インターと国道山添で乗り継ぎとなる3路線に分割されましたが、両区間を路線バスだけで移動できるルートとして残ってきました。
しかし、この3月末で奈良交通が真ん中の針インター〜国道山添の路線を廃止することになり、4月からはバスでの乗り継ぎ移動が不可になってしまうので、名残の乗車をしてきました。
ルートはこちら。ついでに山添村コミュニティバスで山添村から名張駅までの乗車もしてきました。
天理駅前の奈良交通路線図と時刻表。現時点でも針インター〜国道山添間は平日しか走りませんが、これが4月からは完全に廃止となります。
天理駅11:18発の針インター行に乗車します。新型コロナ対策でずっと座れなかった通称「あほ席」が解禁になっていました。


天理市内を少し走ってから、名阪国道に乗ります。


速度違反の車にバンバン抜かされながら、「Ωカーブ」を登坂車線でゆっくり走ります。名阪国道は高速道路ではないので、客席にシートベルトはありません。


本線上にある国道福住と国道針のバス停。まだこの区間のバス停はしばらく残ります。


ドライブイン施設のある針インターに到着しました。乗継時間が1分しかないので慌ただしいなと思ったら、なんとそのまま同じバスで国道山添行になり、乗換せずに先へ行くことができました(どの便もそうなのかは知りません)。


下道を少し走って山辺高校に立ち寄ります。ここまでは4月以降も残る路線です。
山辺高校はバスが他に3台待機していました。


ここからはいよいよ廃止される区間です。


奈良市(旧都祁村)から山添村に突入。途中のバス停も3月末限りです。



山添インターを降りて、終点の国道山添に到着です。



5分ほど遅れて到着したので次の三重交通バスへの乗継時間が3分しかなく、しかもバス停の場所が国道を挟んだ反対側にあるのでちょっと焦りました。僕はこの場所には数年前に一度来ていたので迷わずにすみましたが、初めての人は運転手さんに聞いておかないと混乱すると思います。

治田インターまでは下道「非名阪」を走り、その先は名阪国道です。


大内インター付近に1年前まであったドライブインは、すっかり更地になっていました。

12:58に上野市駅に到着しました。乗り継ぎが良いので所要時間は1時間40分、運賃は合計2,080円です。同じ区間を電車なら11:28出発で13:03に到着(近鉄+伊賀鉄道)で所要時間1時間35分、運賃は1,270円(4月からは近鉄の値上げで1,440円)なので、値段は割高ですが乗換が少なく楽という意味では悪くない交通機関だったと思います。

さて、上野公園で少々時間をつぶし、桑町までちょっとだけ伊賀鉄道に乗って……



また同じ三重交通バスで国道山添に戻ります。


さっき時間がなくて見れなかった、国道山添バス停の時刻表をじっくり見ることにします。
奈良交通の針インター行。これは標柱ごと無くなるのでしょう。



同じ場所にある三重交通の高速バス梅田・新大阪行は、2021年1月から運休中です。復活しないのでしょうか。

少し歩いて、山添村役場のある大西から、今度は山添村コミュニティバスに乗って名張駅に向かいます。これも平日だけの運行です。


運転席との間は透明シートが貼られていて、前面展望はダメでした。写真は全部左側の窓越しです。


カーブの多い峠を越えて、名張川沿いに走ります。



桔梗が丘の住宅地と、名張の旧市街地を抜けていきます。


名張駅前の広場に入るのかと思ったら、駅から3分ほど離れた駐車場まで連れて行かれました。




携帯の電池が尽きそうなので、コンセントのあるアーバンライナーに乗って帰ります。

天理駅〜上野市駅の名阪国道バスルートは、3月31日までの平日ならまだ乗車できます。名阪国道を一般路線バスでぶち抜くのも味わいありますので、乗りたくなった方はお急ぎください。
「路線バス歩き」のすすめ(目次)へ
しかし、この3月末で奈良交通が真ん中の針インター〜国道山添の路線を廃止することになり、4月からはバスでの乗り継ぎ移動が不可になってしまうので、名残の乗車をしてきました。
ルートはこちら。ついでに山添村コミュニティバスで山添村から名張駅までの乗車もしてきました。
天理駅前の奈良交通路線図と時刻表。現時点でも針インター〜国道山添間は平日しか走りませんが、これが4月からは完全に廃止となります。

天理駅11:18発の針インター行に乗車します。新型コロナ対策でずっと座れなかった通称「あほ席」が解禁になっていました。


天理市内を少し走ってから、名阪国道に乗ります。


速度違反の車にバンバン抜かされながら、「Ωカーブ」を登坂車線でゆっくり走ります。名阪国道は高速道路ではないので、客席にシートベルトはありません。


本線上にある国道福住と国道針のバス停。まだこの区間のバス停はしばらく残ります。


ドライブイン施設のある針インターに到着しました。乗継時間が1分しかないので慌ただしいなと思ったら、なんとそのまま同じバスで国道山添行になり、乗換せずに先へ行くことができました(どの便もそうなのかは知りません)。


下道を少し走って山辺高校に立ち寄ります。ここまでは4月以降も残る路線です。
山辺高校はバスが他に3台待機していました。


ここからはいよいよ廃止される区間です。


奈良市(旧都祁村)から山添村に突入。途中のバス停も3月末限りです。



山添インターを降りて、終点の国道山添に到着です。



5分ほど遅れて到着したので次の三重交通バスへの乗継時間が3分しかなく、しかもバス停の場所が国道を挟んだ反対側にあるのでちょっと焦りました。僕はこの場所には数年前に一度来ていたので迷わずにすみましたが、初めての人は運転手さんに聞いておかないと混乱すると思います。

治田インターまでは下道「非名阪」を走り、その先は名阪国道です。


大内インター付近に1年前まであったドライブインは、すっかり更地になっていました。

12:58に上野市駅に到着しました。乗り継ぎが良いので所要時間は1時間40分、運賃は合計2,080円です。同じ区間を電車なら11:28出発で13:03に到着(近鉄+伊賀鉄道)で所要時間1時間35分、運賃は1,270円(4月からは近鉄の値上げで1,440円)なので、値段は割高ですが乗換が少なく楽という意味では悪くない交通機関だったと思います。

さて、上野公園で少々時間をつぶし、桑町までちょっとだけ伊賀鉄道に乗って……



また同じ三重交通バスで国道山添に戻ります。


さっき時間がなくて見れなかった、国道山添バス停の時刻表をじっくり見ることにします。
奈良交通の針インター行。これは標柱ごと無くなるのでしょう。



同じ場所にある三重交通の高速バス梅田・新大阪行は、2021年1月から運休中です。復活しないのでしょうか。

少し歩いて、山添村役場のある大西から、今度は山添村コミュニティバスに乗って名張駅に向かいます。これも平日だけの運行です。


運転席との間は透明シートが貼られていて、前面展望はダメでした。写真は全部左側の窓越しです。


カーブの多い峠を越えて、名張川沿いに走ります。



桔梗が丘の住宅地と、名張の旧市街地を抜けていきます。


名張駅前の広場に入るのかと思ったら、駅から3分ほど離れた駐車場まで連れて行かれました。




携帯の電池が尽きそうなので、コンセントのあるアーバンライナーに乗って帰ります。

天理駅〜上野市駅の名阪国道バスルートは、3月31日までの平日ならまだ乗車できます。名阪国道を一般路線バスでぶち抜くのも味わいありますので、乗りたくなった方はお急ぎください。
「路線バス歩き」のすすめ(目次)へ
ウカシェビッチの公理系から全トートロジーが証明可能なことを証明する(勉強ノート) [数学]
命題論理において、最小限の公理系によって形式化された体系として、ポーランドのヤン・ウカシェビッチが考案した公理系が知られています。この体系を使うと、命題論理の全てのトートロジー(恒真式)が形式的に証明できます。面白そうだったので自分で実際にやってみましたが、あまり簡単ではなくパズルみたいな面白さがありましたので、本記事ではこれを一通り紹介します。
1. 論理式と形式的証明の定義
まず、本記事における論理式を次で定義します。
以下、論理式の記述において、カッコは紛れがない限り省略し、論理演算子 $\lnot, \to$ の結合は $\lnot$ が $\to$ より強いものとします。例えば $\lnot A \to B$ は正式には $(\lnot (A)) \to (B)$ のことです。
一般の論理体系では他に $\lor, \land, \leftrightarrow$ といった論理演算子も使われますが、本記事ではこれらは略記法とみなします。つまり、
i) $A \lor B$ は $\lnot A \to B$ の略記
ii) $A \land B$ は $\lnot(A \to \lnot B)$ の略記
iii) $A \leftrightarrow B$ は $(A \to B) \land (B \to A)$ の略記
とします。本記事では最後までこれらの論理演算子は使わず、$\lnot$ と $\to$ だけで突っ走ります。
次に、論理の公理を定義します。ウカシェビッチの公理系といわれるものです。
これらを使って、次によって形式的証明が定義されます。
この定義の iii) で、「$B_j$ と $B_j \to B_i$ から $B_i$ を推論すること」が形式的証明における推論規則として定められています。この推論規則をモーダス・ポーネンスといい、以下「MP」と略記します。本記事で使う推論規則はMPだけです。
このように定義した形式的証明と、体系を外から取り扱う(メタ理論としての)証明は、ごっちゃになると紛らわしいので本記事では言葉を使い分けます。
2. いろいろな論理の定理の形式的証明
この体系でいろいろな論理式が論理の定理であることの形式的証明が得られます。公理の種類が少ないだけにその形式的証明はいささかトリッキーです。
まず最初に、一見あたりまえのような次の論理式を形式的に証明します。
(証明)
次は $A \to A$ の形式的証明である。各行の頭の (a),(b),…は識別記号であり、: の右側の記述は形式的証明に使われた根拠を表す。
□
このように、形式的証明をまじめにやると意外と手間がかかります。そこで、少しでも手間を省く強力な手法である演繹定理を先に証明します。
(証明)
$(2)$から$(1)$はMPより明らかなので、$(1)$から$(2)$を証明する。$(1)$より $\Sigma \cup \{A\}$ から $B$ への形式的証明となる論理式の列 $C_1, C_2, \cdots, C_{n-1}, B$ がある。形式的証明の長さ $n$ に関する帰納法を用いる。すなわち、$C_i \ (i < n)$ については全て $\Sigma \vdash A \to C_i$ であると仮定する。形式的証明の定義から $B$ について場合分けする。
i) $B$ が $\Sigma$ の要素(前提)、または論理の公理[A1] $\sim$ [A3]のいずれかのとき:
次は $\Sigma$ からの $A \to B$ の形式的証明である。
ii) $B$ が $A$ のとき:
[T1] が論理の定理だから $\vdash A \to A$ すなわち $\vdash A \to B$ である。
iii) $B$ がある $C_i, C_j \ (i,j < n)$ からMPによって得られるとき、すなわち $C_j$ が $C_i \to B$ のとき:
帰納法の仮定より $\Sigma \vdash A \to C_i$ かつ $\Sigma \vdash A \to (C_i \to B)$ である。従ってこれらの形式的証明となる論理式の列を連結し、それに次の論理式の列を追加することにより、$\Sigma$ からの $A \to B$ の形式的証明が得られる。
以上より全ての場合について$(2)$が示された。
□
演繹定理を利用すると、以下次々と論理の定理が形式的に証明できます。
(証明)
[T2] 演繹定理より $\{ \lnot A \} \vdash A \to B$ を示せばよい。
[T3] $\{ \lnot \lnot A \} \vdash A$ を示せばよい。
[T4]
[T5] $\{ A \to (B \to C), B, A \} \vdash C$ を示せばよい。
[T6] $\{ A \to B, B \to C, A \} \vdash C$ を示せばよい。
[T7] $\{ \lnot A \to A \} \vdash A$ を示せばよい。
[T8] $\{ A \to B, \lnot A \to B \} \vdash B$ を示せばよい。
[T9] $\{ A \to B \} \vdash \lnot B \to \lnot A$ を示せばよい。
[T10] $\{ A \} \vdash \lnot B \to \lnot(A \to B)$ を示せばよい。
□
このようにして、論理の定理がいくらでも形式的に証明できますが、キリがないのでここでやめておきます。
3. トートロジーが形式的証明可能なことの証明
ここまでの議論では、論理演算子 $\lnot, \to$ や推論規則には何の意味もなく、形式的証明はただ記号列を規則に従って並べているだけでした。これから論理演算子に意味を持たせ、論理式の真偽を定義します。
トートロジーを言い換えると、原始命題の真理値をどのように割り当てても真になる論理式ということです。定義から具体的に検証することによって、論理の公理 [A1] $\sim$ [A3] は全てトートロジーになることが分かります。
このように論理式に真偽の意味を持たせると、形式的証明が次の定理によって意味づけされます。
(証明)
$\Sigma \vdash A$ かつ $\Sigma$ の要素が全て真とする。$\Sigma$ から $A$ への形式的証明を $B_1, B_2, \cdots, B_{n-1}, A$ とし、$i < n$ に対して定理が成り立つ、すなわち $\Sigma \models B_i \ (i < n)$ であると仮定すると、$B_i \ (i < n)$ は全て真である。
i) $A$ が $\Sigma$ の要素のとき:
明らかに $A$ は真である。
ii) $A$ が [A1] $\sim$ [A3] のいずれかのとき:
[A1] $\sim$ [A3] はどれもトートロジーだから、やはり $A$ は真 である。
iii) ある $B_i, B_j \ (i,j < n)$ に対して $B_j$ が $B_i \to A$ のとき:
$B_i$ が真、かつ $B_i \to A$ が真 であるから、【定義7】iii) より $A$ は真でなければならない。
以上より全ての場合で $A$ が真であるから、形式的証明の長さ $n$ に関する帰納法によって $\Sigma \models A$ が示された。
□
つまり「形式的に証明できれば論理的に正しい」と言って良いわけです。これによって、論理の定理は前提なしで形式的に証明できるので、全てトートロジーです。
逆に、トートロジーが全て形式的に証明できること、すなわち論理の定理であることの証明に進みます。準備として、論理式の真理値と形式的証明の関係がよくわかる次の補題を証明します。
(証明)
論理式 $A$ の構成に関する帰納法を用いる。
i) $A$ が原始命題 $P$ のとき:
(a) $P$ が真のとき $A$ は真である。このとき $\{ P \} \vdash P$ は自明だから $\{ P \} \vdash A$ となり、$(3)$が成立する。
(b) $P$ が偽のとき $A$ は偽である。このとき $\{ \lnot P \} \vdash \lnot P$ は自明だから $\{ \lnot P \} \vdash \lnot A$ となり、$(4)$が成立する。
ii) $A$ が $\lnot B$ で、$B$ について補題が成立するとき:
(a) $P_1, \cdots , P_m$ が真、$P_{m+1}, \cdots , P_n$ が偽のときに $A$ が真ならば、このとき $B$ は偽であるから、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash \lnot B
\end{equation*}
である。$\lnot B$ は $A$ だから$(3)$が成立する。
(b) $P_1, \cdots , P_m$ が真、$P_{m+1}, \cdots , P_n$ が偽のときに $A$ が偽ならば、このとき $B$ は真であるから、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash B
\end{equation*}
であり、さらに [T4] より $\vdash B \to \lnot \lnot B$ だから、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash \lnot \lnot B
\end{equation*}
である。$\lnot B$ は $A$ だから$(4)$が成立する。
iii) $A$ が $B \to C$ で、$B$ と $C$ について補題が成立するとき:
(a) $P_1, \cdots , P_m$ が真、$P_{m+1}, \cdots , P_n$ が偽のときに $A$ が真ならば、このとき $B$ が偽であるか、または $C$ が真である。
$B$ が偽の場合は、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash \lnot B
\end{equation*}
であり、さらに [T2] より $\vdash \lnot B \to (B \to C)$ だから、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash B \to C
\end{equation*}
である。$B \to C$ は $A$ だから$(3)$が成立する。
$C$ が真の場合は、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash C
\end{equation*}
であり、さらに [A1] より $\vdash C \to (B \to C)$ だから、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash B \to C
\end{equation*}
である。$B \to C$ は $A$ だから$(3)$が成立する。
(b) $P_1, \cdots , P_m$ が真、$P_{m+1}, \cdots , P_n$ が偽のときに $A$ が偽ならば、このとき $B$ が真かつ $C$ が偽であるから、
\begin{eqnarray*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} &\vdash& B \\
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} &\vdash& \lnot C
\end{eqnarray*}
であり、さらに [T10] より $\vdash B \to (\lnot C \to \lnot (B \to C))$ だから、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash \lnot (B \to C)
\end{equation*}
である。$B \to C$ は $A$ だから$(4)$が成立する。
以上より、全ての論理式 $A$ に対して補題が証明できた。
□
この補題を使って、本記事の目的である次の定理を証明します。
(証明)
$\models A$ とする。$A$ を構成する原始命題を全て取り出し $P_1, P_2, \cdots , P_n$ とすると、これらの真理値がどのように割り当てられても $A$ は真である。特に $P_n$ に注目すると、【補題10】より、
\begin{eqnarray*}
\{ P_1, \cdots , P_{n-1}, P_n \} &\vdash& A \\
\{ P_1, \cdots , P_{n-1}, \lnot P_n \} &\vdash& A
\end{eqnarray*}
である。これから演繹定理より、
\begin{eqnarray*}
\{ P_1, \cdots , P_{n-1} \} &\vdash& P_n \to A \\
\{ P_1, \cdots , P_{n-1} \} &\vdash& \lnot P_n \to A
\end{eqnarray*}
となる。一方 [T8] より、
\begin{equation*}
\vdash (P_n \to A) \to ((\lnot P_n \to A) \to A)
\end{equation*}
であるから、
\begin{equation*}
\{ P_1, \cdots , P_{n-2}, P_{n-1} \} \vdash A
\end{equation*}
が得られる。同様に、
\begin{eqnarray*}
\{ P_1, \cdots , P_{n-2}, \lnot P_{n-1}, P_n \} &\vdash& A \\
\{ P_1, \cdots , P_{n-2}, \lnot P_{n-1}, \lnot P_n \} &\vdash& A
\end{eqnarray*}
から
\begin{equation*}
\{ P_1, \cdots , P_{n-2}, \lnot P_{n-1} \} \vdash A
\end{equation*}
が得られる。従って、
\begin{eqnarray*}
\{ P_1, \cdots , P_{n-2}, P_{n-1} \} \vdash A \\
\{ P_1, \cdots , P_{n-2}, \lnot P_{n-1} \} \vdash A
\end{eqnarray*}
である。以下この操作を次々繰り返すと、最終的に
\begin{equation*}
\vdash A
\end{equation*}
が得られる。
□
たった3種類の公理系と1つの推論規則から全てのトートロジーが形式的に証明できることが、これで確認できました。
1. 論理式と形式的証明の定義
まず、本記事における論理式を次で定義します。
【定義1】(論理式)記号の集合として、原始命題と呼ばれる無限個の記号 $P_1 \ P_2 \ \cdots$ と、論理演算子と呼ばれる2個の記号 $\lnot \ \to$ およびカッコ $( \ )$ がある。このとき、次によって帰納的に定まる記号の列を論理式と呼ぶ。
i) 原始命題 $P_1, P_2, \cdots$ はそれぞれ論理式である。
ii) $A$ が論理式ならば $\lnot (A)$ は論理式である。
iii) $A, B$ が論理式ならば $(A) \to (B)$ は論理式である。
iv) 以上で定義されるものだけが論理式である。
i) 原始命題 $P_1, P_2, \cdots$ はそれぞれ論理式である。
ii) $A$ が論理式ならば $\lnot (A)$ は論理式である。
iii) $A, B$ が論理式ならば $(A) \to (B)$ は論理式である。
iv) 以上で定義されるものだけが論理式である。
以下、論理式の記述において、カッコは紛れがない限り省略し、論理演算子 $\lnot, \to$ の結合は $\lnot$ が $\to$ より強いものとします。例えば $\lnot A \to B$ は正式には $(\lnot (A)) \to (B)$ のことです。
一般の論理体系では他に $\lor, \land, \leftrightarrow$ といった論理演算子も使われますが、本記事ではこれらは略記法とみなします。つまり、
i) $A \lor B$ は $\lnot A \to B$ の略記
ii) $A \land B$ は $\lnot(A \to \lnot B)$ の略記
iii) $A \leftrightarrow B$ は $(A \to B) \land (B \to A)$ の略記
とします。本記事では最後までこれらの論理演算子は使わず、$\lnot$ と $\to$ だけで突っ走ります。
次に、論理の公理を定義します。ウカシェビッチの公理系といわれるものです。
【定義2】(論理の公理)$A,B,C$ が任意の論理式のとき、次の3種類の論理式を論理の公理という。
[A1] $A \to (B \to A)$
[A2] $(A \to (B \to C)) \to ((A \to B) \to (A \to C))$
[A3] $(\lnot B \to \lnot A) \to (A \to B)$
[A1] $A \to (B \to A)$
[A2] $(A \to (B \to C)) \to ((A \to B) \to (A \to C))$
[A3] $(\lnot B \to \lnot A) \to (A \to B)$
これらを使って、次によって形式的証明が定義されます。
【定義3】(形式的証明)$\Sigma$を論理式の集合、$A$ を論理式とする。論理式の有限個の列 $B_1, B_2, \cdots, B_{n-1}, B_n$ があり、$B_n$ が $A$ であって、かつ各々の $B_i$ が、
i) $\Sigma$ の要素である。
ii) 論理の公理 [A1] $\sim$ [A3] のいずれかである。
iii) ある $B_j, B_k \ (j,k < i)$ があって、$B_k$ が $B_j \to B_i$ となっている。
のいずれかをみたすとき、$A$ は $\Sigma$ から形式的証明可能といい、 \begin{equation*} \Sigma \vdash A \end{equation*} と書く。このとき、論理式の列 $B_1, B_2, \cdots, B_{n-1}, A$ を 「$\Sigma$ からの $A$ の形式的証明」といい、$\Sigma$ の要素となる論理式を前提、$A$ を結論という。
$\Sigma$ が空集合のとき、$\Sigma \vdash A$ を $\vdash A$ と書き、このとき $A$ を論理の定理という。
i) $\Sigma$ の要素である。
ii) 論理の公理 [A1] $\sim$ [A3] のいずれかである。
iii) ある $B_j, B_k \ (j,k < i)$ があって、$B_k$ が $B_j \to B_i$ となっている。
のいずれかをみたすとき、$A$ は $\Sigma$ から形式的証明可能といい、 \begin{equation*} \Sigma \vdash A \end{equation*} と書く。このとき、論理式の列 $B_1, B_2, \cdots, B_{n-1}, A$ を 「$\Sigma$ からの $A$ の形式的証明」といい、$\Sigma$ の要素となる論理式を前提、$A$ を結論という。
$\Sigma$ が空集合のとき、$\Sigma \vdash A$ を $\vdash A$ と書き、このとき $A$ を論理の定理という。
この定義の iii) で、「$B_j$ と $B_j \to B_i$ から $B_i$ を推論すること」が形式的証明における推論規則として定められています。この推論規則をモーダス・ポーネンスといい、以下「MP」と略記します。本記事で使う推論規則はMPだけです。
このように定義した形式的証明と、体系を外から取り扱う(メタ理論としての)証明は、ごっちゃになると紛らわしいので本記事では言葉を使い分けます。
2. いろいろな論理の定理の形式的証明
この体系でいろいろな論理式が論理の定理であることの形式的証明が得られます。公理の種類が少ないだけにその形式的証明はいささかトリッキーです。
まず最初に、一見あたりまえのような次の論理式を形式的に証明します。
【定理4】$A$ を任意の論理式とする。次の論理式は論理の定理である。
[T1] $A \to A$
[T1] $A \to A$
(証明)
次は $A \to A$ の形式的証明である。各行の頭の (a),(b),…は識別記号であり、: の右側の記述は形式的証明に使われた根拠を表す。
| (a) | $A \to ((A \to A) \to A)$ | : [A1] |
| (b) | $(A \to ((A \to A) \to A)) \to ((A \to (A \to A)) \to (A \to A))$ | : [A2] |
| (c) | $(A \to (A \to A)) \to (A \to A)$ | : (a),(b),MP |
| (d) | $A \to (A \to A)$ | : [A1] |
| (e) | $A \to A$ | : (d),(c),MP |
□
このように、形式的証明をまじめにやると意外と手間がかかります。そこで、少しでも手間を省く強力な手法である演繹定理を先に証明します。
【定理5】(演繹定理)$\Sigma$を論理式の集合、$A, B$ を論理式とするとき、
\begin{equation} \tag{1}
\Sigma \cup \{A\} \vdash B
\end{equation}
であることと、
\begin{equation} \tag{2}
\Sigma \vdash A \to B
\end{equation}
であることとは同値である。
(証明)
$(2)$から$(1)$はMPより明らかなので、$(1)$から$(2)$を証明する。$(1)$より $\Sigma \cup \{A\}$ から $B$ への形式的証明となる論理式の列 $C_1, C_2, \cdots, C_{n-1}, B$ がある。形式的証明の長さ $n$ に関する帰納法を用いる。すなわち、$C_i \ (i < n)$ については全て $\Sigma \vdash A \to C_i$ であると仮定する。形式的証明の定義から $B$ について場合分けする。
i) $B$ が $\Sigma$ の要素(前提)、または論理の公理[A1] $\sim$ [A3]のいずれかのとき:
次は $\Sigma$ からの $A \to B$ の形式的証明である。
| (a) | $B$ | : 前提または論理の公理 |
| (b) | $B \to (A \to B)$ | : [A1] |
| (c) | $A \to B$ | : (a),(b),MP |
ii) $B$ が $A$ のとき:
[T1] が論理の定理だから $\vdash A \to A$ すなわち $\vdash A \to B$ である。
iii) $B$ がある $C_i, C_j \ (i,j < n)$ からMPによって得られるとき、すなわち $C_j$ が $C_i \to B$ のとき:
帰納法の仮定より $\Sigma \vdash A \to C_i$ かつ $\Sigma \vdash A \to (C_i \to B)$ である。従ってこれらの形式的証明となる論理式の列を連結し、それに次の論理式の列を追加することにより、$\Sigma$ からの $A \to B$ の形式的証明が得られる。
| (a) | $(A \to (C_i \to B)) \to ((A \to C_i) \to (A \to B))$ | : [A2] |
| (b) | $(A \to C_i) \to (A \to B)$ | : $A \to (C_i \to B)$, (a), MP |
| (c) | $A \to B$ | : $A \to C_i$, (b), MP |
以上より全ての場合について$(2)$が示された。
□
演繹定理を利用すると、以下次々と論理の定理が形式的に証明できます。
【定理6】$A,B,C$ を任意の論理式とする。次の各々は論理の定理である。
[T2] $\lnot A \to (A \to B)$
[T3] $\lnot \lnot A \to A$
[T4] $A \to \lnot \lnot A$
[T5] $(A \to (B \to C)) \to (B \to (A \to C))$
[T6] $(A \to B) \to ((B \to C) \to (A \to C))$
[T7] $(\lnot A \to A) \to A$
[T8] $(A \to B) \to ((\lnot A \to B) \to B)$
[T9] $(A \to B) \to (\lnot B \to \lnot A)$
[T10] $A \to (\lnot B \to \lnot(A \to B))$
[T2] $\lnot A \to (A \to B)$
[T3] $\lnot \lnot A \to A$
[T4] $A \to \lnot \lnot A$
[T5] $(A \to (B \to C)) \to (B \to (A \to C))$
[T6] $(A \to B) \to ((B \to C) \to (A \to C))$
[T7] $(\lnot A \to A) \to A$
[T8] $(A \to B) \to ((\lnot A \to B) \to B)$
[T9] $(A \to B) \to (\lnot B \to \lnot A)$
[T10] $A \to (\lnot B \to \lnot(A \to B))$
(証明)
[T2] 演繹定理より $\{ \lnot A \} \vdash A \to B$ を示せばよい。
| (a) | $\lnot A$ | : 前提 |
| (b) | $\lnot A \to (\lnot B \to \lnot A)$ | : [A1] |
| (c) | $\lnot B \to \lnot A$ | : (a),(b),MP |
| (d) | $(\lnot B \to \lnot A) \to (A \to B)$ | : [A3] |
| (e) | $A \to B$ | : (c),(d),MP |
[T3] $\{ \lnot \lnot A \} \vdash A$ を示せばよい。
| (a) | $\lnot \lnot A$ | : 前提 |
| (b) | $\lnot \lnot A \to (\lnot A \to \lnot \lnot \lnot A)$ | : [T2] |
| (c) | $\lnot A \to \lnot \lnot \lnot A$ | : (a),(b),MP |
| (d) | $(\lnot A \to \lnot \lnot \lnot A) \to (\lnot \lnot A \to A)$ | : [A3] |
| (e) | $\lnot \lnot A \to A$ | : (c),(d),MP |
| (f) | $A$ | : (a),(e),MP |
[T4]
| (a) | $\lnot \lnot \lnot A \to \lnot A$ | : [T3] |
| (b) | $(\lnot \lnot \lnot A \to \lnot A) \to (A \to \lnot \lnot A)$ | : [A3] |
| (c) | $A \to \lnot \lnot A$ | : (a),(b),MP |
[T5] $\{ A \to (B \to C), B, A \} \vdash C$ を示せばよい。
| (a) | $A$ | : 前提 |
| (b) | $A \to (B \to C)$ | : 前提 |
| (c) | $B \to C$ | : (a),(b),MP |
| (d) | $B$ | : 前提 |
| (e) | $C$ | : (d),(c),MP |
[T6] $\{ A \to B, B \to C, A \} \vdash C$ を示せばよい。
| (a) | $A$ | : 前提 |
| (b) | $A \to B$ | : 前提 |
| (c) | $B$ | : (a),(b),MP |
| (d) | $B \to C$ | : 前提 |
| (e) | $C$ | : (c),(d),MP |
[T7] $\{ \lnot A \to A \} \vdash A$ を示せばよい。
| (a) | $\lnot A \to (A \to \lnot (A \to A))$ | : [T2] |
| (b) | $(\lnot A \to (A \to \lnot (A \to A))) \to ((\lnot A \to A) \to (\lnot A \to \lnot (A \to A)))$ | : [A2] |
| (c) | $(\lnot A \to A) \to (\lnot A \to \lnot (A \to A))$ | : (a),(b),MP |
| (d) | $\lnot A \to A$ | : 前提 |
| (e) | $\lnot A \to \lnot (A \to A)$ | : (d),(c),MP |
| (f) | $(\lnot A \to \lnot (A \to A)) \to ((A \to A) \to A)$ | : [A3] |
| (g) | $(A \to A) \to A$ | : (e),(f),MP |
| (h) | $A \to A$ | : [T1] |
| (i) | $A$ | : (h),(g),MP |
[T8] $\{ A \to B, \lnot A \to B \} \vdash B$ を示せばよい。
| (a) | $\lnot A \to B$ | : 前提 |
| (b) | $(\lnot A \to B) \to ((B \to \lnot \lnot B) \to (\lnot A \to \lnot \lnot B))$ | : [T6] |
| (c) | $(B \to \lnot \lnot B) \to (\lnot A \to \lnot \lnot B)$ | : (a),(b),MP |
| (d) | $B \to \lnot \lnot B$ | : [T4] |
| (e) | $\lnot A \to \lnot \lnot B$ | : (d),(c),MP |
| (f) | $(\lnot A \to \lnot \lnot B) \to (\lnot B \to A)$ | : [A3] |
| (g) | $\lnot B \to A$ | : (e),(f),MP |
| (h) | $(\lnot B \to A) \to ((A \to B) \to (\lnot B \to B))$ | : [T6] |
| (i) | $(A \to B) \to (\lnot B \to B)$ | : (g),(h),MP |
| (j) | $A \to B$ | : 前提 |
| (k) | $\lnot B \to B$ | : (j),(i),MP |
| (l) | $(\lnot B \to B) \to B$ | : [T7] |
| (m) | $B$ | : (k),(l),MP |
[T9] $\{ A \to B \} \vdash \lnot B \to \lnot A$ を示せばよい。
| (a) | $A \to B$ | : 前提 |
| (b) | $(A \to B) \to ((B \to \lnot \lnot B) \to (A \to \lnot \lnot B))$ | : [T6] |
| (c) | $(B \to \lnot \lnot B) \to (A \to \lnot \lnot B)$ | : (a),(b),MP |
| (d) | $B \to \lnot \lnot B$ | : [T4] |
| (e) | $A \to \lnot \lnot B$ | : (d),(c),MP |
| (f) | $\lnot \lnot A \to A$ | : [T3] |
| (g) | $(\lnot \lnot A \to A) \to ((A \to \lnot \lnot B) \to (\lnot \lnot A \to \lnot \lnot B))$ | : [T6] |
| (h) | $(A \to \lnot \lnot B) \to (\lnot \lnot A \to \lnot \lnot B)$ | : (f),(g),MP |
| (i) | $\lnot \lnot A \to \lnot \lnot B$ | : (e),(h),MP |
| (j) | $(\lnot \lnot A \to \lnot \lnot B) \to (\lnot B \to \lnot A)$ | : [A3] |
| (k) | $\lnot B \to \lnot A$ | : (i),(j),MP |
[T10] $\{ A \} \vdash \lnot B \to \lnot(A \to B)$ を示せばよい。
| (a) | $(A \to B) \to (A \to B)$ | : [T1] |
| (b) | $((A \to B) \to (A \to B)) \to (A \to ((A \to B) \to B))$ | : [T5] |
| (c) | $A \to ((A \to B) \to B)$ | : (a),(b),MP |
| (d) | $A$ | : 前提 |
| (e) | $(A \to B) \to B$ | : (d),(c),MP |
| (f) | $((A \to B) \to B) \to (\lnot B \to \lnot(A \to B))$ | : [T9] |
| (g) | $\lnot B \to \lnot(A \to B)$ | : (e),(f),MP |
□
このようにして、論理の定理がいくらでも形式的に証明できますが、キリがないのでここでやめておきます。
3. トートロジーが形式的証明可能なことの証明
ここまでの議論では、論理演算子 $\lnot, \to$ や推論規則には何の意味もなく、形式的証明はただ記号列を規則に従って並べているだけでした。これから論理演算子に意味を持たせ、論理式の真偽を定義します。
【定義7】(論理式の真偽)議論の対象としている原始命題それぞれに真理値と呼ばれる $\{$ 真, 偽 $\}$ どちらかの値が割り当てられているとする。このとき、論理式 $A$ の真理値を次で帰納的に与える。
i) $A$ が原始命題 $P$ のとき:
・$A$ の真理値は $P$ の真理値と同じ
ii) $A$ が $\lnot B$ で $B$ が論理式のとき:
・$B$ の真理値が真ならば $A$ の真理値は偽
・$B$ の真理値が偽ならば $A$ の真理値は真
(これは論理演算子 $\lnot$ に否定の意味を持たせることである。)
iii) $A$ が $B \to C$ で $B, C$ が論理式のとき:
・$B$ の真理値が真かつ $C$ の真理値が偽ならば $A$ の真理値は偽
・それ以外の場合は $A$ の真理値は真
(これは論理演算子 $\to$ に「ならば」の意味を持たせることである。)
論理式 $A$ の真理値が真のとき「$A$ は真」、真理値が偽のとき「$A$ は偽」という。
i) $A$ が原始命題 $P$ のとき:
・$A$ の真理値は $P$ の真理値と同じ
ii) $A$ が $\lnot B$ で $B$ が論理式のとき:
・$B$ の真理値が真ならば $A$ の真理値は偽
・$B$ の真理値が偽ならば $A$ の真理値は真
(これは論理演算子 $\lnot$ に否定の意味を持たせることである。)
iii) $A$ が $B \to C$ で $B, C$ が論理式のとき:
・$B$ の真理値が真かつ $C$ の真理値が偽ならば $A$ の真理値は偽
・それ以外の場合は $A$ の真理値は真
(これは論理演算子 $\to$ に「ならば」の意味を持たせることである。)
論理式 $A$ の真理値が真のとき「$A$ は真」、真理値が偽のとき「$A$ は偽」という。
【定義8】(論理的帰結)$\Sigma$ に属する論理式が全て真ならば論理式 $A$ が必ず真になるとき、$A$ は $\Sigma$ の論理的帰結であるといい、
\begin{equation*}
\Sigma \models A
\end{equation*}
と書く。$\Sigma$ が空集合のときは
\begin{equation*}
\models A
\end{equation*}
と書き、$A$ はトートロジー(恒真式)であるという。
トートロジーを言い換えると、原始命題の真理値をどのように割り当てても真になる論理式ということです。定義から具体的に検証することによって、論理の公理 [A1] $\sim$ [A3] は全てトートロジーになることが分かります。
このように論理式に真偽の意味を持たせると、形式的証明が次の定理によって意味づけされます。
【定理9】(健全性定理)$\Sigma \vdash A$ ならば $\Sigma \models A$ である。すなわち、$\Sigma$ から $A$ が形式的に証明できれば、$A$ は $\Sigma$ の論理的帰結である。
(証明)
$\Sigma \vdash A$ かつ $\Sigma$ の要素が全て真とする。$\Sigma$ から $A$ への形式的証明を $B_1, B_2, \cdots, B_{n-1}, A$ とし、$i < n$ に対して定理が成り立つ、すなわち $\Sigma \models B_i \ (i < n)$ であると仮定すると、$B_i \ (i < n)$ は全て真である。
i) $A$ が $\Sigma$ の要素のとき:
明らかに $A$ は真である。
ii) $A$ が [A1] $\sim$ [A3] のいずれかのとき:
[A1] $\sim$ [A3] はどれもトートロジーだから、やはり $A$ は真 である。
iii) ある $B_i, B_j \ (i,j < n)$ に対して $B_j$ が $B_i \to A$ のとき:
$B_i$ が真、かつ $B_i \to A$ が真 であるから、【定義7】iii) より $A$ は真でなければならない。
以上より全ての場合で $A$ が真であるから、形式的証明の長さ $n$ に関する帰納法によって $\Sigma \models A$ が示された。
□
つまり「形式的に証明できれば論理的に正しい」と言って良いわけです。これによって、論理の定理は前提なしで形式的に証明できるので、全てトートロジーです。
逆に、トートロジーが全て形式的に証明できること、すなわち論理の定理であることの証明に進みます。準備として、論理式の真理値と形式的証明の関係がよくわかる次の補題を証明します。
【補題10】論理式 $A$ を構成する原始命題は $P_1, P_2, \cdots , P_n$ 以外にないとする。$0 \le m \le n$ として、
(a) $P_1, \cdots , P_m$ が真、$P_{m+1}, \cdots , P_n$ が偽のときに $A$ が真ならば、 \begin{equation} \tag{3} \{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash A \end{equation} (b) $P_1, \cdots , P_m$ が真、$P_{m+1}, \cdots , P_n$ が偽のときに $A$ が偽ならば、 \begin{equation} \tag{4} \{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash \lnot A \end{equation}
(a) $P_1, \cdots , P_m$ が真、$P_{m+1}, \cdots , P_n$ が偽のときに $A$ が真ならば、 \begin{equation} \tag{3} \{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash A \end{equation} (b) $P_1, \cdots , P_m$ が真、$P_{m+1}, \cdots , P_n$ が偽のときに $A$ が偽ならば、 \begin{equation} \tag{4} \{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash \lnot A \end{equation}
(証明)
論理式 $A$ の構成に関する帰納法を用いる。
i) $A$ が原始命題 $P$ のとき:
(a) $P$ が真のとき $A$ は真である。このとき $\{ P \} \vdash P$ は自明だから $\{ P \} \vdash A$ となり、$(3)$が成立する。
(b) $P$ が偽のとき $A$ は偽である。このとき $\{ \lnot P \} \vdash \lnot P$ は自明だから $\{ \lnot P \} \vdash \lnot A$ となり、$(4)$が成立する。
ii) $A$ が $\lnot B$ で、$B$ について補題が成立するとき:
(a) $P_1, \cdots , P_m$ が真、$P_{m+1}, \cdots , P_n$ が偽のときに $A$ が真ならば、このとき $B$ は偽であるから、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash \lnot B
\end{equation*}
である。$\lnot B$ は $A$ だから$(3)$が成立する。
(b) $P_1, \cdots , P_m$ が真、$P_{m+1}, \cdots , P_n$ が偽のときに $A$ が偽ならば、このとき $B$ は真であるから、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash B
\end{equation*}
であり、さらに [T4] より $\vdash B \to \lnot \lnot B$ だから、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash \lnot \lnot B
\end{equation*}
である。$\lnot B$ は $A$ だから$(4)$が成立する。
iii) $A$ が $B \to C$ で、$B$ と $C$ について補題が成立するとき:
(a) $P_1, \cdots , P_m$ が真、$P_{m+1}, \cdots , P_n$ が偽のときに $A$ が真ならば、このとき $B$ が偽であるか、または $C$ が真である。
$B$ が偽の場合は、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash \lnot B
\end{equation*}
であり、さらに [T2] より $\vdash \lnot B \to (B \to C)$ だから、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash B \to C
\end{equation*}
である。$B \to C$ は $A$ だから$(3)$が成立する。
$C$ が真の場合は、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash C
\end{equation*}
であり、さらに [A1] より $\vdash C \to (B \to C)$ だから、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash B \to C
\end{equation*}
である。$B \to C$ は $A$ だから$(3)$が成立する。
(b) $P_1, \cdots , P_m$ が真、$P_{m+1}, \cdots , P_n$ が偽のときに $A$ が偽ならば、このとき $B$ が真かつ $C$ が偽であるから、
\begin{eqnarray*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} &\vdash& B \\
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} &\vdash& \lnot C
\end{eqnarray*}
であり、さらに [T10] より $\vdash B \to (\lnot C \to \lnot (B \to C))$ だから、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash \lnot (B \to C)
\end{equation*}
である。$B \to C$ は $A$ だから$(4)$が成立する。
以上より、全ての論理式 $A$ に対して補題が証明できた。
□
この補題を使って、本記事の目的である次の定理を証明します。
【定理11】$\models A$ ならば $\vdash A$ である。すなわちトートロジーは全て論理の定理である。
(証明)
$\models A$ とする。$A$ を構成する原始命題を全て取り出し $P_1, P_2, \cdots , P_n$ とすると、これらの真理値がどのように割り当てられても $A$ は真である。特に $P_n$ に注目すると、【補題10】より、
\begin{eqnarray*}
\{ P_1, \cdots , P_{n-1}, P_n \} &\vdash& A \\
\{ P_1, \cdots , P_{n-1}, \lnot P_n \} &\vdash& A
\end{eqnarray*}
である。これから演繹定理より、
\begin{eqnarray*}
\{ P_1, \cdots , P_{n-1} \} &\vdash& P_n \to A \\
\{ P_1, \cdots , P_{n-1} \} &\vdash& \lnot P_n \to A
\end{eqnarray*}
となる。一方 [T8] より、
\begin{equation*}
\vdash (P_n \to A) \to ((\lnot P_n \to A) \to A)
\end{equation*}
であるから、
\begin{equation*}
\{ P_1, \cdots , P_{n-2}, P_{n-1} \} \vdash A
\end{equation*}
が得られる。同様に、
\begin{eqnarray*}
\{ P_1, \cdots , P_{n-2}, \lnot P_{n-1}, P_n \} &\vdash& A \\
\{ P_1, \cdots , P_{n-2}, \lnot P_{n-1}, \lnot P_n \} &\vdash& A
\end{eqnarray*}
から
\begin{equation*}
\{ P_1, \cdots , P_{n-2}, \lnot P_{n-1} \} \vdash A
\end{equation*}
が得られる。従って、
\begin{eqnarray*}
\{ P_1, \cdots , P_{n-2}, P_{n-1} \} \vdash A \\
\{ P_1, \cdots , P_{n-2}, \lnot P_{n-1} \} \vdash A
\end{eqnarray*}
である。以下この操作を次々繰り返すと、最終的に
\begin{equation*}
\vdash A
\end{equation*}
が得られる。
□
たった3種類の公理系と1つの推論規則から全てのトートロジーが形式的に証明できることが、これで確認できました。
Wordle の成績の統計を取ってみた [日常生活]
去年から Wordle をほぼ毎日遊んでいます。
Wordle については有名なゲームなので、説明は省略しますが、毎日の通勤電車内での暇つぶしなどにちょうどいいです。
記録が200回分以上たまったので、ちょっと統計を取ってみました。
自分は英語を日常でも仕事でも使わないのであまり良い成績ではないですが、そのつもりで御覧ください。
まずは、「何回目で当てたか」に応じて、次のように「スコア」を決めます。
1回目で当てた → スコア 6
2回目で当てた → スコア 5
3回目で当てた → スコア 4
4回目で当てた → スコア 3
5回目で当てた → スコア 2
6回目で当てた → スコア 1
当たらなかった → スコア 0
このスコアを月別に度数分布表にしたのが次の表です。
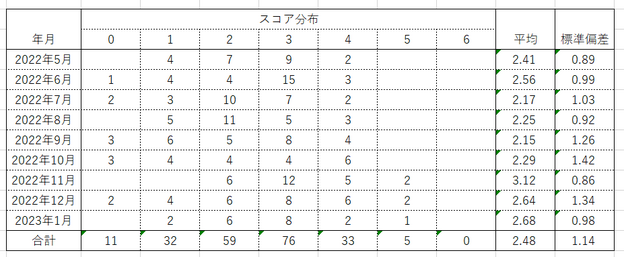
残念ながらスコア6、つまり1回目でズバリ当てたことはまだありませんが、スコア5(2回目で当てた)ことはこれまで5回あります(かなり嬉しい)。最頻値はスコア3(4回目で当てた)であることがわかります。
月ごとの平均値を見ると、11月は特に好成績ですが他の月はだいたい同じくらいです。そこでもっと傾向を見るために、箱ひげ図にしてみたのが次の図です。
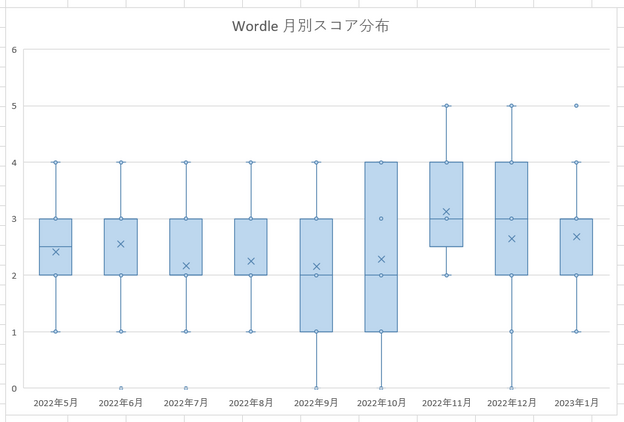
これを見ると、全体的に後の方になるほど、ちょっとカンが良くなっているようにも見えます。
ところで、このゲームは英単語の知識が必要とはいえ、初回に何文字ヒットするかは完全に当てもんの世界です。そして経験上、初回に緑でヒット(文字も位置も正解)する文字数が多いと正解にたどり着きやすいですが、黄でヒット(文字は正解だが位置は間違い)する文字数が多少あっても混乱するだけでなかなか正解しにくいことが多いです。典型例を出してみます。
[初回緑が2で、3回目で当てた例](2022/11/26の出題)

初回に2文字が位置まで特定できたので、後は順調に想像できた例です。
[初回黄が2で、6回目で当てた例](2022/12/6 の出題)
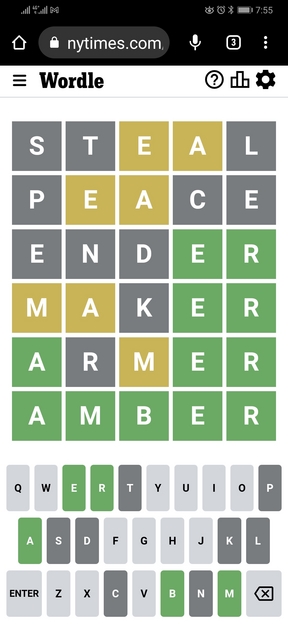
2文字はわかったものの位置がわからないので、なかなか正解が想像できず、結局6回目でようやく当てた例です。
このように感覚的には「緑は助けになるが黄はそれほど助けにならない」ことがわかるのですが、これを相関係数で確かめてみました。
初回に緑が出た数と、スコアとの相関は次になります。
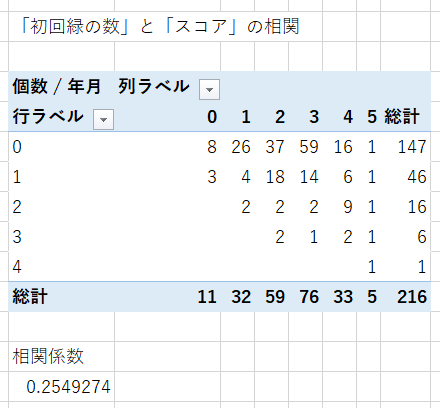
相関係数が 0.25 なので、「弱い正の相関あり」といえますね。
同様に初回に緑または黄が出た数と、スコアとの相関は次になります。
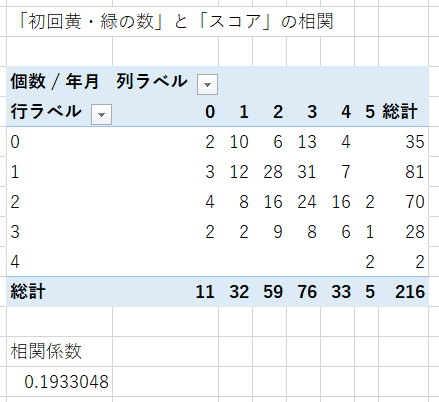
こちらは相関係数が 0.19 なので、ちょっと微妙ですが「ほとんど相関がない」といえます。
以上、暇に任せて分析してみました。
Wordle については有名なゲームなので、説明は省略しますが、毎日の通勤電車内での暇つぶしなどにちょうどいいです。
記録が200回分以上たまったので、ちょっと統計を取ってみました。
自分は英語を日常でも仕事でも使わないのであまり良い成績ではないですが、そのつもりで御覧ください。
まずは、「何回目で当てたか」に応じて、次のように「スコア」を決めます。
1回目で当てた → スコア 6
2回目で当てた → スコア 5
3回目で当てた → スコア 4
4回目で当てた → スコア 3
5回目で当てた → スコア 2
6回目で当てた → スコア 1
当たらなかった → スコア 0
このスコアを月別に度数分布表にしたのが次の表です。

残念ながらスコア6、つまり1回目でズバリ当てたことはまだありませんが、スコア5(2回目で当てた)ことはこれまで5回あります(かなり嬉しい)。最頻値はスコア3(4回目で当てた)であることがわかります。
月ごとの平均値を見ると、11月は特に好成績ですが他の月はだいたい同じくらいです。そこでもっと傾向を見るために、箱ひげ図にしてみたのが次の図です。

これを見ると、全体的に後の方になるほど、ちょっとカンが良くなっているようにも見えます。
ところで、このゲームは英単語の知識が必要とはいえ、初回に何文字ヒットするかは完全に当てもんの世界です。そして経験上、初回に緑でヒット(文字も位置も正解)する文字数が多いと正解にたどり着きやすいですが、黄でヒット(文字は正解だが位置は間違い)する文字数が多少あっても混乱するだけでなかなか正解しにくいことが多いです。典型例を出してみます。
[初回緑が2で、3回目で当てた例](2022/11/26の出題)

初回に2文字が位置まで特定できたので、後は順調に想像できた例です。
[初回黄が2で、6回目で当てた例](2022/12/6 の出題)

2文字はわかったものの位置がわからないので、なかなか正解が想像できず、結局6回目でようやく当てた例です。
このように感覚的には「緑は助けになるが黄はそれほど助けにならない」ことがわかるのですが、これを相関係数で確かめてみました。
初回に緑が出た数と、スコアとの相関は次になります。

相関係数が 0.25 なので、「弱い正の相関あり」といえますね。
同様に初回に緑または黄が出た数と、スコアとの相関は次になります。

こちらは相関係数が 0.19 なので、ちょっと微妙ですが「ほとんど相関がない」といえます。
以上、暇に任せて分析してみました。
冬の東吉野村を奈良交通とコミュニティバスで通り抜ける [バス]
激動の2022年の最後の乗りバス記事です。
年末の仕事納めの翌日が平日だったので、平日にしか走らない路線に乗りたくなり、奈良県の東吉野村に行ってきました。
ルートはこちら。
(東吉野村役場付近で1ヶ所途切れているのは、単に記録を忘れていたからです。)
吉野郡東吉野村は、平日のみ奈良交通バスが榛原駅から東吉野村役場まで走っていますが、土休日は途中の菟田野止まりになるので、東吉野村コミュニティバスでしかアクセスできません(それも休日は予約制になります)。
さらに、東吉野村から同じ吉野郡の吉野町へは、平日はコミュニティバスが新子まで走りますが、それも土休日は走らないので、平日にしかバスで吉野町へ抜けることができません。
今回は平日の年末休みを利用して、榛原から東吉野村を通って吉野町の大和上市まで通り抜けてきました。
榛原駅で東吉野村役場行に乗ります。時刻表の土休日欄には「運行はありません」と虚しく書かれています。


木津川水系の芳野川沿いに、県道を旧菟田野町に向けて南下していきます。


国道166号に入り、菟田野の中心地を抜けると、雪の残る風景になってきました。

峠を越えて東吉野村に入ると、道の駅「ひよしのさとマルシェ」に着きます。バスはこの先役場まで行きますが、昼食をとるためにここで下車します。



吉野本葛入りの太素麺「たあめん」を食べました。ツルッとしたうどんのような食感です。


ここは東吉野村コミュニティバスの路線結節点になっていて、各方面へのバスが集まってきます。


役場行きのバスに乗りました。
今度は吉野川水系の鷲家川に沿って走り、10分ほどで着きます。
運転席との間には感染防止対策シートがあるので、前面展望は良くないですが、仕方ありません。



役場もマルシェと同様に、奈良交通とコミュニティバスの乗換地点になっています。


国道から離れているので周辺はとても静かで、落ち着いた佇まいの集落が広がっています。地区内には小さな商店や南都銀行はありますが、コンビニやスーパーはありません。



ここからは平日にしか走らない新子(あたらし)行に乗って、吉野町へ向かいます。
吉野川の支流高見川に沿って走り、こちらも10分ほどで着きます。




新子からは吉野町内になるので、吉野町のコミュニティバス路線がありますが、今年の4月からダイヤが変わって、国道169号線沿いの路線以外は午前中にしか走らなくなりました。そのかわり予約制の乗合デマンドバスが運行されるようになり、町民以外も500円で利用できます(町民は200円)。新子からそれを使うことも考えましたが、なんだか単なる安いタクシーみたいな気もするので、今回は新子から国道169号線まで歩くことにしました。

このあたりも風情のある集落です。南都銀行の支店がこんな所にもあるのは少々驚きました(後で調べたら支店ではなくATMだけでした)。


吉野川が国道を離れて蛇行する区間の川沿いを4kmほど歩きます。天気が良いのでそれほど寒くなく快適なウォーキングでした。




国道169号線の樫尾のバス停に着きました。ここでは大和上市駅と川上村とを結ぶ「やまぶきバス」、それとはるばる奈良県の南の端の下北山村とを結ぶ「ゆうゆうバス」(どちらもコミュニティバス)が利用できます。今回はやまぶきバスに乗ります。

標柱にはスマイルバスと書かれていますが、今年4月からスマイルバスは樫尾は通っていません。

ゆうゆうバスの長い長い時刻表。いつかこれにも乗って熊野までバス乗り継ぎで抜けてみたいものです。

バスの時間まで間があるので、この付近の唯一の飲食店である焼肉屋で焼肉丼を食べて時間を潰しました。冬の乗りバスは待ち時間にどこで暖を取って過ごすかの計画も必要です。

やまぶきバスに乗って大和上市駅へ向かう頃にはすっかり暗くなりました。
近鉄の吉野川鉄橋が見えると、大和上市駅です。




この駅はかつては吉野郡東部地域の奈良交通バスの拠点だったのですが、いまや奈良交通の路線はほとんどなく、コミュニティバスばかりになりました。今年4月からは大台ヶ原行の路線も通らなくなってしまい(八木駅、橿原神宮前駅発着に変更)、寂しい限りです。


2両編成の近鉄特急で帰ります。

今回訪れた東吉野村も吉野町も、かつては奈良交通の路線がくまなく走っていた地域でしたが、コミュニティバス化は時代の流れで仕方がありません。運賃が安くなったメリットはありますが、自治体の方針によって、土休日の運行がなくなったりデマンドバス(タクシー)化などされたり、部外者が公共交通で訪問するには難しくなった面もあります。これからも各地をコミュニティバスを利用して訪れる場合は、事前によく調べた上で、できるだけ平日に休みを取って訪れたいと思います。
「路線バス歩き」のすすめ(目次)へ
年末の仕事納めの翌日が平日だったので、平日にしか走らない路線に乗りたくなり、奈良県の東吉野村に行ってきました。
ルートはこちら。
(東吉野村役場付近で1ヶ所途切れているのは、単に記録を忘れていたからです。)
吉野郡東吉野村は、平日のみ奈良交通バスが榛原駅から東吉野村役場まで走っていますが、土休日は途中の菟田野止まりになるので、東吉野村コミュニティバスでしかアクセスできません(それも休日は予約制になります)。
さらに、東吉野村から同じ吉野郡の吉野町へは、平日はコミュニティバスが新子まで走りますが、それも土休日は走らないので、平日にしかバスで吉野町へ抜けることができません。
今回は平日の年末休みを利用して、榛原から東吉野村を通って吉野町の大和上市まで通り抜けてきました。
榛原駅で東吉野村役場行に乗ります。時刻表の土休日欄には「運行はありません」と虚しく書かれています。


木津川水系の芳野川沿いに、県道を旧菟田野町に向けて南下していきます。


国道166号に入り、菟田野の中心地を抜けると、雪の残る風景になってきました。

峠を越えて東吉野村に入ると、道の駅「ひよしのさとマルシェ」に着きます。バスはこの先役場まで行きますが、昼食をとるためにここで下車します。



吉野本葛入りの太素麺「たあめん」を食べました。ツルッとしたうどんのような食感です。


ここは東吉野村コミュニティバスの路線結節点になっていて、各方面へのバスが集まってきます。


役場行きのバスに乗りました。
今度は吉野川水系の鷲家川に沿って走り、10分ほどで着きます。
運転席との間には感染防止対策シートがあるので、前面展望は良くないですが、仕方ありません。



役場もマルシェと同様に、奈良交通とコミュニティバスの乗換地点になっています。


国道から離れているので周辺はとても静かで、落ち着いた佇まいの集落が広がっています。地区内には小さな商店や南都銀行はありますが、コンビニやスーパーはありません。



ここからは平日にしか走らない新子(あたらし)行に乗って、吉野町へ向かいます。
吉野川の支流高見川に沿って走り、こちらも10分ほどで着きます。




新子からは吉野町内になるので、吉野町のコミュニティバス路線がありますが、今年の4月からダイヤが変わって、国道169号線沿いの路線以外は午前中にしか走らなくなりました。そのかわり予約制の乗合デマンドバスが運行されるようになり、町民以外も500円で利用できます(町民は200円)。新子からそれを使うことも考えましたが、なんだか単なる安いタクシーみたいな気もするので、今回は新子から国道169号線まで歩くことにしました。

このあたりも風情のある集落です。南都銀行の支店がこんな所にもあるのは少々驚きました(後で調べたら支店ではなくATMだけでした)。


吉野川が国道を離れて蛇行する区間の川沿いを4kmほど歩きます。天気が良いのでそれほど寒くなく快適なウォーキングでした。




国道169号線の樫尾のバス停に着きました。ここでは大和上市駅と川上村とを結ぶ「やまぶきバス」、それとはるばる奈良県の南の端の下北山村とを結ぶ「ゆうゆうバス」(どちらもコミュニティバス)が利用できます。今回はやまぶきバスに乗ります。

標柱にはスマイルバスと書かれていますが、今年4月からスマイルバスは樫尾は通っていません。

ゆうゆうバスの長い長い時刻表。いつかこれにも乗って熊野までバス乗り継ぎで抜けてみたいものです。

バスの時間まで間があるので、この付近の唯一の飲食店である焼肉屋で焼肉丼を食べて時間を潰しました。冬の乗りバスは待ち時間にどこで暖を取って過ごすかの計画も必要です。

やまぶきバスに乗って大和上市駅へ向かう頃にはすっかり暗くなりました。
近鉄の吉野川鉄橋が見えると、大和上市駅です。




この駅はかつては吉野郡東部地域の奈良交通バスの拠点だったのですが、いまや奈良交通の路線はほとんどなく、コミュニティバスばかりになりました。今年4月からは大台ヶ原行の路線も通らなくなってしまい(八木駅、橿原神宮前駅発着に変更)、寂しい限りです。


2両編成の近鉄特急で帰ります。

今回訪れた東吉野村も吉野町も、かつては奈良交通の路線がくまなく走っていた地域でしたが、コミュニティバス化は時代の流れで仕方がありません。運賃が安くなったメリットはありますが、自治体の方針によって、土休日の運行がなくなったりデマンドバス(タクシー)化などされたり、部外者が公共交通で訪問するには難しくなった面もあります。これからも各地をコミュニティバスを利用して訪れる場合は、事前によく調べた上で、できるだけ平日に休みを取って訪れたいと思います。
「路線バス歩き」のすすめ(目次)へ
シュトルツ・チェザロの定理の超準解析による証明 [数学]
久々に超準解析で証明問題をやってみました。
お題として「シュトルツ・チェザロの定理」です。
なんか見たことあるような雰囲気の定理ですが、これはあれです。「差分の比が収束すれば元の比も同じ値に収束する」という主張なので、差分を微分に変えたら有名なロピタルの定理になりますね。
また、$b_n = n, a_0 = 0$ としたら、これも有名な「実数列が収束すればそのチェザロ平均も同じ値に収束する」という定理にもなります。
では、証明していきましょう。以前の記事「チェザロ平均の収束の超準解析での証明例」のやり方に倣って進めます。
(証明)
実数列 $\{ a_n \}, \{ b_n \}$ を、超自然数を番号とする超実数列に拡大しておく。
任意の $m,n \in {}^*\mathbb{N}, m < n$ について、次が成り立つ。
\begin{eqnarray*}
a_n - a_m &=& \sum_{k=m}^{n-1}( a_{k+1} - a_k ) \\
&=& \sum_{k=m}^{n-1}( b_{k+1} - b_k ) \frac{ a_{k+1} - a_k }{ b_{k+1} - b_k }
\end{eqnarray*}
この全体を $b_n$ で割って両辺から $c$ を引くと、次の変形ができる。
\begin{eqnarray*}
\frac{ a_n }{ b_n } - c &=& \frac{ a_m }{ b_n } + \frac{1}{ b_n } \sum_{k=m}^{n-1}( b_{k+1} - b_k ) \frac{ a_{k+1} - a_k }{ b_{k+1} - b_k } - c \\
&=& \frac{ a_m }{ b_n } + \frac{1}{ b_n } \sum_{k=m}^{n-1}( b_{k+1} - b_k )( \frac{ a_{k+1} - a_k }{ b_{k+1} - b_k } - c ) + \frac{1}{ b_n } \sum_{k=m}^{n-1}( b_{k+1} - b_k ) c - c \\
&=& \frac{ a_m }{ b_n } + \frac{1}{ b_n } \sum_{k=m}^{n-1}( b_{k+1} - b_k )( \frac{ a_{k+1} - a_k }{ b_{k+1} - b_k } - c ) + \frac{1}{ b_n }( b_n - b_m ) c - c \\
&=& \frac{ a_m - b_m c }{ b_n } + \frac{1}{ b_n } \sum_{k=m}^{n-1}( b_{k+1} - b_k )( \frac{ a_{k+1} - a_k }{ b_{k+1} - b_k } - c )
\end{eqnarray*}
ここで、無限大超自然数 $n$ を任意にとる。$\displaystyle \lim_{n \to \infty} b_n = +\infty$ だから、この $n$ に対する $b_n$ は正の無限大超実数であり、従って $\sqrt{ b_n }$ も正の無限大超実数である。任意の自然数 $m$ に対して $a_m - b_m c$ は実数だから $\left| a_m - b_m c \right| < \sqrt{ b_n }$ であり、従って $m$ を十分小さな無限大超自然数にとると $\left| a_m - b_m c \right| < \sqrt{ b_n }$ とできる。この $m,n$ に対して、
\[ \mu = \max_{m \le k \le n-1} \left| \frac{ a_{k+1} - a_k }{ b_{k+1} - b_k } - c \right| \]
が存在し、
\[ \lim_{n \to \infty} \frac{a_{n+1} - a_n}{b_{n+1} - b_n} = c \]
より $\mu \approx 0$(無限小超実数)である。これらと $\{ b_n \}$ が狭義単調増加であることより、
\begin{eqnarray*}
\left| \frac{ a_n }{ b_n } - c \right| &\le& \frac{ \left| a_m - b_m c \right| }{ b_n } + \frac{1}{ b_n } \sum_{k=m}^{n-1}( b_{k+1} - b_k ) \left| \frac{ a_{k+1} - a_k }{ b_{k+1} - b_k } - c \right| \\
&<& \frac{\sqrt{ b_n }}{ b_n } + \frac{1}{ b_n } \sum_{k=m}^{n-1}( b_{k+1} - b_k ) \mu \\
&=& \frac{1}{\sqrt{ b_n }} + \frac{1}{ b_n } ( b_n - b_m ) \mu \\
&<& \frac{1}{\sqrt{ b_n }} + \mu \\
&\approx& 0
\end{eqnarray*}
従って、任意の無限大超自然数 $n$ に対して $\displaystyle \frac{a_n}{b_n} \approx c$ が成り立つから、$\displaystyle \lim_{n \to \infty} \frac{a_n}{b_n} = c$ である。□
どうでしょうか。普通の証明に比べて簡単になっているわけでもなさそうですが、やはり無限大や無限小を数として式変形して証明できるところは面白いかもしれません。
念のため、上の証明中に使った超準解析の基本的な補題を証明しておきましょう。
(証明)
$\{ a_n \}$ を超自然数を番号とする超実数列に拡大しておく。$K$ を任意の正の実数とし、$A_K = \{ \, k \in \mathbb{N} \, \mid \, \left| a_k \right| \ge K \, \}$ とおくと、自然数の性質より $A_K$ は空でなければ最小元をもつ。すなわち、
\[ \forall K \in \mathbb{R} \, ( K > 0 \land A_K \neq \emptyset \to \exists m \in \mathbb{N} \, ( m = \min A_K ) ) \]
移行原理より、
\[ \forall K \in {}^*\mathbb{R} \, ( K > 0 \land {}^*A_K \neq \emptyset \to \exists m \in {}^*\mathbb{N} \, ( m = \min {}^*A_K ) ) \]
ここで ${}^*A_K = \{ \, k \in {}^*\mathbb{N} \, \mid \, \left| a_k \right| \ge K \, \}$ であるから、これを $B_K$ とおく。
そこで、正の超実数 $M$ が任意の自然数 $k$ に対して $\left| a_k \right| < M$ であるとする。$B_M = \emptyset$ ならば、任意の無限大超自然数 $n$ に対して明らかに$(1)$は成立する。$B_M \neq \emptyset$ ならば、$m = \min B_M$ となる超自然数 $m$ が存在し、任意の自然数 $k$ に対して $k \notin B_M$ だから $m$ は無限大超自然数である。$n = m - 1$ とすると $n$ も無限大超自然数で、この $n$ に対し$(1)$が成立する。□
お題として「シュトルツ・チェザロの定理」です。
【定理】実数列 $\{ a_n \}, \{ b_n \}$ について、$\{ b_n \}$ は狭義単調増加で非有界、かつ極限
\[ \lim_{n \to \infty} \frac{a_{n+1} - a_n}{b_{n+1} - b_n} = c \]
が存在すれば、
\[ \lim_{n \to \infty} \frac{a_n}{b_n} = c \]
である。
なんか見たことあるような雰囲気の定理ですが、これはあれです。「差分の比が収束すれば元の比も同じ値に収束する」という主張なので、差分を微分に変えたら有名なロピタルの定理になりますね。
また、$b_n = n, a_0 = 0$ としたら、これも有名な「実数列が収束すればそのチェザロ平均も同じ値に収束する」という定理にもなります。
では、証明していきましょう。以前の記事「チェザロ平均の収束の超準解析での証明例」のやり方に倣って進めます。
(証明)
実数列 $\{ a_n \}, \{ b_n \}$ を、超自然数を番号とする超実数列に拡大しておく。
任意の $m,n \in {}^*\mathbb{N}, m < n$ について、次が成り立つ。
\begin{eqnarray*}
a_n - a_m &=& \sum_{k=m}^{n-1}( a_{k+1} - a_k ) \\
&=& \sum_{k=m}^{n-1}( b_{k+1} - b_k ) \frac{ a_{k+1} - a_k }{ b_{k+1} - b_k }
\end{eqnarray*}
この全体を $b_n$ で割って両辺から $c$ を引くと、次の変形ができる。
\begin{eqnarray*}
\frac{ a_n }{ b_n } - c &=& \frac{ a_m }{ b_n } + \frac{1}{ b_n } \sum_{k=m}^{n-1}( b_{k+1} - b_k ) \frac{ a_{k+1} - a_k }{ b_{k+1} - b_k } - c \\
&=& \frac{ a_m }{ b_n } + \frac{1}{ b_n } \sum_{k=m}^{n-1}( b_{k+1} - b_k )( \frac{ a_{k+1} - a_k }{ b_{k+1} - b_k } - c ) + \frac{1}{ b_n } \sum_{k=m}^{n-1}( b_{k+1} - b_k ) c - c \\
&=& \frac{ a_m }{ b_n } + \frac{1}{ b_n } \sum_{k=m}^{n-1}( b_{k+1} - b_k )( \frac{ a_{k+1} - a_k }{ b_{k+1} - b_k } - c ) + \frac{1}{ b_n }( b_n - b_m ) c - c \\
&=& \frac{ a_m - b_m c }{ b_n } + \frac{1}{ b_n } \sum_{k=m}^{n-1}( b_{k+1} - b_k )( \frac{ a_{k+1} - a_k }{ b_{k+1} - b_k } - c )
\end{eqnarray*}
ここで、無限大超自然数 $n$ を任意にとる。$\displaystyle \lim_{n \to \infty} b_n = +\infty$ だから、この $n$ に対する $b_n$ は正の無限大超実数であり、従って $\sqrt{ b_n }$ も正の無限大超実数である。任意の自然数 $m$ に対して $a_m - b_m c$ は実数だから $\left| a_m - b_m c \right| < \sqrt{ b_n }$ であり、従って $m$ を十分小さな無限大超自然数にとると $\left| a_m - b_m c \right| < \sqrt{ b_n }$ とできる。この $m,n$ に対して、
\[ \mu = \max_{m \le k \le n-1} \left| \frac{ a_{k+1} - a_k }{ b_{k+1} - b_k } - c \right| \]
が存在し、
\[ \lim_{n \to \infty} \frac{a_{n+1} - a_n}{b_{n+1} - b_n} = c \]
より $\mu \approx 0$(無限小超実数)である。これらと $\{ b_n \}$ が狭義単調増加であることより、
\begin{eqnarray*}
\left| \frac{ a_n }{ b_n } - c \right| &\le& \frac{ \left| a_m - b_m c \right| }{ b_n } + \frac{1}{ b_n } \sum_{k=m}^{n-1}( b_{k+1} - b_k ) \left| \frac{ a_{k+1} - a_k }{ b_{k+1} - b_k } - c \right| \\
&<& \frac{\sqrt{ b_n }}{ b_n } + \frac{1}{ b_n } \sum_{k=m}^{n-1}( b_{k+1} - b_k ) \mu \\
&=& \frac{1}{\sqrt{ b_n }} + \frac{1}{ b_n } ( b_n - b_m ) \mu \\
&<& \frac{1}{\sqrt{ b_n }} + \mu \\
&\approx& 0
\end{eqnarray*}
従って、任意の無限大超自然数 $n$ に対して $\displaystyle \frac{a_n}{b_n} \approx c$ が成り立つから、$\displaystyle \lim_{n \to \infty} \frac{a_n}{b_n} = c$ である。□
どうでしょうか。普通の証明に比べて簡単になっているわけでもなさそうですが、やはり無限大や無限小を数として式変形して証明できるところは面白いかもしれません。
念のため、上の証明中に使った超準解析の基本的な補題を証明しておきましょう。
【補題】実数列 $\{ a_n \}$ と正の超実数 $M$ について、任意の自然数 $k$ に対して $\left| a_k \right| < M$ ならば、ある無限大超自然数 $n$ が存在して、$\{ a_n \}$ を拡大した超実数列において、
\[ \forall k \in {}^*\mathbb{N} \, ( k \le n \to \left| a_k \right| < M ) \tag{1} \]
とすることができる。
(証明)
$\{ a_n \}$ を超自然数を番号とする超実数列に拡大しておく。$K$ を任意の正の実数とし、$A_K = \{ \, k \in \mathbb{N} \, \mid \, \left| a_k \right| \ge K \, \}$ とおくと、自然数の性質より $A_K$ は空でなければ最小元をもつ。すなわち、
\[ \forall K \in \mathbb{R} \, ( K > 0 \land A_K \neq \emptyset \to \exists m \in \mathbb{N} \, ( m = \min A_K ) ) \]
移行原理より、
\[ \forall K \in {}^*\mathbb{R} \, ( K > 0 \land {}^*A_K \neq \emptyset \to \exists m \in {}^*\mathbb{N} \, ( m = \min {}^*A_K ) ) \]
ここで ${}^*A_K = \{ \, k \in {}^*\mathbb{N} \, \mid \, \left| a_k \right| \ge K \, \}$ であるから、これを $B_K$ とおく。
そこで、正の超実数 $M$ が任意の自然数 $k$ に対して $\left| a_k \right| < M$ であるとする。$B_M = \emptyset$ ならば、任意の無限大超自然数 $n$ に対して明らかに$(1)$は成立する。$B_M \neq \emptyset$ ならば、$m = \min B_M$ となる超自然数 $m$ が存在し、任意の自然数 $k$ に対して $k \notin B_M$ だから $m$ は無限大超自然数である。$n = m - 1$ とすると $n$ も無限大超自然数で、この $n$ に対し$(1)$が成立する。□
北摂から秋の丹波路へ路線バス乗り継ぎで向かう [バス]
天気もよく、少し暑いくらいの10月の休日に、久しぶりの乗りバスです。
今回は千里中央から園部まで山越えルートで。
大阪府内は阪急バス、京都府内は京阪京都交通で、府境を越えるほんの少しの区間だけ徒歩になります。
数十年前までは京都交通(倒産しました)のバス路線が亀岡から府境を越えて余野まで走っていたので、千里中央から亀岡までバス乗り継ぎで行けました。今回このルートを辿って千里中央から亀岡市内、さらに園部を目指します。
たくさんのバスがひしめくターミナル千里中央から、ほぼ1時間に1本の希望ヶ丘二丁目行に乗ります。

新御堂筋を北上します。建設中の北大阪急行線の延伸部分が見えます。



白島北から東に向きを変え、住宅地内の山麓道路を粟生団地まで走ります。

粟生団地で折り返し、少し山道を走ったと思ったら、トンネルを抜けて彩都のニュータウン内に入ります。希望ヶ丘路線がこのルートに変わったのは2016年のことで、それまではほとんどの便がクリーンセンターを経由するひたすら山道のルートでした。



モノレールの彩都西駅を経由し、彩都を抜けて馬場からは北に向きを変え、本格的にカーブだらけの山道になります。



泉原付近は美しい棚田が広がっています。


峠を越えて豊能町に入ると、まもなく山の中のニュータウン希望ヶ丘に着きます。余野まで行く便もありますが、今回乗った便は希望ヶ丘二丁目が終点です。


すぐに牧経由池田行きが来ました。余野〜牧の間約2.7kmもの重複区間を折り返して池田に向かう路線です。池田方面に向かう乗客が何人かいましたが、わざわざ牧へ行って折り返すのは苦々しく思っているでしょう。

豊能町の役場がある余野地区を通り抜けます。


田園地帯を少し走ると、折り返し地点の牧に着きます。



阪急バスはこの先には行かないので徒歩になりますが、すぐに府境を越え、ほんの500m歩いて右側に物産店が見えたら京阪京都交通の神地バス停に着きます。



今回は乗り継ぎも良く、程なく京都先端化学大学行きの「亀岡市ふるさとバス」が来ました。

循環路線なので向きが2通りありますが、今回は万願寺経由の少し遠回りする便です。交通量の少ない道をのんびりした集落を縫って走ります。



山間部を抜けると少し開けた扇状地を下っていきます。


終点の京都先端科学大学京都亀岡キャンパスは、この地域のバス拠点になっていて、亀岡駅からの路線と支線路線がここで乗り継ぎとなります。


ここからもう一つのバス乗り継ぎ拠点である運動公園ターミナルまでも路線があるのですが、かなりの待ち時間があったし2kmほどの距離なので、歩いて向かうことにします。


途中の穴太寺でついでに参拝します。



運動公園ターミナルからは、亀岡駅から来て篠山街道を経由する園部行きのバスに乗ります。亀岡・南丹地区ではそこそこ長い距離を走る路線です。


湯の花温泉までは国道372号線ですが、その先からはほとんど旧道の狭い道を走ります。





八田からは篠山街道を離れ、田園地帯をしばらく走って市街地に入ると、まもなく終点の園部駅に到着です。



園部駅前は西口が京阪京都交通とコミュニティバスの乗り場、東口が福知山方面へ向かう西日本JRバスの乗り場になっています。西口広場は比較的新しく整備され、住宅地にも近いですが、商店はコンビニがあるくらいで少々寂しい状況です。

秋の空気ののどかな田舎道を、バスに揺られたり少し歩いたりして、気持ちよく過ごせた休日でした。
「路線バス歩き」のすすめ(目次)へ
今回は千里中央から園部まで山越えルートで。
大阪府内は阪急バス、京都府内は京阪京都交通で、府境を越えるほんの少しの区間だけ徒歩になります。
数十年前までは京都交通(倒産しました)のバス路線が亀岡から府境を越えて余野まで走っていたので、千里中央から亀岡までバス乗り継ぎで行けました。今回このルートを辿って千里中央から亀岡市内、さらに園部を目指します。
たくさんのバスがひしめくターミナル千里中央から、ほぼ1時間に1本の希望ヶ丘二丁目行に乗ります。


新御堂筋を北上します。建設中の北大阪急行線の延伸部分が見えます。



白島北から東に向きを変え、住宅地内の山麓道路を粟生団地まで走ります。

粟生団地で折り返し、少し山道を走ったと思ったら、トンネルを抜けて彩都のニュータウン内に入ります。希望ヶ丘路線がこのルートに変わったのは2016年のことで、それまではほとんどの便がクリーンセンターを経由するひたすら山道のルートでした。



モノレールの彩都西駅を経由し、彩都を抜けて馬場からは北に向きを変え、本格的にカーブだらけの山道になります。



泉原付近は美しい棚田が広がっています。


峠を越えて豊能町に入ると、まもなく山の中のニュータウン希望ヶ丘に着きます。余野まで行く便もありますが、今回乗った便は希望ヶ丘二丁目が終点です。


すぐに牧経由池田行きが来ました。余野〜牧の間約2.7kmもの重複区間を折り返して池田に向かう路線です。池田方面に向かう乗客が何人かいましたが、わざわざ牧へ行って折り返すのは苦々しく思っているでしょう。

豊能町の役場がある余野地区を通り抜けます。


田園地帯を少し走ると、折り返し地点の牧に着きます。



阪急バスはこの先には行かないので徒歩になりますが、すぐに府境を越え、ほんの500m歩いて右側に物産店が見えたら京阪京都交通の神地バス停に着きます。



今回は乗り継ぎも良く、程なく京都先端化学大学行きの「亀岡市ふるさとバス」が来ました。

循環路線なので向きが2通りありますが、今回は万願寺経由の少し遠回りする便です。交通量の少ない道をのんびりした集落を縫って走ります。



山間部を抜けると少し開けた扇状地を下っていきます。


終点の京都先端科学大学京都亀岡キャンパスは、この地域のバス拠点になっていて、亀岡駅からの路線と支線路線がここで乗り継ぎとなります。


ここからもう一つのバス乗り継ぎ拠点である運動公園ターミナルまでも路線があるのですが、かなりの待ち時間があったし2kmほどの距離なので、歩いて向かうことにします。


途中の穴太寺でついでに参拝します。



運動公園ターミナルからは、亀岡駅から来て篠山街道を経由する園部行きのバスに乗ります。亀岡・南丹地区ではそこそこ長い距離を走る路線です。



湯の花温泉までは国道372号線ですが、その先からはほとんど旧道の狭い道を走ります。





八田からは篠山街道を離れ、田園地帯をしばらく走って市街地に入ると、まもなく終点の園部駅に到着です。



園部駅前は西口が京阪京都交通とコミュニティバスの乗り場、東口が福知山方面へ向かう西日本JRバスの乗り場になっています。西口広場は比較的新しく整備され、住宅地にも近いですが、商店はコンビニがあるくらいで少々寂しい状況です。

秋の空気ののどかな田舎道を、バスに揺られたり少し歩いたりして、気持ちよく過ごせた休日でした。
「路線バス歩き」のすすめ(目次)へ



