【自由研究】超実数と距離空間(概要) [数学]
8/4に大阪で数学趣味の有志による「関西日曜数学友の会」が開催され、そこで私がタイトルの内容で発表しました。
発表のスライドを解説とともにここで公開します。

前半で超実数と超準解析についてのサワリを紹介し、後半で私の自由研究となる距離空間への応用を説明します。

まずは超実数とは何か、という説明です。実数体ℝは正確には 〈ℝ,+,∙,<,0,1〉で、その超準モデルは〈*ℝ,*+,*∙,*<,*0,*1〉(普通は演算等の*は省略して〈*ℝ,+,∙,<,0,1〉とかく)ですから、②の性質によって*ℝは順序体であり、実閉体でもあります。ただしデデキント完備性やアルキメデス性は一階の性質ではないので*ℝでは成立しません。
レーヴェンハイム・スコーレムの定理は「無限の領域を持つモデルはいくらでも大きな濃度の領域を持つモデルに拡大可能」ということを主張しますから、これらの性質をもつ超実数体*ℝはZFC上で存在し、また超積という手法を用いて実際に構成できます。これは無限の領域を持つどんなモデルであっても同じです。

超実数体における基本的な概念です。ここでℝ+は正実数の全体を表します。
これらの存在証明は、まず④から始まります。aが有限超実数(無限大でない超実数)であれば、それとの大小関係によるℝのデデキント切断が存在し、その境界となる実数cが定まるので、c=st(a) となります。次に①と②は互いに逆数関係になるのでどちらか一方の存在を証明すればよく、aを実数ではない超実数とすると、これが無限大超実数であればそれでよし、そうでなければ a-st(a) が0でない無限小超実数となります。
無限小超実数の全体は加法群であり、従って③の ≈ は同値関係です。また無限小超実数と有限超実数との積は無限小超実数ですから、無限小超実数の全体は有限超実数全体のなす環におけるイデアルとなり、それによる剰余環はℝと同型になります。
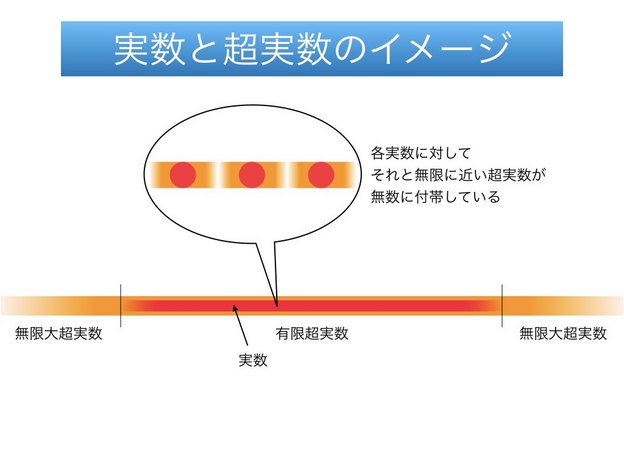
あまり正しい表現とは言えませんが、実数と超実数の関係を表すイメージ図です(実際には実数はこのような飛び飛びではありませんね)。実数のまわりに有限超実数がまとわりつき、その正負両方向の外側に無限大超実数が広がります。

超準解析のほんのサワリです。ℝの関数fを*ℝの関数*fに自然拡張するのは、これもモデル理論によって存在が示されますが、超積を用いても構成できます。これは何変数関数でも同様で、また関数だけではなく関係についても同様に自然拡張が存在します。部分集合は1変数の関係とみなせますのでこれも自然拡張できます。例えば自然数の全体ℕを超自然数の全体*ℕに拡張できます。
微分の表現を見るとわかるように、「無限小変化の比の標準部分」が微分係数です。dx,dyは何を表すのか理解しにくかったのですが、Δx,Δyの方は無限小超実数という「数」であり、四則演算が自由に行えるところが超準解析の醍醐味となります。例えばここから関数の積の導関数の公式が数式の四則演算処理でいとも簡単に導かれます。もう一つ例をあげると、ロピタルの定理の∞/∞バージョンの証明は通常のやり方では少々面倒臭いのですが、超実数を使うと無限大の範囲でコーシーの平均値の定理が成り立ちますので、もうちょっとスッキリした証明ができます。
ここまではネットでも調べることができる超実数と超準解析の紹介でした。ここからが私の自由研究になります。

一般の距離空間(ただし領域は無限集合とします)についても、超準モデルが考えられます。このとき距離関数dの自然拡張*dは移行原理によって*Xから*ℝへの2変数関数になります。距離関数の性質i)〜iii)は全て一階の性質ですから、*dも同じ性質をもちます。この*dによる「*距離」が無限小であることをもって「2点が無限に近い」という関係 ≈ が定義でき、明らかにこれは同値関係です。

距離空間における色々な概念が、超準モデルを用いた簡単な論理式と同値になるということを説明しています。これらの証明はℝにおける超準解析と類似の手法で行えます。①の開集合の場合を日本語でかくと「Aの点と無限に近い*Xの点は全て*Aの点である」となります。オレンジで書かれた定理は①と③の論理式を突き合わせるだけで簡単に導けますね。

同様に、コンパクト性とそれに関連する諸概念を超準モデルを用いた同値な論理式で表したものです(特にコンパクト性はいかにも強力な性質にみえます)。これらの証明は少々複雑ですが、難しいものではありません。オレンジ色で書かれた距離空間における有名な定理は、やはりこれらの論理式を突き合わせると簡単に導けます。具体的には、赤色から青色が従うことは明らかですから①→②、あとは赤色と青色の対応をみることで①→③と②∧③→①が簡単にわかります。

最後に、超準モデルを用いた距離空間の完備化です。コーシー列を用いた完備化と本質的に変わらないかもしれませんが、距離空間の「点」や「距離」と同じように扱えるため、よりわかりやすくなっているように思います。
発表内容は以上でした。距離空間への応用は面白いので、もう少し深く掘り下げていこうと思います。
発表のスライドを解説とともにここで公開します。

前半で超実数と超準解析についてのサワリを紹介し、後半で私の自由研究となる距離空間への応用を説明します。

まずは超実数とは何か、という説明です。実数体ℝは正確には 〈ℝ,+,∙,<,0,1〉で、その超準モデルは〈*ℝ,*+,*∙,*<,*0,*1〉(普通は演算等の*は省略して〈*ℝ,+,∙,<,0,1〉とかく)ですから、②の性質によって*ℝは順序体であり、実閉体でもあります。ただしデデキント完備性やアルキメデス性は一階の性質ではないので*ℝでは成立しません。
レーヴェンハイム・スコーレムの定理は「無限の領域を持つモデルはいくらでも大きな濃度の領域を持つモデルに拡大可能」ということを主張しますから、これらの性質をもつ超実数体*ℝはZFC上で存在し、また超積という手法を用いて実際に構成できます。これは無限の領域を持つどんなモデルであっても同じです。

超実数体における基本的な概念です。ここでℝ+は正実数の全体を表します。
これらの存在証明は、まず④から始まります。aが有限超実数(無限大でない超実数)であれば、それとの大小関係によるℝのデデキント切断が存在し、その境界となる実数cが定まるので、c=st(a) となります。次に①と②は互いに逆数関係になるのでどちらか一方の存在を証明すればよく、aを実数ではない超実数とすると、これが無限大超実数であればそれでよし、そうでなければ a-st(a) が0でない無限小超実数となります。
無限小超実数の全体は加法群であり、従って③の ≈ は同値関係です。また無限小超実数と有限超実数との積は無限小超実数ですから、無限小超実数の全体は有限超実数全体のなす環におけるイデアルとなり、それによる剰余環はℝと同型になります。

あまり正しい表現とは言えませんが、実数と超実数の関係を表すイメージ図です(実際には実数はこのような飛び飛びではありませんね)。実数のまわりに有限超実数がまとわりつき、その正負両方向の外側に無限大超実数が広がります。

超準解析のほんのサワリです。ℝの関数fを*ℝの関数*fに自然拡張するのは、これもモデル理論によって存在が示されますが、超積を用いても構成できます。これは何変数関数でも同様で、また関数だけではなく関係についても同様に自然拡張が存在します。部分集合は1変数の関係とみなせますのでこれも自然拡張できます。例えば自然数の全体ℕを超自然数の全体*ℕに拡張できます。
微分の表現を見るとわかるように、「無限小変化の比の標準部分」が微分係数です。dx,dyは何を表すのか理解しにくかったのですが、Δx,Δyの方は無限小超実数という「数」であり、四則演算が自由に行えるところが超準解析の醍醐味となります。例えばここから関数の積の導関数の公式が数式の四則演算処理でいとも簡単に導かれます。もう一つ例をあげると、ロピタルの定理の∞/∞バージョンの証明は通常のやり方では少々面倒臭いのですが、超実数を使うと無限大の範囲でコーシーの平均値の定理が成り立ちますので、もうちょっとスッキリした証明ができます。
ここまではネットでも調べることができる超実数と超準解析の紹介でした。ここからが私の自由研究になります。

一般の距離空間(ただし領域は無限集合とします)についても、超準モデルが考えられます。このとき距離関数dの自然拡張*dは移行原理によって*Xから*ℝへの2変数関数になります。距離関数の性質i)〜iii)は全て一階の性質ですから、*dも同じ性質をもちます。この*dによる「*距離」が無限小であることをもって「2点が無限に近い」という関係 ≈ が定義でき、明らかにこれは同値関係です。

距離空間における色々な概念が、超準モデルを用いた簡単な論理式と同値になるということを説明しています。これらの証明はℝにおける超準解析と類似の手法で行えます。①の開集合の場合を日本語でかくと「Aの点と無限に近い*Xの点は全て*Aの点である」となります。オレンジで書かれた定理は①と③の論理式を突き合わせるだけで簡単に導けますね。

同様に、コンパクト性とそれに関連する諸概念を超準モデルを用いた同値な論理式で表したものです(特にコンパクト性はいかにも強力な性質にみえます)。これらの証明は少々複雑ですが、難しいものではありません。オレンジ色で書かれた距離空間における有名な定理は、やはりこれらの論理式を突き合わせると簡単に導けます。具体的には、赤色から青色が従うことは明らかですから①→②、あとは赤色と青色の対応をみることで①→③と②∧③→①が簡単にわかります。

最後に、超準モデルを用いた距離空間の完備化です。コーシー列を用いた完備化と本質的に変わらないかもしれませんが、距離空間の「点」や「距離」と同じように扱えるため、よりわかりやすくなっているように思います。
発表内容は以上でした。距離空間への応用は面白いので、もう少し深く掘り下げていこうと思います。




コメント 0