わかってない奴がわかったつもりで書き留める超準解析(その18) [数学]
【超準解析について生半可な知識しかない僕が、わかったつもりの内容をちょっとずつ書き留めていきます。不正確な内容や誤りもあることをご承知ください。】
(18) アレクサンドロフの1点コンパクト化
前回の続きとして、コンパクトでない空間をコンパクト空間に拡張する1つの手法「アレクサンドロフの1点コンパクト化」を、超準モデルを使って構成する方法を紹介します。
1. 超準モデルから定まる位相
$X$ を位相が定まっていない無限集合とするとき、その超準モデルを使って、次のようにして $X$ に位相を定めることができます。
すべての $X$ の点 $x$ に対して $x \in \nu(x)$ をみたす ${}^*X$ の部分集合 $\nu(x) \in \mathscr{P}({}^*X)$ が(何でもよいので)定まっているとします。このとき、
\begin{equation*}
\mathcal{O} = \{ \, A \in \mathscr{P}(X) \, \mid \, \forall x \in A \, (\nu(x) \subseteq {}^*A) \, \}
\end{equation*}
と定めると、この $\mathcal{O}$ は次の開集合系の性質を全てみたします。
① $\emptyset \in \mathcal{O} \land X \in \mathcal{O}$
② $A \in \mathcal{O} \land B \in \mathcal{O} \to A \cap B \in \mathcal{O}$
③ $\forall i \in I \, (A_i \in \mathcal{O}) \to \bigcup_{i \in I} A_i \in \mathcal{O}$
①と②は明らかなので、和集合に関する性質③だけ示しておきます。$\forall i \in I \, (A_i \in \mathcal{O})$ が成り立つとし、$B = \bigcup_{i \in I} A_i$ とします。任意に $x \in B$ をとると、ある $i \in I$ に対して $x \in A_i$ だから $\nu(x) \subseteq {}^*A_i$ となります。$A_i \subseteq B$ だから移行原理より ${}^*A_i \subseteq {}^*B$ となり、従って $\nu(x) \subseteq {}^*B$ となるから $B \in \mathcal{O}$ です。これで $\mathcal{O}$ が開集合系の性質を全てみたすことが示されたので、$X$ に位相が定まります。
この位相に関して近傍系やモナドが定まりますが、$A$ が点 $x$ の近傍ならば簡単な考察により $\nu(x) \subseteq {}^*A$ がわかるので、$\nu(x) \subseteq \mathrm{monad}(x)$ となります。一般には必ずしもこれらは等しくなりません。
この方法を使って位相空間 $X$ を $X \subsetneq Y$ となる集合 $Y$ に拡張することを考えます。このため、一般に一方が他方の部分位相空間となるための超準モデルによる同値条件を考察します。
$X \subseteq Y$ の関係にある位相空間 $X, Y$ がそれぞれあるとします。$X$ と $Y$ の開集合系をそれぞれ $\mathcal{O}_X, \mathcal{O}_Y$ とし、また、$X$ における点 $x$ の近傍系とモナドをそれぞれ $\mathcal{N}_X(x), \mathrm{monad}_X(x)$ とかき、同様に $Y$ における点 $x$ の近傍系とモナドをそれぞれ $\mathcal{N}_Y(x), \mathrm{monad}_Y(x)$ とかくことにします。このとき、$X$ が $Y$ の部分位相空間であるとは、
\begin{equation} \tag{1}
\forall A \in \mathscr{P}(X) \, (A \in \mathcal{O}_X \leftrightarrow \exists B \in \mathcal{O}_Y \, (A = B \cap X))
\end{equation}
であることをいいます。
これを超準モデルでの同値条件で表したものが次の定理です。
(証明)$(1) \Leftrightarrow (2)$ を示せばよい。
$(1) \Rightarrow (2)$ : $(1)$ が成り立つとし、任意に $x \in X$ をとる。
任意に $B \in \mathcal{N}_Y(x)$ をとると、$x \in B' \subseteq B$ となる $B' \in \mathcal{O}_Y$ がとれ、$A' = B' \cap X$ とすると $(1)$ より $A' \in \mathcal{O}_X$ で、$x \in A'$ だから
\begin{equation*}
\mathrm{monad}_X(x) \subseteq {}^*A' \subseteq {}^*B' \subseteq {}^*B
\end{equation*}
である。$B \in \mathcal{N}_Y(x)$ は任意だから $\mathrm{monad}_X(x) \subseteq \mathrm{monad}_Y(x)$ であり、また $\mathrm{monad}_X(x) \subseteq {}^*X$ は明らかだから $\mathrm{monad}_X(x) \subseteq \mathrm{monad}_Y(x) \cap {}^*X$ が得られる。
逆に、任意に $A \in \mathcal{N}_X(x)$ をとると、$x \in A' \subseteq A$ となる $A' \in \mathcal{O}_X$ がとれ、$(1)$ よりある $B' \in \mathcal{O}_Y$ に対して $A' = B' \cap X$ となり、$x \in B'$ だから $\mathrm{monad}_Y(x) \subseteq {}^*B'$ より
\begin{equation*}
\mathrm{monad}_Y(x) \cap {}^*X \subseteq {}^*B' \cap {}^*X = {}^*A' \subseteq {}^*A
\end{equation*}
であり、$A \in \mathcal{N}_X(x)$ は任意だから $\mathrm{monad}_Y(x) \cap {}^*X \subseteq \mathrm{monad}_X(x)$ が得られる。
以上より $\mathrm{monad}_X(x) = \mathrm{monad}_Y(x) \cap {}^*X$ であり、$(2)$ が示された。
$(2) \Rightarrow (1)$ : $(2)$ が成り立つとし、任意に $A \in \mathscr{P}(X)$ をとる。
$A \in \mathcal{O}_X$ とする。$B' = A \cup (Y \setminus X)$ とおき、任意の $x \in A$ に対して $\mathrm{monad}_Y(x) \subseteq {}^*B'$ となることを示す。任意に $y \in \mathrm{monad}_Y(x)$ をとると、$y \in {}^*X$ ならば $(2)$ より
\begin{equation*}
y \in \mathrm{monad}_Y(x) \cap {}^*X = \mathrm{monad}_X(x) \subseteq {}^*A \subseteq {}^*B'
\end{equation*}
となるから $y \in {}^*B'$ である。$y \notin {}^*X$ ならば
\begin{equation*}
y \in {}^*Y \setminus {}^*X = {}^*(Y \setminus X) \subseteq {}^*B'
\end{equation*}
よりやはり $y \in {}^*B'$ である。これで $\mathrm{monad}_Y(x) \subseteq {}^*B'$ が示されたから $B' \in \mathcal{N}_Y(x)$ であり、$x \in B(x) \subseteq B'$ をみたす $B(x) \in \mathcal{O}_Y$ が存在する。$B = \bigcup_{x \in A}B(x)$ とおくと $B \in \mathcal{O}_Y$ かつ $B \subseteq B'$ で、明らかに $A \subseteq B \cap X$ であり、また $B \cap X \subseteq B' \cap X = A$ だから $A = B \cap X$ である。
逆に、ある $B \in \mathcal{O}_Y$ に対して $A = B \cap X$ ならば、任意の $x \in A$ に対して、$\mathrm{monad}_Y(x) \subseteq {}^*B$ と $(2)$ より
\begin{equation*}
\mathrm{monad}_X(x) = \mathrm{monad}_Y(x) \cap {}^*X \subseteq {}^*B \cap {}^*X = {}^*A
\end{equation*}
が得られるから、$A \in \mathcal{O}_X$ である。
以上より $A \in \mathcal{O}_X \leftrightarrow \exists B \in \mathcal{O}_Y \, (A = B \cap X)$ であり、$(1)$ が示された。□
さて、超準モデルを使って位相空間 $X$ を $X \subsetneq Y$ となる $Y$ に拡張する一つの方法を、次の補題によって示します。
(証明)
任意に $x \in X$ をとる。まず、$\mathrm{monad}_X(x) = \nu(x) \subseteq \mathrm{monad}_Y(x)$ である。逆の包含関係を示すため、任意に $A \in \mathcal{N}_X(x)$ をとると、$x \in B \subseteq A$ となる $B \in \mathcal{O}_X$ が存在し、$\forall y \in B \, (\nu(y) = \mathrm{monad}_X(y) \subseteq {}^*B)$ より $B \in \mathcal{O}_Y$ となるから $A \in \mathcal{N}_Y(x)$ であり、これより $\mathrm{monad}_Y(x) \subseteq {}^*A$ である。$A \in \mathcal{N}_X(x)$ は任意だから $\mathrm{monad}_Y(x) \subseteq \mathrm{monad}_X(x)$ が得られる。以上で $(3)$ が示された。□
この補題の方法は、本来は $(2)$ でよいのにそれより強い $(3)$ が得られることから、位相空間の拡張手段としてはかなり「雑」といえます。しかし次に示す目的のためには、この方法で十分です。
2. アレクサンドロフの1点コンパクト化
ここまでの考察を利用して、「アレクサンドロフの1点コンパクト化」を超準モデルを用いて構成します。
位相空間 $X$ に対し、$X$ に属さない1点 $\infty$ を $X$ に追加した空間 $Y = X \cup \{ \infty \}$ を考え、次によって $\nu(\infty)$ を定めます。
\begin{equation*}
\nu(\infty) = \{ \, y \in {}^*X \, \mid \, \forall x \in X \, (y \notin \mathrm{monad}_X(x)) \, \} \cup \{ \infty \}
\end{equation*}
つまり「 ${}^*X$ のすべての遠標準点と $\infty$ を集めた集合」を $\nu(\infty)$ と定めます。
これを用いて【補題2】の方法で $X$ を部分位相空間とする $Y$ の位相が定まります。$(3)$ が成立するので、以下 $\mathrm{monad}$ の添字は省略します。
このとき、まず $Y$ はコンパクトです。なぜなら任意に $y \in {}^*Y$ をとると、$y$ はある $x \in X$ に対して $y \in \mathrm{monad}(x)$ となるか、または $y \in \nu(\infty)$ となるかのどちらかで、後者ならば $y \in \nu(\infty) \subseteq \mathrm{monad}(\infty)$ なので、第17回【定理5】より $Y$ はコンパクトになります。
次に、$X$ がコンパクトでない場合、$X$ は $Y$ において稠密となります。なぜなら $X$ がコンパクトでなければ ${}^*X$ は遠標準点をもつから $\nu(\infty) \cap {}^*X \neq \emptyset$ であり、従って $\mathrm{monad}(\infty) \cap {}^*X \neq \emptyset$ より $\forall x \in Y \, ( \mathrm{monad}(x) \cap {}^*X \neq \emptyset )$ となるから、第17回【定理3】の ix) より $X$ は $Y$ において稠密です。
これらの条件をみたす $Y = X \cup \{ \infty \}$ を $X$ のアレクサンドロフの1点コンパクト化といいます。従って上の方法は、任意のコンパクトでない位相空間から1点コンパクト化を構成する(超準モデルを使った)一つの方法を示しています。
さらに次が成り立ちます。
(証明)
$\mathrm{monad}(\infty) \supseteq \nu(\infty)$ は既に証明済み。$\mathrm{monad}(\infty) \subseteq \nu(\infty)$ を示すため、ある $ y \in \mathrm{monad}(\infty) \setminus \nu(\infty)$ が存在すると仮定して矛盾を導く。$y \notin \nu(\infty)$ なので、$\nu(\infty)$ の定義より、ある $x \in X$ に対して $y \in \mathrm{monad}(x)$ である。$X$ は局所コンパクトだから $A \in \mathcal{N}_X(x)$ となるコンパクトな $A$ が存在して $y \in \mathrm{monad}(x) \subseteq {}^*A$ より $y \in {}^*A$ となる。$X$ はハウスドルフだから第17回【定理6】 ii) より $A$ は $X$ の閉集合で、従って $X \setminus A$ は $X$ の開集合である。そこで $B = (X \setminus A) \cup \{ \infty \}$ とすると $B = Y \setminus A$ で、任意の $z \in X \setminus A$ に対して $\nu(z) = \mathrm{monad}(z) \subseteq {}^*(X \setminus A) \subseteq {}^*B$ である。また $A$ がコンパクトだから第17回【定理5】より ${}^*A$ の点は全て ${}^*X$ の近標準点で、$\nu(\infty)$ は ${}^*X$ の遠標準点と $\infty$ の集合だから $\nu(\infty) \cap {}^*A = \emptyset$ であり、これより $\nu(\infty) \subseteq {}^*Y \setminus {}^*A = {}^*(Y \setminus A) = {}^*B$ となる。従って $B$ は $Y$ における開集合であるから $\infty$ の近傍であり、 $y \in \mathrm{monad}(\infty) \subseteq {}^*B = {}^*Y \setminus {}^*A$ となるから $y \in {}^*A$ と矛盾する。以上より $\mathrm{monad}(\infty) \subseteq \nu(\infty)$ が得られたから $\mathrm{monad}(\infty) = \nu(\infty)$ である。□
この補題を使って、次の有名な結果が示されます。
(証明)
$X$ がハウスドルフであることと第17回【定理4】 ii) より、任意の $x, y \in X$ に対して $x \neq y \to \mathrm{monad}(x) \cap \mathrm{monad}(y) = \emptyset$ である。さらに【補題3】より $\mathrm{monad}(x) \cap \mathrm{monad}(\infty) = \mathrm{monad}(x) \cap \nu(\infty) = \emptyset$ も明らかなので、任意の $x, y \in Y$ に対して $x \neq y \to \mathrm{monad}(x) \cap \mathrm{monad}(y) = \emptyset$ が成り立ち、従って再び第17回【定理4】 ii) より $Y$ もハウスドルフである。□
ついでに、この定理の逆も超準モデルを利用して示しておきましょう。そのために必要になるのが次の補題です。
(証明)
【定理1】より任意の $x \in X$ に対して
\begin{equation*}
\mathrm{monad}_X(x) = \mathrm{monad}_Y(x) \cap {}^*X
\end{equation*}
が成立する。$Y$ が $\mathrm{T}_1$ だから第17回【定理4】 i) より $\infty \notin \mathrm{monad}_Y(x)$ であり、かつ ${}^*Y = {}^*X \cup \{ \infty \}$ だから $\mathrm{monad}_Y(x) \subseteq {}^*X$ すなわち $\mathrm{monad}_Y(x) \cap {}^*X = \mathrm{monad}_Y(x)$ である。従って $(4)$ が成立する。□
この補題を使って、【定理4】の逆が次のように示されます。
(証明)
$Y$ はハウスドルフだから $\mathrm{T}_1$ であり、【補題5】より $(4)$ が成立する。従って $Y$ のハウスドルフ性と第17回【定理4】 ii) より $X$ もハウスドルフである。任意に $x \in X$ をとると、$Y$ がハウスドルフだから $Y$ における $x$ の開近傍 $A$ と $\infty$ の開近傍 $B$ で $A \cap B = \emptyset$ となるものがとれる。$C = Y \setminus B$ とすると、$C$ はコンパクト空間 $Y$ の閉集合だから、第17回【定理6】 i) より $Y$ においてコンパクトである。従って第17回【定理5】より、
\begin{equation*}
\forall y \in {}^*C \, \exists z \in C \, (y \in \mathrm{monad}_Y(z))
\end{equation*}
が成立するが、$\infty \notin C$ より $C \subseteq X$ であり、これと $(4)$ より
\begin{equation*}
\forall y \in {}^*C \, \exists z \in C \, (y \in \mathrm{monad}_X(z))
\end{equation*}
が成立し、第17回【定理5】より $C$ は $X$ においてもコンパクトである。$A \subseteq C$ だから $C$ は $x$ のコンパクトな近傍であり、$x \in X$ は任意だから $X$ は局所コンパクトである。□
以上でアレクサンドロフの1点コンパクト化に関する諸定理が、超準モデルを使って証明されました。通常の方法に比べて特に簡単になるとは言えませんが、ハウスドルフ性やコンパクト性とモナドとの関係を見通しよく利用することができて、面白い方法だと思います。
(続く)(前記事)(目次)
(18) アレクサンドロフの1点コンパクト化
前回の続きとして、コンパクトでない空間をコンパクト空間に拡張する1つの手法「アレクサンドロフの1点コンパクト化」を、超準モデルを使って構成する方法を紹介します。
1. 超準モデルから定まる位相
$X$ を位相が定まっていない無限集合とするとき、その超準モデルを使って、次のようにして $X$ に位相を定めることができます。
すべての $X$ の点 $x$ に対して $x \in \nu(x)$ をみたす ${}^*X$ の部分集合 $\nu(x) \in \mathscr{P}({}^*X)$ が(何でもよいので)定まっているとします。このとき、
\begin{equation*}
\mathcal{O} = \{ \, A \in \mathscr{P}(X) \, \mid \, \forall x \in A \, (\nu(x) \subseteq {}^*A) \, \}
\end{equation*}
と定めると、この $\mathcal{O}$ は次の開集合系の性質を全てみたします。
① $\emptyset \in \mathcal{O} \land X \in \mathcal{O}$
② $A \in \mathcal{O} \land B \in \mathcal{O} \to A \cap B \in \mathcal{O}$
③ $\forall i \in I \, (A_i \in \mathcal{O}) \to \bigcup_{i \in I} A_i \in \mathcal{O}$
①と②は明らかなので、和集合に関する性質③だけ示しておきます。$\forall i \in I \, (A_i \in \mathcal{O})$ が成り立つとし、$B = \bigcup_{i \in I} A_i$ とします。任意に $x \in B$ をとると、ある $i \in I$ に対して $x \in A_i$ だから $\nu(x) \subseteq {}^*A_i$ となります。$A_i \subseteq B$ だから移行原理より ${}^*A_i \subseteq {}^*B$ となり、従って $\nu(x) \subseteq {}^*B$ となるから $B \in \mathcal{O}$ です。これで $\mathcal{O}$ が開集合系の性質を全てみたすことが示されたので、$X$ に位相が定まります。
この位相に関して近傍系やモナドが定まりますが、$A$ が点 $x$ の近傍ならば簡単な考察により $\nu(x) \subseteq {}^*A$ がわかるので、$\nu(x) \subseteq \mathrm{monad}(x)$ となります。一般には必ずしもこれらは等しくなりません。
この方法を使って位相空間 $X$ を $X \subsetneq Y$ となる集合 $Y$ に拡張することを考えます。このため、一般に一方が他方の部分位相空間となるための超準モデルによる同値条件を考察します。
$X \subseteq Y$ の関係にある位相空間 $X, Y$ がそれぞれあるとします。$X$ と $Y$ の開集合系をそれぞれ $\mathcal{O}_X, \mathcal{O}_Y$ とし、また、$X$ における点 $x$ の近傍系とモナドをそれぞれ $\mathcal{N}_X(x), \mathrm{monad}_X(x)$ とかき、同様に $Y$ における点 $x$ の近傍系とモナドをそれぞれ $\mathcal{N}_Y(x), \mathrm{monad}_Y(x)$ とかくことにします。このとき、$X$ が $Y$ の部分位相空間であるとは、
\begin{equation} \tag{1}
\forall A \in \mathscr{P}(X) \, (A \in \mathcal{O}_X \leftrightarrow \exists B \in \mathcal{O}_Y \, (A = B \cap X))
\end{equation}
であることをいいます。
これを超準モデルでの同値条件で表したものが次の定理です。
【定理1】位相空間 $X,Y$ が $X \subseteq Y$ のとき、$X$ が $Y$ の部分位相空間となることは、
\begin{equation} \tag{2}
\forall x \in X \, (\mathrm{monad}_X(x) = \mathrm{monad}_Y(x) \cap {}^*X)
\end{equation}
が成り立つことと同値である。
(証明)$(1) \Leftrightarrow (2)$ を示せばよい。
$(1) \Rightarrow (2)$ : $(1)$ が成り立つとし、任意に $x \in X$ をとる。
任意に $B \in \mathcal{N}_Y(x)$ をとると、$x \in B' \subseteq B$ となる $B' \in \mathcal{O}_Y$ がとれ、$A' = B' \cap X$ とすると $(1)$ より $A' \in \mathcal{O}_X$ で、$x \in A'$ だから
\begin{equation*}
\mathrm{monad}_X(x) \subseteq {}^*A' \subseteq {}^*B' \subseteq {}^*B
\end{equation*}
である。$B \in \mathcal{N}_Y(x)$ は任意だから $\mathrm{monad}_X(x) \subseteq \mathrm{monad}_Y(x)$ であり、また $\mathrm{monad}_X(x) \subseteq {}^*X$ は明らかだから $\mathrm{monad}_X(x) \subseteq \mathrm{monad}_Y(x) \cap {}^*X$ が得られる。
逆に、任意に $A \in \mathcal{N}_X(x)$ をとると、$x \in A' \subseteq A$ となる $A' \in \mathcal{O}_X$ がとれ、$(1)$ よりある $B' \in \mathcal{O}_Y$ に対して $A' = B' \cap X$ となり、$x \in B'$ だから $\mathrm{monad}_Y(x) \subseteq {}^*B'$ より
\begin{equation*}
\mathrm{monad}_Y(x) \cap {}^*X \subseteq {}^*B' \cap {}^*X = {}^*A' \subseteq {}^*A
\end{equation*}
であり、$A \in \mathcal{N}_X(x)$ は任意だから $\mathrm{monad}_Y(x) \cap {}^*X \subseteq \mathrm{monad}_X(x)$ が得られる。
以上より $\mathrm{monad}_X(x) = \mathrm{monad}_Y(x) \cap {}^*X$ であり、$(2)$ が示された。
$(2) \Rightarrow (1)$ : $(2)$ が成り立つとし、任意に $A \in \mathscr{P}(X)$ をとる。
$A \in \mathcal{O}_X$ とする。$B' = A \cup (Y \setminus X)$ とおき、任意の $x \in A$ に対して $\mathrm{monad}_Y(x) \subseteq {}^*B'$ となることを示す。任意に $y \in \mathrm{monad}_Y(x)$ をとると、$y \in {}^*X$ ならば $(2)$ より
\begin{equation*}
y \in \mathrm{monad}_Y(x) \cap {}^*X = \mathrm{monad}_X(x) \subseteq {}^*A \subseteq {}^*B'
\end{equation*}
となるから $y \in {}^*B'$ である。$y \notin {}^*X$ ならば
\begin{equation*}
y \in {}^*Y \setminus {}^*X = {}^*(Y \setminus X) \subseteq {}^*B'
\end{equation*}
よりやはり $y \in {}^*B'$ である。これで $\mathrm{monad}_Y(x) \subseteq {}^*B'$ が示されたから $B' \in \mathcal{N}_Y(x)$ であり、$x \in B(x) \subseteq B'$ をみたす $B(x) \in \mathcal{O}_Y$ が存在する。$B = \bigcup_{x \in A}B(x)$ とおくと $B \in \mathcal{O}_Y$ かつ $B \subseteq B'$ で、明らかに $A \subseteq B \cap X$ であり、また $B \cap X \subseteq B' \cap X = A$ だから $A = B \cap X$ である。
逆に、ある $B \in \mathcal{O}_Y$ に対して $A = B \cap X$ ならば、任意の $x \in A$ に対して、$\mathrm{monad}_Y(x) \subseteq {}^*B$ と $(2)$ より
\begin{equation*}
\mathrm{monad}_X(x) = \mathrm{monad}_Y(x) \cap {}^*X \subseteq {}^*B \cap {}^*X = {}^*A
\end{equation*}
が得られるから、$A \in \mathcal{O}_X$ である。
以上より $A \in \mathcal{O}_X \leftrightarrow \exists B \in \mathcal{O}_Y \, (A = B \cap X)$ であり、$(1)$ が示された。□
さて、超準モデルを使って位相空間 $X$ を $X \subsetneq Y$ となる $Y$ に拡張する一つの方法を、次の補題によって示します。
【補題2】位相空間 $X$ と $X \subsetneq Y$ となる $Y$ があり、任意の $x \in Y \setminus X$ に対して $x \in \nu(x)$ をみたす $\nu(x) \in \mathscr{P}({}^*X)$ が定まっているとする。このとき任意の $x \in X$ に対して $\nu(x) = \mathrm{monad}_X(x)$ と定め、
\begin{equation*}
\mathcal{O}_Y = \{ \, A \in \mathscr{P}(Y) \, \mid \, \forall x \in A \, (\nu(x) \subseteq {}^*A) \, \}
\end{equation*}
で定まる開集合系 $\mathcal{O}_Y$ によって $Y$ に位相を定めると、
\begin{equation} \tag{3}
\forall x \in X \, (\mathrm{monad}_X(x) = \mathrm{monad}_Y(x))
\end{equation}
であり、従って【定理1】より $X$ は $Y$ の部分位相空間となる。
(証明)
任意に $x \in X$ をとる。まず、$\mathrm{monad}_X(x) = \nu(x) \subseteq \mathrm{monad}_Y(x)$ である。逆の包含関係を示すため、任意に $A \in \mathcal{N}_X(x)$ をとると、$x \in B \subseteq A$ となる $B \in \mathcal{O}_X$ が存在し、$\forall y \in B \, (\nu(y) = \mathrm{monad}_X(y) \subseteq {}^*B)$ より $B \in \mathcal{O}_Y$ となるから $A \in \mathcal{N}_Y(x)$ であり、これより $\mathrm{monad}_Y(x) \subseteq {}^*A$ である。$A \in \mathcal{N}_X(x)$ は任意だから $\mathrm{monad}_Y(x) \subseteq \mathrm{monad}_X(x)$ が得られる。以上で $(3)$ が示された。□
この補題の方法は、本来は $(2)$ でよいのにそれより強い $(3)$ が得られることから、位相空間の拡張手段としてはかなり「雑」といえます。しかし次に示す目的のためには、この方法で十分です。
2. アレクサンドロフの1点コンパクト化
ここまでの考察を利用して、「アレクサンドロフの1点コンパクト化」を超準モデルを用いて構成します。
位相空間 $X$ に対し、$X$ に属さない1点 $\infty$ を $X$ に追加した空間 $Y = X \cup \{ \infty \}$ を考え、次によって $\nu(\infty)$ を定めます。
\begin{equation*}
\nu(\infty) = \{ \, y \in {}^*X \, \mid \, \forall x \in X \, (y \notin \mathrm{monad}_X(x)) \, \} \cup \{ \infty \}
\end{equation*}
つまり「 ${}^*X$ のすべての遠標準点と $\infty$ を集めた集合」を $\nu(\infty)$ と定めます。
これを用いて【補題2】の方法で $X$ を部分位相空間とする $Y$ の位相が定まります。$(3)$ が成立するので、以下 $\mathrm{monad}$ の添字は省略します。
このとき、まず $Y$ はコンパクトです。なぜなら任意に $y \in {}^*Y$ をとると、$y$ はある $x \in X$ に対して $y \in \mathrm{monad}(x)$ となるか、または $y \in \nu(\infty)$ となるかのどちらかで、後者ならば $y \in \nu(\infty) \subseteq \mathrm{monad}(\infty)$ なので、第17回【定理5】より $Y$ はコンパクトになります。
次に、$X$ がコンパクトでない場合、$X$ は $Y$ において稠密となります。なぜなら $X$ がコンパクトでなければ ${}^*X$ は遠標準点をもつから $\nu(\infty) \cap {}^*X \neq \emptyset$ であり、従って $\mathrm{monad}(\infty) \cap {}^*X \neq \emptyset$ より $\forall x \in Y \, ( \mathrm{monad}(x) \cap {}^*X \neq \emptyset )$ となるから、第17回【定理3】の ix) より $X$ は $Y$ において稠密です。
これらの条件をみたす $Y = X \cup \{ \infty \}$ を $X$ のアレクサンドロフの1点コンパクト化といいます。従って上の方法は、任意のコンパクトでない位相空間から1点コンパクト化を構成する(超準モデルを使った)一つの方法を示しています。
さらに次が成り立ちます。
【補題3】$X$ がハウスドルフかつ局所コンパクト(任意の点に対してコンパクトな近傍が存在する)ならば、上の方法で構成した1点コンパクト化において、
\begin{equation*}
\mathrm{monad}(\infty) = \nu(\infty)
\end{equation*}
が成立する。
(証明)
$\mathrm{monad}(\infty) \supseteq \nu(\infty)$ は既に証明済み。$\mathrm{monad}(\infty) \subseteq \nu(\infty)$ を示すため、ある $ y \in \mathrm{monad}(\infty) \setminus \nu(\infty)$ が存在すると仮定して矛盾を導く。$y \notin \nu(\infty)$ なので、$\nu(\infty)$ の定義より、ある $x \in X$ に対して $y \in \mathrm{monad}(x)$ である。$X$ は局所コンパクトだから $A \in \mathcal{N}_X(x)$ となるコンパクトな $A$ が存在して $y \in \mathrm{monad}(x) \subseteq {}^*A$ より $y \in {}^*A$ となる。$X$ はハウスドルフだから第17回【定理6】 ii) より $A$ は $X$ の閉集合で、従って $X \setminus A$ は $X$ の開集合である。そこで $B = (X \setminus A) \cup \{ \infty \}$ とすると $B = Y \setminus A$ で、任意の $z \in X \setminus A$ に対して $\nu(z) = \mathrm{monad}(z) \subseteq {}^*(X \setminus A) \subseteq {}^*B$ である。また $A$ がコンパクトだから第17回【定理5】より ${}^*A$ の点は全て ${}^*X$ の近標準点で、$\nu(\infty)$ は ${}^*X$ の遠標準点と $\infty$ の集合だから $\nu(\infty) \cap {}^*A = \emptyset$ であり、これより $\nu(\infty) \subseteq {}^*Y \setminus {}^*A = {}^*(Y \setminus A) = {}^*B$ となる。従って $B$ は $Y$ における開集合であるから $\infty$ の近傍であり、 $y \in \mathrm{monad}(\infty) \subseteq {}^*B = {}^*Y \setminus {}^*A$ となるから $y \in {}^*A$ と矛盾する。以上より $\mathrm{monad}(\infty) \subseteq \nu(\infty)$ が得られたから $\mathrm{monad}(\infty) = \nu(\infty)$ である。□
この補題を使って、次の有名な結果が示されます。
【定理4】$X$ がハウスドルフかつ局所コンパクトのとき、上の方法で構成した1点コンパクト化はハウスドルフである。
(証明)
$X$ がハウスドルフであることと第17回【定理4】 ii) より、任意の $x, y \in X$ に対して $x \neq y \to \mathrm{monad}(x) \cap \mathrm{monad}(y) = \emptyset$ である。さらに【補題3】より $\mathrm{monad}(x) \cap \mathrm{monad}(\infty) = \mathrm{monad}(x) \cap \nu(\infty) = \emptyset$ も明らかなので、任意の $x, y \in Y$ に対して $x \neq y \to \mathrm{monad}(x) \cap \mathrm{monad}(y) = \emptyset$ が成り立ち、従って再び第17回【定理4】 ii) より $Y$ もハウスドルフである。□
ついでに、この定理の逆も超準モデルを利用して示しておきましょう。そのために必要になるのが次の補題です。
【補題5】位相空間 $X$ が $Y = X \cup \{ \infty \} \ ( \infty \notin X )$ の部分位相空間であり、かつ $Y$ が $\mathrm{T}_1$ ならば、次が成立する。
\begin{equation} \tag{4}
\forall x \in X \, (\mathrm{monad}_X(x) = \mathrm{monad}_Y(x))
\end{equation}
(証明)
【定理1】より任意の $x \in X$ に対して
\begin{equation*}
\mathrm{monad}_X(x) = \mathrm{monad}_Y(x) \cap {}^*X
\end{equation*}
が成立する。$Y$ が $\mathrm{T}_1$ だから第17回【定理4】 i) より $\infty \notin \mathrm{monad}_Y(x)$ であり、かつ ${}^*Y = {}^*X \cup \{ \infty \}$ だから $\mathrm{monad}_Y(x) \subseteq {}^*X$ すなわち $\mathrm{monad}_Y(x) \cap {}^*X = \mathrm{monad}_Y(x)$ である。従って $(4)$ が成立する。□
この補題を使って、【定理4】の逆が次のように示されます。
【定理6】$X$ の1点コンパクト化 $Y$ がハウスドルフならば、$X$ はハウスドルフかつ局所コンパクトである。
(証明)
$Y$ はハウスドルフだから $\mathrm{T}_1$ であり、【補題5】より $(4)$ が成立する。従って $Y$ のハウスドルフ性と第17回【定理4】 ii) より $X$ もハウスドルフである。任意に $x \in X$ をとると、$Y$ がハウスドルフだから $Y$ における $x$ の開近傍 $A$ と $\infty$ の開近傍 $B$ で $A \cap B = \emptyset$ となるものがとれる。$C = Y \setminus B$ とすると、$C$ はコンパクト空間 $Y$ の閉集合だから、第17回【定理6】 i) より $Y$ においてコンパクトである。従って第17回【定理5】より、
\begin{equation*}
\forall y \in {}^*C \, \exists z \in C \, (y \in \mathrm{monad}_Y(z))
\end{equation*}
が成立するが、$\infty \notin C$ より $C \subseteq X$ であり、これと $(4)$ より
\begin{equation*}
\forall y \in {}^*C \, \exists z \in C \, (y \in \mathrm{monad}_X(z))
\end{equation*}
が成立し、第17回【定理5】より $C$ は $X$ においてもコンパクトである。$A \subseteq C$ だから $C$ は $x$ のコンパクトな近傍であり、$x \in X$ は任意だから $X$ は局所コンパクトである。□
以上でアレクサンドロフの1点コンパクト化に関する諸定理が、超準モデルを使って証明されました。通常の方法に比べて特に簡単になるとは言えませんが、ハウスドルフ性やコンパクト性とモナドとの関係を見通しよく利用することができて、面白い方法だと思います。
(続く)(前記事)(目次)
わかってない奴がわかったつもりで書き留める超準解析(その17) [数学]
【超準解析について生半可な知識しかない僕が、わかったつもりの内容をちょっとずつ書き留めていきます。不正確な内容や誤りもあることをご承知ください。】
(17) 位相空間の超準的考察
第7回で距離空間を超準的に考察しましたが、本記事では一般の位相空間を超準的に考察することにします。位相空間の諸概念が簡単な論理式で表現できて、とても面白いです。
1. 上部構造と広大性原理
位相空間を超準的に考察するためには、超準モデルの「広大性原理」と呼ばれる性質が必要となります。まずこれを極めて雑にですが説明します。
$X$ を無限集合とし、適切な無限集合 $I$ とその上の超フィルターを使って、第6回で示した方法を使って $X$ から超冪 ${}^*X$ を構成します。同一視によって $X \subseteq {}^*X$ とみなし、${}^*X$ は $X$ の真の拡大とすることができます。
さらに考察の対象を広げて、$X$ から始めてその冪集合 $\mathscr{P}(X)$ との和集合 $X \cup \mathscr{P}(X)$ を作り、またその冪集合との和集合を作り、この作業を任意有限回繰り返してできる集合すべての和集合を $\mathcal{U}$ とします。これを「 $X$ の上部構造」と呼びます。また、 ${}^*X$ から始めて同様の操作で作られる「 ${}^*X$ の上部構造」を ${}^*\mathcal{U}$ とします。このとき $\mathcal{U}$ から ${}^*\mathcal{U}$ への写像 ${}^*$ を定義し、任意の $a \in \mathcal{U}$ に対して ${}^*a \in {}^*\mathcal{U}$ を対応させることができます。ただし $x \in X$ に対しては ${}^*x = x$ となります。
本稿ではこうして作った ${}^*\mathcal{U}$ を $\mathcal{U}$ の超準モデルとよび、$a$ に対する ${}^*a$ を $a$ の超準拡大とよぶこととします(あまり標準的なよび方ではないかもしれません)。
集合論言語の論理式 $\varphi(x_1, x_2, \cdots , x_n)$( $x_1, x_2, \cdots , x_n$ 以外に自由変数を持たない)と任意の $a_1, a_2, \cdots , a_n \in \mathcal{U}$ に対して、次の移行原理が成り立ちます。
ここでは「有界論理式」についての詳細は省略します。移行原理によって、任意の $X$ の部分集合 $A, B$ に対して、例えば ${}^*(A \cap B) = {}^*A \cap {}^*B$ や $A \subseteq B \Leftrightarrow {}^*A \subseteq {}^*B$ などの法則が示されます(第1回を参照)。
これに加え、超冪の構成で使用する $I$ とその上の超フィルターをうまくとると、次の広大性原理とよばれる性質が成り立ちます。
本記事では、超準モデルでは常に広大性原理が成立するものとします。
2. 位相空間の基本概念の超準的考察
$\langle X, \mathcal{O} \rangle$ を無限個の元をもつ位相空間とします。$\mathcal{O}$ は開集合系で、以降これを簡単に「位相空間 $X$」と呼びます。$x \in X, A \in \mathscr{P}(X)$ に対して $A$ が $x$ の近傍であるとは、$x \in B \subseteq A$ となる開集合 $B$ が存在することです。$x \in X$ に対して $x$ の近傍の全体を $\mathcal{N}(x)$ とかくこととします。
ここで、超準モデルを使ってモナドと呼ばれる次の集合を定義します。
必ず $x \in \mathrm{monad}(x)$ なので、これは空集合にはなりません。このとき次が成立します。
(証明)
$\Rightarrow$ の証明:モナドの定義から明らか。
$\Leftarrow$ の証明:$\mathrm{monad}(x) \subseteq {}^*A$ とし、$A \notin \mathcal{N}(x)$ を仮定して矛盾を導く。このとき任意の $B \in \mathcal{N}(x)$ に対して $B \not\subseteq A$ であるから $\exists y \in X \, (y \in B \setminus A)$ である。そこで、$\mathcal{N}(x) \times X$ 上の関係 $R$ を
\begin{equation*}
R = \{ \, \langle B, y \rangle \in \mathcal{N}(x) \times X \, \mid \, y \in B \setminus A \, \}
\end{equation*}
によって定めると、任意有限個の $B_1, B_2, \cdots , B_n \in \mathcal{N}(x)$ に対して $B_1 \cap B_2 \cap \cdots \cap B_n \in \mathcal{N}(x)$ だから、
\begin{equation*}
\exists y \in X \, (\langle B_1, y \rangle \in R \land \langle B_2, y \rangle \in R \land \cdots \land \langle B_n, y \rangle \in R)
\end{equation*}
が成り立ち、$R$ は有限共起的である。従って広大性原理によって
\begin{equation*}
\exists y \in {}^*X \, \forall B \in \mathcal{N}(x) \, (\langle {}^*B, y \rangle \in {}^*R)
\end{equation*}
すなわち
\begin{equation*}
\exists y \in {}^*X \, \forall B \in \mathcal{N}(x) \, (y \in {}^*B \setminus {}^*A)
\end{equation*}
が成り立つ。これより
\begin{equation*}
\exists y \in {}^*X \, (y \in \mathrm{monad}(x) \setminus {}^*A)
\end{equation*}
が従い、これは $\mathrm{monad}(x) \not\subseteq {}^*A$ を意味するから矛盾である。□
これを基本として、位相空間の様々な概念を超準モデルの論理式で表すことができます。
(証明)
i) $A$ が開集合 $\quad \Leftrightarrow \quad A$ が $A$ の各点 $x$ の近傍
$\quad \Leftrightarrow \quad \forall x \in A \, (\mathrm{monad}(x) \subseteq {}^*A)$
ii) $A$ が閉集合 $\quad \Leftrightarrow \quad X \setminus A$ が開集合
$\quad \Leftrightarrow \quad \forall x \in X \setminus A \, (\mathrm{monad}(x) \subseteq {}^*X \setminus {}^*A)$
$\quad \Leftrightarrow \quad \forall x \in X \, (x \notin A \to \mathrm{monad}(x) \cap {}^*A = \emptyset)$
$\quad \Leftrightarrow \quad \forall x \in X \, (\mathrm{monad}(x) \cap {}^*A \neq \emptyset \to x \in A)$
iii) $x$ が $A$ の内点 $\quad \Leftrightarrow \quad A$ が $x$ の近傍 $\quad \Leftrightarrow \quad \mathrm{monad}(x) \subseteq {}^*A$
iv) $x$ が $A$ の触点 $\quad \Leftrightarrow \quad x$ が $X \setminus A$ の内点でない $\quad \Leftrightarrow \quad \mathrm{monad}(x) \not\subseteq {}^*X \setminus {}^*A$
$\quad \Leftrightarrow \quad \mathrm{monad}(x) \cap {}^*A \neq \emptyset$
v) $x$ が $A$ の境界点 $\quad \Leftrightarrow \quad x$ が $A$ と $X \setminus A$ の両方の触点
$\quad \Leftrightarrow \quad \mathrm{monad}(x) \cap {}^*A \neq \emptyset \land \mathrm{monad}(x) \cap ({}^*X \setminus {}^*A) \neq \emptyset$
vi) $x$ が $A$ の孤立点 $\quad \Leftrightarrow \quad \exists B \in \mathcal{N}(x) \, (B \cap A = \{ x \} )$
$\quad \Leftrightarrow \quad \exists B \in \mathcal{N}(x) \, (B \subseteq (X \setminus A) \cup \{ x \} \land x \in A)$
$\quad \Leftrightarrow \quad \exists B \in \mathcal{N}(x) \, ({}^*B \subseteq ({}^*X \setminus {}^*A) \cup \{ x \} \land x \in {}^*A)$ (移行原理)
$\quad \Leftrightarrow \quad \exists B \in \mathscr{P}(X) \, (\mathrm{monad}(x) \subseteq {}^*B \subseteq ({}^*X \setminus {}^*A) \cup \{ x \} \land x \in {}^*A)$
$\quad \Leftrightarrow \quad \mathrm{monad}(x) \subseteq ({}^*X \setminus {}^*A) \cup \{ x \} \land x \in {}^*A$
$\quad \Leftrightarrow \quad \mathrm{monad}(x) \cap {}^*A = \{ x \}$
vii) $x$ が $A$ の集積点 $\quad \Leftrightarrow \quad$ $x$ が $A$ の触点であり、かつ孤立点でない
$\quad \Leftrightarrow \quad \mathrm{monad}(x) \cap {}^*A \neq \emptyset \land \mathrm{monad}(x) \cap {}^*A \neq \{ x \}$
$\quad \Leftrightarrow \quad ( \mathrm{monad}(x) \cap {}^*A) \setminus \{ x \} \neq \emptyset$
viii) $A$ が自己稠密 $\quad \Leftrightarrow \quad A$ の各点が $A$ の集積点
$\quad \Leftrightarrow \quad \forall x \in A \, ( ( \mathrm{monad}(x) \cap {}^*A) \setminus \{ x \} \neq \emptyset )$
ix) $A$ が $X$ において稠密 $\quad \Leftrightarrow \quad X$ の各点が $A$ の触点
$\quad \Leftrightarrow \quad \forall x \in X \, ( \mathrm{monad}(x) \cap {}^*A \neq \emptyset )$
□
【定理3】の表の論理式は、第7回で紹介した距離空間における表の右側欄と同じになっていることがわかります。距離空間は位相空間の特別なものなので、この結果は整合が取れています。
3. 分離公理とコンパクト性
2種類の分離公理について、超準モデルによる同値条件を示します。
(証明)
i) $X$ が $\mathrm{T}_1$ である
$\quad \Leftrightarrow \quad \forall x, y \in X \, (x \neq y \to \exists A \in \mathcal{N}(x) \, (y \notin A) \land \exists B \in \mathcal{N}(y) \, (x \notin B))$
$\quad \Leftrightarrow \quad \forall x, y \in X \, (x \neq y \to \exists A \in \mathcal{N}(x) \, (y \notin {}^*A) \land \exists B \in \mathcal{N}(y) \, (x \notin {}^*B))$ (移行原理)
$\quad \Leftrightarrow \quad \forall x, y \in X \, (x \neq y \to y \notin \mathrm{monad}(x) \land x \notin \mathrm{monad}(y))$
ii) $X$ が $\mathrm{T}_2$(ハウスドルフ)である
$\quad \Leftrightarrow \quad \forall x, y \in X \, (x \neq y \to \exists A \in \mathcal{N}(x) \, \exists B \in \mathcal{N}(y) \, (A \cap B = \emptyset))$
$\quad \Leftrightarrow \quad \forall x, y \in X \, (x \neq y \to \exists A \in \mathcal{N}(x) \, \exists B \in \mathcal{N}(y) \, ({}^*A \cap {}^*B = \emptyset))$ (移行原理)
$\quad \Rightarrow \quad \forall x, y \in X \, (x \neq y \to \mathrm{monad}(x) \cap \mathrm{monad}(y) = \emptyset )$
逆に $\forall x, y \in X \, (x \neq y \to \mathrm{monad}(x) \cap \mathrm{monad}(y) = \emptyset )$ かつ $X$ がハウスドルフでないと仮定すると、ある $x, y \in X, x \neq y$ が存在して、
\begin{equation*}
\forall A \in \mathcal{N}(x) \, \forall B \in \mathcal{N}(y) \, (A \cap B \neq \emptyset))
\end{equation*}
すなわち
\begin{equation*}
\forall A \in \mathcal{N}(x) \, \forall B \in \mathcal{N}(y) \, \exists z \in X \, (z \in A \cap B)
\end{equation*}
となる。そこで $(\mathcal{N}(x) \times \mathcal{N}(y)) \times X$ 上の関係 $R$ を、
\begin{equation*}
R = \{ \, \langle \langle A, B \rangle , z \rangle \in (\mathcal{N}(x) \times \mathcal{N}(y)) \times X \, \mid \, z \in A \cap B \, \}
\end{equation*}
によって定めると、$R$ は明らかに有限共起的だから、広大性原理によって、
\begin{equation*}
\exists z \in {}^*X \, \forall A \in \mathcal{N}(x) \, \forall B \in \mathcal{N}(y) \, (z \in {}^*A \cap {}^*B)
\end{equation*}
が成り立つ。よって $\exists z \in {}^*X \, (z \in \mathrm{monad}(x) \cap \mathrm{monad}(y))$ となるが、これは $\mathrm{monad}(x) \cap \mathrm{monad}(y) = \emptyset$ と矛盾する。よって、
$\forall x, y \in X \, (x \neq y \to \mathrm{monad}(x) \cap \mathrm{monad}(y) = \emptyset ) \quad \Rightarrow \quad X$ が$\mathrm{T}_2$(ハウスドルフ)である
□
この定理より、$\mathrm{T}_1$ 空間は「どの点も他の点のモナドに属さない空間」、ハウスドルフ空間は「異なる点のモナドが交わらない空間」とイメージできます。特にハウスドルフ空間を簡単に言うと「モナドがダブらない空間」です。
また、コンパクト性については、次の非常に簡明な同値条件があります。
(証明)
$\Rightarrow$ の証明:$A$ がコンパクトとする。$\exists y \in {}^*A \, \forall x \in A \, (y \notin \mathrm{monad}(x))$ を仮定して矛盾を導く。これをみたす $y$ をとると、任意の $x \in A$ に対して開近傍 $B(x) \in \mathcal{N}(x) \cap \mathcal{O}$ が存在して $y \notin {}^*B(x)$ となる。すると、
\begin{equation*}
\{ \, B(x) \, \mid \, x \in A \, \}
\end{equation*}
は $A$ の開被覆であり、$A$ はコンパクトだから有限個の $x_1, x_2, \cdots , x_n$ がとれて、
\begin{equation*}
A \subseteq B(x_1) \cup B(x_2) \cup \cdots \cup B(x_n)
\end{equation*}
とすることができる。移行原理より、
\begin{equation*}
{}^*A \subseteq {}^*B(x_1) \cup {}^*B(x_2) \cup \cdots \cup {}^*B(x_n)
\end{equation*}
かつ $y \notin {}^*B(x_1) \cup {}^*B(x_2) \cup \cdots \cup {}^*B(x_n)$ だから $y \notin {}^*A$ となるが、これは矛盾である。
$\Leftarrow$ の証明:$\forall y \in {}^*A \, \exists x \in A \, (y \in \mathrm{monad}(x))$ とする。$A$ がコンパクトでないと仮定して矛盾を導く。$A$ の開被覆 $\mathcal{C}$ で、有限個の元をどのようにとっても $A$ の被覆にならないものが存在する。このとき $\mathcal{C} \times A$ 上の関係 $R$ を、
\begin{equation*}
R = \{ \, \langle B, y \rangle \in \mathcal{C} \times A \, \mid \, y \notin B \, \}
\end{equation*}
によって定めると、任意有限個の $B_1, B_2, \cdots , B_n \in \mathcal{C}$ に対して $A \setminus (B_1 \cup B_2 \cup \cdots \cup B_n) \neq \emptyset$ だから、
\begin{equation*}
\exists y \in A \, (\langle B_1, y \rangle \in R \land \langle B_2, y \rangle \in R \land \cdots \land \langle B_n, y \rangle \in R)
\end{equation*}
となって $R$ は有限共起的である。従って広大性原理より、
\begin{equation*}
\exists y \in {}^*A \, \forall B \in \mathcal{C} \, (\langle {}^*B, y \rangle \in {}^*R)
\end{equation*}
すなわち
\begin{equation*}
\exists y \in {}^*A \, \forall B \in \mathcal{C} \, (y \notin {}^*B)
\end{equation*}
である。これをみたす $y$ をとると、$y \in \mathrm{monad}(x)$ となる $x \in A$ が存在し、この $x$ に対し $x \in B_0 \in \mathcal{C}$ となる開集合 $B_0$ が存在するから、
\begin{equation*}
y \in \mathrm{monad}(x) \subseteq {}^*B_0
\end{equation*}
すなわち $y \in {}^*B_0$ となるが、一方で $\forall B \in \mathcal{C} \, (y \notin {}^*B)$ より $y \notin {}^*B_0$ だから矛盾である。□
この定理より、コンパクト集合は「超準拡大が各点のモナドで覆い切れる集合」とイメージできます。もっと簡単に言うと「モナドに漏れがない集合」です。この結果も第8回の距離空間に関する結果と整合が取れていることがわかります。
そうすると、ハウスドルフでかつコンパクトな位相空間は「モナドにダブリも漏れもない空間」、どこかで聞いた用語を使うと「モナドがMECEな空間」となります。イメージしやすいですね。
これらの同値条件を使うと、例えば次の定理が論理式を使った簡単な考察だけで証明できます。
(証明)
i) 任意に $y \in {}^*A$ をとる。$X$ がコンパクトだから【定理5】より $y \in \mathrm{monad}(x)$ となる $x \in X$ が存在する。$y \in \mathrm{monad}(x) \cap {}^*A$ すなわち $\mathrm{monad}(x) \cap {}^*A \neq \emptyset$ で、$A$ は閉集合だから、【定理3】ii) より $x \in A$ となる。従って $\forall y \in {}^*A \, \exists x \in A \, (y \in \mathrm{monad}(x))$ であるから、再び【定理5】より $A$ はコンパクトである。
ii) 任意に $\mathrm{monad}(x) \cap {}^*A \neq \emptyset$ をみたす $x \in X$ をとる。$y \in \mathrm{monad}(x) \cap {}^*A$ をとると、$A$ がコンパクトだから【定理5】より $y \in \mathrm{monad}(x')$ となる $x' \in A$ がある。$\mathrm{monad}(x) \cap \mathrm{monad}(x') \neq \emptyset$ で $X$ がハウスドルフだから、【定理4】ii) より $x = x'$ であり、これより $x \in A$ となる。従って【定理3】ii) より $A$ は閉集合である。
□
なお、$\exists x \in X \, (y \in \mathrm{monad}(x))$ をみたす $y \in {}^*X$ を ${}^*X$ の近標準点といい、そうでない $y \in {}^*X$ を ${}^*X$ の遠標準点といいます。この用語を使うと、空間 $X$ 自身がコンパクトであることは「すべての ${}^*X$ の点が近標準点である」ことと同値です。
[参考文献]
中村 徹『超準解析と物理学(増補改訂版)』(日本評論社, 2017)
(続く)(前記事)(目次)
(17) 位相空間の超準的考察
第7回で距離空間を超準的に考察しましたが、本記事では一般の位相空間を超準的に考察することにします。位相空間の諸概念が簡単な論理式で表現できて、とても面白いです。
1. 上部構造と広大性原理
位相空間を超準的に考察するためには、超準モデルの「広大性原理」と呼ばれる性質が必要となります。まずこれを極めて雑にですが説明します。
$X$ を無限集合とし、適切な無限集合 $I$ とその上の超フィルターを使って、第6回で示した方法を使って $X$ から超冪 ${}^*X$ を構成します。同一視によって $X \subseteq {}^*X$ とみなし、${}^*X$ は $X$ の真の拡大とすることができます。
さらに考察の対象を広げて、$X$ から始めてその冪集合 $\mathscr{P}(X)$ との和集合 $X \cup \mathscr{P}(X)$ を作り、またその冪集合との和集合を作り、この作業を任意有限回繰り返してできる集合すべての和集合を $\mathcal{U}$ とします。これを「 $X$ の上部構造」と呼びます。また、 ${}^*X$ から始めて同様の操作で作られる「 ${}^*X$ の上部構造」を ${}^*\mathcal{U}$ とします。このとき $\mathcal{U}$ から ${}^*\mathcal{U}$ への写像 ${}^*$ を定義し、任意の $a \in \mathcal{U}$ に対して ${}^*a \in {}^*\mathcal{U}$ を対応させることができます。ただし $x \in X$ に対しては ${}^*x = x$ となります。
本稿ではこうして作った ${}^*\mathcal{U}$ を $\mathcal{U}$ の超準モデルとよび、$a$ に対する ${}^*a$ を $a$ の超準拡大とよぶこととします(あまり標準的なよび方ではないかもしれません)。
集合論言語の論理式 $\varphi(x_1, x_2, \cdots , x_n)$( $x_1, x_2, \cdots , x_n$ 以外に自由変数を持たない)と任意の $a_1, a_2, \cdots , a_n \in \mathcal{U}$ に対して、次の移行原理が成り立ちます。
【移行原理】
$\varphi(x_1, x_2, \cdots , x_n)$ が有界論理式のとき、$\mathcal{U}$ 上で \begin{equation*} \varphi(a_1, a_2, \cdots , a_n) \end{equation*} が成り立つことと、${}^*\mathcal{U}$ 上で \begin{equation*} \varphi({}^*a_1, {}^*a_2, \cdots , {}^*a_n) \end{equation*} が成り立つことは同値である。
$\varphi(x_1, x_2, \cdots , x_n)$ が有界論理式のとき、$\mathcal{U}$ 上で \begin{equation*} \varphi(a_1, a_2, \cdots , a_n) \end{equation*} が成り立つことと、${}^*\mathcal{U}$ 上で \begin{equation*} \varphi({}^*a_1, {}^*a_2, \cdots , {}^*a_n) \end{equation*} が成り立つことは同値である。
ここでは「有界論理式」についての詳細は省略します。移行原理によって、任意の $X$ の部分集合 $A, B$ に対して、例えば ${}^*(A \cap B) = {}^*A \cap {}^*B$ や $A \subseteq B \Leftrightarrow {}^*A \subseteq {}^*B$ などの法則が示されます(第1回を参照)。
これに加え、超冪の構成で使用する $I$ とその上の超フィルターをうまくとると、次の広大性原理とよばれる性質が成り立ちます。
【広大性原理】
$\mathcal{U}$ 上の2項関係 $R \, (\subseteq A \times B, \ A, B \in \mathcal{U})$ が有限共起的であるとする。すなわち任意にとった有限個の $a_1, a_2, \cdots , a_n \in \mathrm{Dom}(R) \subseteq A$ に対して、$\mathcal{U}$ 上で \begin{equation*} \exists b \in B \, (\langle a_1, b \rangle \in R \land \langle a_2, b \rangle \in R \land \cdots \land \langle a_n, b \rangle \in R) \end{equation*} が成り立つとする。このとき ${}^*\mathcal{U}$ 上で次が成り立つ。 \begin{equation*} \exists b \in {}^*B \, \forall a \in \mathrm{Dom}(R) \, (\langle {}^*a, b \rangle \in {}^*R) \end{equation*}
$\mathcal{U}$ 上の2項関係 $R \, (\subseteq A \times B, \ A, B \in \mathcal{U})$ が有限共起的であるとする。すなわち任意にとった有限個の $a_1, a_2, \cdots , a_n \in \mathrm{Dom}(R) \subseteq A$ に対して、$\mathcal{U}$ 上で \begin{equation*} \exists b \in B \, (\langle a_1, b \rangle \in R \land \langle a_2, b \rangle \in R \land \cdots \land \langle a_n, b \rangle \in R) \end{equation*} が成り立つとする。このとき ${}^*\mathcal{U}$ 上で次が成り立つ。 \begin{equation*} \exists b \in {}^*B \, \forall a \in \mathrm{Dom}(R) \, (\langle {}^*a, b \rangle \in {}^*R) \end{equation*}
本記事では、超準モデルでは常に広大性原理が成立するものとします。
2. 位相空間の基本概念の超準的考察
$\langle X, \mathcal{O} \rangle$ を無限個の元をもつ位相空間とします。$\mathcal{O}$ は開集合系で、以降これを簡単に「位相空間 $X$」と呼びます。$x \in X, A \in \mathscr{P}(X)$ に対して $A$ が $x$ の近傍であるとは、$x \in B \subseteq A$ となる開集合 $B$ が存在することです。$x \in X$ に対して $x$ の近傍の全体を $\mathcal{N}(x)$ とかくこととします。
ここで、超準モデルを使ってモナドと呼ばれる次の集合を定義します。
【定義1】(モナド)
$x \in X$ に対し、次によって定まる $^*X$ の部分集合 $\mathrm{monad}(x)$ を「$x$ のモナド」と呼ぶ。 \begin{equation*} \mathrm{monad}(x) = \bigcap \{ \, {}^*A \, \mid \, A \in \mathcal{N}(x) \, \} \end{equation*}
$x \in X$ に対し、次によって定まる $^*X$ の部分集合 $\mathrm{monad}(x)$ を「$x$ のモナド」と呼ぶ。 \begin{equation*} \mathrm{monad}(x) = \bigcap \{ \, {}^*A \, \mid \, A \in \mathcal{N}(x) \, \} \end{equation*}
必ず $x \in \mathrm{monad}(x)$ なので、これは空集合にはなりません。このとき次が成立します。
【定理2】(近傍の超準モデルによる同値条件)
$x \in X, A \in \mathscr{P}(X)$ に対して、次が成立する。 \begin{equation*} A \in \mathcal{N}(x) \quad \Leftrightarrow \quad \mathrm{monad}(x) \subseteq {}^*A \end{equation*}
$x \in X, A \in \mathscr{P}(X)$ に対して、次が成立する。 \begin{equation*} A \in \mathcal{N}(x) \quad \Leftrightarrow \quad \mathrm{monad}(x) \subseteq {}^*A \end{equation*}
(証明)
$\Rightarrow$ の証明:モナドの定義から明らか。
$\Leftarrow$ の証明:$\mathrm{monad}(x) \subseteq {}^*A$ とし、$A \notin \mathcal{N}(x)$ を仮定して矛盾を導く。このとき任意の $B \in \mathcal{N}(x)$ に対して $B \not\subseteq A$ であるから $\exists y \in X \, (y \in B \setminus A)$ である。そこで、$\mathcal{N}(x) \times X$ 上の関係 $R$ を
\begin{equation*}
R = \{ \, \langle B, y \rangle \in \mathcal{N}(x) \times X \, \mid \, y \in B \setminus A \, \}
\end{equation*}
によって定めると、任意有限個の $B_1, B_2, \cdots , B_n \in \mathcal{N}(x)$ に対して $B_1 \cap B_2 \cap \cdots \cap B_n \in \mathcal{N}(x)$ だから、
\begin{equation*}
\exists y \in X \, (\langle B_1, y \rangle \in R \land \langle B_2, y \rangle \in R \land \cdots \land \langle B_n, y \rangle \in R)
\end{equation*}
が成り立ち、$R$ は有限共起的である。従って広大性原理によって
\begin{equation*}
\exists y \in {}^*X \, \forall B \in \mathcal{N}(x) \, (\langle {}^*B, y \rangle \in {}^*R)
\end{equation*}
すなわち
\begin{equation*}
\exists y \in {}^*X \, \forall B \in \mathcal{N}(x) \, (y \in {}^*B \setminus {}^*A)
\end{equation*}
が成り立つ。これより
\begin{equation*}
\exists y \in {}^*X \, (y \in \mathrm{monad}(x) \setminus {}^*A)
\end{equation*}
が従い、これは $\mathrm{monad}(x) \not\subseteq {}^*A$ を意味するから矛盾である。□
これを基本として、位相空間の様々な概念を超準モデルの論理式で表すことができます。
【定理3】(位相空間の諸概念の超準モデルによる同値条件)
$x \in X, A \in \mathscr{P}(X)$ に対して、次表の同値な対応関係が成立する。
$x \in X, A \in \mathscr{P}(X)$ に対して、次表の同値な対応関係が成立する。
| 位相的概念 | 超準モデル上の同値条件 | |
|---|---|---|
| i) | $A$ が開集合 | $\forall x \in A \, (\mathrm{monad}(x) \subseteq {}^*A)$ |
| ii) | $A$ が閉集合 | $\forall x \in X \, (\mathrm{monad}(x) \cap {}^*A \neq \emptyset \to x \in A)$ |
| iii) | $x$ が $A$ の内点 | $\mathrm{monad}(x) \subseteq {}^*A$ |
| iv) | $x$ が $A$ の触点 | $\mathrm{monad}(x) \cap {}^*A \neq \emptyset$ |
| v) | $x$ が $A$ の境界点 | $\mathrm{monad}(x) \cap {}^*A \neq \emptyset \land \mathrm{monad}(x) \cap ({}^*X \setminus {}^*A) \neq \emptyset$ |
| vi) | $x$ が $A$ の孤立点 | $\mathrm{monad}(x) \cap {}^*A = \{ x \}$ |
| vii) | $x$ が $A$ の集積点 | $(\mathrm{monad}(x) \cap {}^*A) \setminus \{x\} \neq \emptyset$ |
| viii) | $A$ が自己稠密 | $\forall x \in A \, ((\mathrm{monad}(x) \cap {}^*A) \setminus \{x\} \neq \emptyset)$ |
| ix) | $A$ が $X$ において稠密 | $\forall x \in X \, (\mathrm{monad}(x) \cap {}^*A \neq \emptyset)$ |
(証明)
i) $A$ が開集合 $\quad \Leftrightarrow \quad A$ が $A$ の各点 $x$ の近傍
$\quad \Leftrightarrow \quad \forall x \in A \, (\mathrm{monad}(x) \subseteq {}^*A)$
ii) $A$ が閉集合 $\quad \Leftrightarrow \quad X \setminus A$ が開集合
$\quad \Leftrightarrow \quad \forall x \in X \setminus A \, (\mathrm{monad}(x) \subseteq {}^*X \setminus {}^*A)$
$\quad \Leftrightarrow \quad \forall x \in X \, (x \notin A \to \mathrm{monad}(x) \cap {}^*A = \emptyset)$
$\quad \Leftrightarrow \quad \forall x \in X \, (\mathrm{monad}(x) \cap {}^*A \neq \emptyset \to x \in A)$
iii) $x$ が $A$ の内点 $\quad \Leftrightarrow \quad A$ が $x$ の近傍 $\quad \Leftrightarrow \quad \mathrm{monad}(x) \subseteq {}^*A$
iv) $x$ が $A$ の触点 $\quad \Leftrightarrow \quad x$ が $X \setminus A$ の内点でない $\quad \Leftrightarrow \quad \mathrm{monad}(x) \not\subseteq {}^*X \setminus {}^*A$
$\quad \Leftrightarrow \quad \mathrm{monad}(x) \cap {}^*A \neq \emptyset$
v) $x$ が $A$ の境界点 $\quad \Leftrightarrow \quad x$ が $A$ と $X \setminus A$ の両方の触点
$\quad \Leftrightarrow \quad \mathrm{monad}(x) \cap {}^*A \neq \emptyset \land \mathrm{monad}(x) \cap ({}^*X \setminus {}^*A) \neq \emptyset$
vi) $x$ が $A$ の孤立点 $\quad \Leftrightarrow \quad \exists B \in \mathcal{N}(x) \, (B \cap A = \{ x \} )$
$\quad \Leftrightarrow \quad \exists B \in \mathcal{N}(x) \, (B \subseteq (X \setminus A) \cup \{ x \} \land x \in A)$
$\quad \Leftrightarrow \quad \exists B \in \mathcal{N}(x) \, ({}^*B \subseteq ({}^*X \setminus {}^*A) \cup \{ x \} \land x \in {}^*A)$ (移行原理)
$\quad \Leftrightarrow \quad \exists B \in \mathscr{P}(X) \, (\mathrm{monad}(x) \subseteq {}^*B \subseteq ({}^*X \setminus {}^*A) \cup \{ x \} \land x \in {}^*A)$
$\quad \Leftrightarrow \quad \mathrm{monad}(x) \subseteq ({}^*X \setminus {}^*A) \cup \{ x \} \land x \in {}^*A$
$\quad \Leftrightarrow \quad \mathrm{monad}(x) \cap {}^*A = \{ x \}$
vii) $x$ が $A$ の集積点 $\quad \Leftrightarrow \quad$ $x$ が $A$ の触点であり、かつ孤立点でない
$\quad \Leftrightarrow \quad \mathrm{monad}(x) \cap {}^*A \neq \emptyset \land \mathrm{monad}(x) \cap {}^*A \neq \{ x \}$
$\quad \Leftrightarrow \quad ( \mathrm{monad}(x) \cap {}^*A) \setminus \{ x \} \neq \emptyset$
viii) $A$ が自己稠密 $\quad \Leftrightarrow \quad A$ の各点が $A$ の集積点
$\quad \Leftrightarrow \quad \forall x \in A \, ( ( \mathrm{monad}(x) \cap {}^*A) \setminus \{ x \} \neq \emptyset )$
ix) $A$ が $X$ において稠密 $\quad \Leftrightarrow \quad X$ の各点が $A$ の触点
$\quad \Leftrightarrow \quad \forall x \in X \, ( \mathrm{monad}(x) \cap {}^*A \neq \emptyset )$
□
【定理3】の表の論理式は、第7回で紹介した距離空間における表の右側欄と同じになっていることがわかります。距離空間は位相空間の特別なものなので、この結果は整合が取れています。
3. 分離公理とコンパクト性
2種類の分離公理について、超準モデルによる同値条件を示します。
【定理4】($\mathrm{T}_1, \mathrm{T}_2$ 分離公理の超準モデルによる同値条件)
i) $X$ が $\mathrm{T}_1$ である $\quad \Leftrightarrow \quad \forall x, y \in X \, (x \neq y \to y \notin \mathrm{monad}(x) \land x \notin \mathrm{monad}(y))$
ii) $X$ が $\mathrm{T}_2$(ハウスドルフ)である $\quad \Leftrightarrow \quad \forall x, y \in X \, (x \neq y \to \mathrm{monad}(x) \cap \mathrm{monad}(y) = \emptyset )$
i) $X$ が $\mathrm{T}_1$ である $\quad \Leftrightarrow \quad \forall x, y \in X \, (x \neq y \to y \notin \mathrm{monad}(x) \land x \notin \mathrm{monad}(y))$
ii) $X$ が $\mathrm{T}_2$(ハウスドルフ)である $\quad \Leftrightarrow \quad \forall x, y \in X \, (x \neq y \to \mathrm{monad}(x) \cap \mathrm{monad}(y) = \emptyset )$
(証明)
i) $X$ が $\mathrm{T}_1$ である
$\quad \Leftrightarrow \quad \forall x, y \in X \, (x \neq y \to \exists A \in \mathcal{N}(x) \, (y \notin A) \land \exists B \in \mathcal{N}(y) \, (x \notin B))$
$\quad \Leftrightarrow \quad \forall x, y \in X \, (x \neq y \to \exists A \in \mathcal{N}(x) \, (y \notin {}^*A) \land \exists B \in \mathcal{N}(y) \, (x \notin {}^*B))$ (移行原理)
$\quad \Leftrightarrow \quad \forall x, y \in X \, (x \neq y \to y \notin \mathrm{monad}(x) \land x \notin \mathrm{monad}(y))$
ii) $X$ が $\mathrm{T}_2$(ハウスドルフ)である
$\quad \Leftrightarrow \quad \forall x, y \in X \, (x \neq y \to \exists A \in \mathcal{N}(x) \, \exists B \in \mathcal{N}(y) \, (A \cap B = \emptyset))$
$\quad \Leftrightarrow \quad \forall x, y \in X \, (x \neq y \to \exists A \in \mathcal{N}(x) \, \exists B \in \mathcal{N}(y) \, ({}^*A \cap {}^*B = \emptyset))$ (移行原理)
$\quad \Rightarrow \quad \forall x, y \in X \, (x \neq y \to \mathrm{monad}(x) \cap \mathrm{monad}(y) = \emptyset )$
逆に $\forall x, y \in X \, (x \neq y \to \mathrm{monad}(x) \cap \mathrm{monad}(y) = \emptyset )$ かつ $X$ がハウスドルフでないと仮定すると、ある $x, y \in X, x \neq y$ が存在して、
\begin{equation*}
\forall A \in \mathcal{N}(x) \, \forall B \in \mathcal{N}(y) \, (A \cap B \neq \emptyset))
\end{equation*}
すなわち
\begin{equation*}
\forall A \in \mathcal{N}(x) \, \forall B \in \mathcal{N}(y) \, \exists z \in X \, (z \in A \cap B)
\end{equation*}
となる。そこで $(\mathcal{N}(x) \times \mathcal{N}(y)) \times X$ 上の関係 $R$ を、
\begin{equation*}
R = \{ \, \langle \langle A, B \rangle , z \rangle \in (\mathcal{N}(x) \times \mathcal{N}(y)) \times X \, \mid \, z \in A \cap B \, \}
\end{equation*}
によって定めると、$R$ は明らかに有限共起的だから、広大性原理によって、
\begin{equation*}
\exists z \in {}^*X \, \forall A \in \mathcal{N}(x) \, \forall B \in \mathcal{N}(y) \, (z \in {}^*A \cap {}^*B)
\end{equation*}
が成り立つ。よって $\exists z \in {}^*X \, (z \in \mathrm{monad}(x) \cap \mathrm{monad}(y))$ となるが、これは $\mathrm{monad}(x) \cap \mathrm{monad}(y) = \emptyset$ と矛盾する。よって、
$\forall x, y \in X \, (x \neq y \to \mathrm{monad}(x) \cap \mathrm{monad}(y) = \emptyset ) \quad \Rightarrow \quad X$ が$\mathrm{T}_2$(ハウスドルフ)である
□
この定理より、$\mathrm{T}_1$ 空間は「どの点も他の点のモナドに属さない空間」、ハウスドルフ空間は「異なる点のモナドが交わらない空間」とイメージできます。特にハウスドルフ空間を簡単に言うと「モナドがダブらない空間」です。
また、コンパクト性については、次の非常に簡明な同値条件があります。
【定理5】(コンパクト性の超準モデルによる同値条件)
$A \subseteq X$ とすると、次が成立する。
$A \subseteq X$ とすると、次が成立する。
$A$ がコンパクトである $\quad \Leftrightarrow \quad \forall y \in {}^*A \, \exists x \in A \, (y \in \mathrm{monad}(x))$
(証明)
$\Rightarrow$ の証明:$A$ がコンパクトとする。$\exists y \in {}^*A \, \forall x \in A \, (y \notin \mathrm{monad}(x))$ を仮定して矛盾を導く。これをみたす $y$ をとると、任意の $x \in A$ に対して開近傍 $B(x) \in \mathcal{N}(x) \cap \mathcal{O}$ が存在して $y \notin {}^*B(x)$ となる。すると、
\begin{equation*}
\{ \, B(x) \, \mid \, x \in A \, \}
\end{equation*}
は $A$ の開被覆であり、$A$ はコンパクトだから有限個の $x_1, x_2, \cdots , x_n$ がとれて、
\begin{equation*}
A \subseteq B(x_1) \cup B(x_2) \cup \cdots \cup B(x_n)
\end{equation*}
とすることができる。移行原理より、
\begin{equation*}
{}^*A \subseteq {}^*B(x_1) \cup {}^*B(x_2) \cup \cdots \cup {}^*B(x_n)
\end{equation*}
かつ $y \notin {}^*B(x_1) \cup {}^*B(x_2) \cup \cdots \cup {}^*B(x_n)$ だから $y \notin {}^*A$ となるが、これは矛盾である。
$\Leftarrow$ の証明:$\forall y \in {}^*A \, \exists x \in A \, (y \in \mathrm{monad}(x))$ とする。$A$ がコンパクトでないと仮定して矛盾を導く。$A$ の開被覆 $\mathcal{C}$ で、有限個の元をどのようにとっても $A$ の被覆にならないものが存在する。このとき $\mathcal{C} \times A$ 上の関係 $R$ を、
\begin{equation*}
R = \{ \, \langle B, y \rangle \in \mathcal{C} \times A \, \mid \, y \notin B \, \}
\end{equation*}
によって定めると、任意有限個の $B_1, B_2, \cdots , B_n \in \mathcal{C}$ に対して $A \setminus (B_1 \cup B_2 \cup \cdots \cup B_n) \neq \emptyset$ だから、
\begin{equation*}
\exists y \in A \, (\langle B_1, y \rangle \in R \land \langle B_2, y \rangle \in R \land \cdots \land \langle B_n, y \rangle \in R)
\end{equation*}
となって $R$ は有限共起的である。従って広大性原理より、
\begin{equation*}
\exists y \in {}^*A \, \forall B \in \mathcal{C} \, (\langle {}^*B, y \rangle \in {}^*R)
\end{equation*}
すなわち
\begin{equation*}
\exists y \in {}^*A \, \forall B \in \mathcal{C} \, (y \notin {}^*B)
\end{equation*}
である。これをみたす $y$ をとると、$y \in \mathrm{monad}(x)$ となる $x \in A$ が存在し、この $x$ に対し $x \in B_0 \in \mathcal{C}$ となる開集合 $B_0$ が存在するから、
\begin{equation*}
y \in \mathrm{monad}(x) \subseteq {}^*B_0
\end{equation*}
すなわち $y \in {}^*B_0$ となるが、一方で $\forall B \in \mathcal{C} \, (y \notin {}^*B)$ より $y \notin {}^*B_0$ だから矛盾である。□
この定理より、コンパクト集合は「超準拡大が各点のモナドで覆い切れる集合」とイメージできます。もっと簡単に言うと「モナドに漏れがない集合」です。この結果も第8回の距離空間に関する結果と整合が取れていることがわかります。
そうすると、ハウスドルフでかつコンパクトな位相空間は「モナドにダブリも漏れもない空間」、どこかで聞いた用語を使うと「モナドがMECEな空間」となります。イメージしやすいですね。
これらの同値条件を使うと、例えば次の定理が論理式を使った簡単な考察だけで証明できます。
【定理6】$A \subseteq X$ とすると、次が成立する。
i) $X$ がコンパクトのとき、$A$ が閉集合ならばコンパクトである。
ii) $X$ がハウスドルフのとき、$A$ がコンパクトならば閉集合である。
i) $X$ がコンパクトのとき、$A$ が閉集合ならばコンパクトである。
ii) $X$ がハウスドルフのとき、$A$ がコンパクトならば閉集合である。
(証明)
i) 任意に $y \in {}^*A$ をとる。$X$ がコンパクトだから【定理5】より $y \in \mathrm{monad}(x)$ となる $x \in X$ が存在する。$y \in \mathrm{monad}(x) \cap {}^*A$ すなわち $\mathrm{monad}(x) \cap {}^*A \neq \emptyset$ で、$A$ は閉集合だから、【定理3】ii) より $x \in A$ となる。従って $\forall y \in {}^*A \, \exists x \in A \, (y \in \mathrm{monad}(x))$ であるから、再び【定理5】より $A$ はコンパクトである。
ii) 任意に $\mathrm{monad}(x) \cap {}^*A \neq \emptyset$ をみたす $x \in X$ をとる。$y \in \mathrm{monad}(x) \cap {}^*A$ をとると、$A$ がコンパクトだから【定理5】より $y \in \mathrm{monad}(x')$ となる $x' \in A$ がある。$\mathrm{monad}(x) \cap \mathrm{monad}(x') \neq \emptyset$ で $X$ がハウスドルフだから、【定理4】ii) より $x = x'$ であり、これより $x \in A$ となる。従って【定理3】ii) より $A$ は閉集合である。
□
なお、$\exists x \in X \, (y \in \mathrm{monad}(x))$ をみたす $y \in {}^*X$ を ${}^*X$ の近標準点といい、そうでない $y \in {}^*X$ を ${}^*X$ の遠標準点といいます。この用語を使うと、空間 $X$ 自身がコンパクトであることは「すべての ${}^*X$ の点が近標準点である」ことと同値です。
[参考文献]
中村 徹『超準解析と物理学(増補改訂版)』(日本評論社, 2017)
(続く)(前記事)(目次)
吉野から熊野へ大峰山東側ルートをコミュニティバスで抜ける(その2) [バス]
(その1)へ戻る
【2日目】スポーツ公園宿舎前→七色→(徒歩)→神川温泉→熊野市→松阪→(大阪)鶴橋
腰の痛みは一晩寝てだいぶましになりました。
朝7時台の下北山村営バスで、県境を越えて和歌山県の飛地、北山村の七色に向かいます。
ゆうゆうバスはスポーツ公園の宿舎前まで来てくれないので、昨日は腰の痛みを堪えて少々歩きましたが、村営バスはすぐ前にバス停があるので楽です。


不動トンネルを抜けると和歌山県です。また少し山並みの雰囲気が変わった気がします。



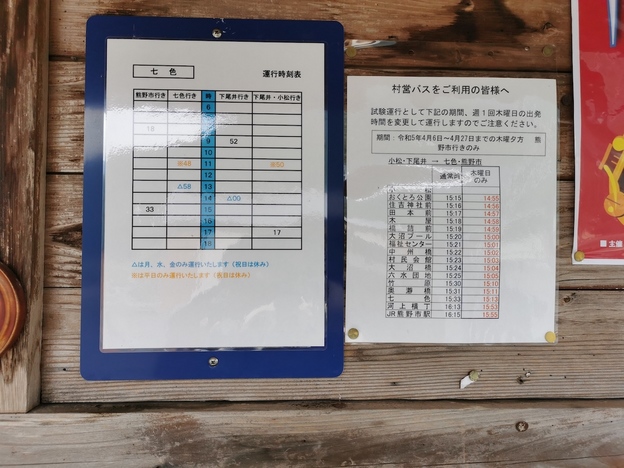
北山村の七色に着きました。ここで熊野市営バスや北山村営バスと乗り継ぐと熊野市駅方面に向かうことができます。


北山村営バスで北山村の中心地に向かうこともできますが、時間のロスが大きく帰りのバスの時刻がだいぶ遅くなりそうなのでそれは諦め、七色ダムの方向に少し散歩して1本後の熊野市営バスで熊野市駅に向かうことにしました。

国道169号を北山川に沿って歩きます。このあたりは「七色峡」という岩の多い峡谷になっています。



少し歩くと七色ダムに着きます。重力式アーチダムで、水力発電所があります。




七色ダムの堤を越えると三重県熊野市に入り、しばらく歩いて神川温泉のバス停から熊野市営バスに乗ります。今度は三重交通による運行のようです。



杉林を抜け分水嶺のトンネルを越えると、井戸川に沿って熊野市駅方面に降りて行きます。




イオンのある市街地が見えてくると、間も無く熊野市駅に到着です。



市役所前の食堂でちょっと豪華目の昼食をいただき、6月末で定期運行終了のキハ85系南紀で帰路につきました。


十津川村を通り抜ける奈良交通八木新宮線と並び立つ、もう一つの紀伊半島南北縦断ルートを路線バスで通り抜けることができ、課題をクリアした気分になりました。山深い渓谷や温泉も堪能できて旅行としても満足でした。
「路線バス歩き」のすすめ(目次)へ
【2日目】スポーツ公園宿舎前→七色→(徒歩)→神川温泉→熊野市→松阪→(大阪)鶴橋
腰の痛みは一晩寝てだいぶましになりました。
朝7時台の下北山村営バスで、県境を越えて和歌山県の飛地、北山村の七色に向かいます。
ゆうゆうバスはスポーツ公園の宿舎前まで来てくれないので、昨日は腰の痛みを堪えて少々歩きましたが、村営バスはすぐ前にバス停があるので楽です。


不動トンネルを抜けると和歌山県です。また少し山並みの雰囲気が変わった気がします。



北山村の七色に着きました。ここで熊野市営バスや北山村営バスと乗り継ぐと熊野市駅方面に向かうことができます。


北山村営バスで北山村の中心地に向かうこともできますが、時間のロスが大きく帰りのバスの時刻がだいぶ遅くなりそうなのでそれは諦め、七色ダムの方向に少し散歩して1本後の熊野市営バスで熊野市駅に向かうことにしました。


国道169号を北山川に沿って歩きます。このあたりは「七色峡」という岩の多い峡谷になっています。




少し歩くと七色ダムに着きます。重力式アーチダムで、水力発電所があります。




七色ダムの堤を越えると三重県熊野市に入り、しばらく歩いて神川温泉のバス停から熊野市営バスに乗ります。今度は三重交通による運行のようです。



杉林を抜け分水嶺のトンネルを越えると、井戸川に沿って熊野市駅方面に降りて行きます。




イオンのある市街地が見えてくると、間も無く熊野市駅に到着です。



市役所前の食堂でちょっと豪華目の昼食をいただき、6月末で定期運行終了のキハ85系南紀で帰路につきました。


十津川村を通り抜ける奈良交通八木新宮線と並び立つ、もう一つの紀伊半島南北縦断ルートを路線バスで通り抜けることができ、課題をクリアした気分になりました。山深い渓谷や温泉も堪能できて旅行としても満足でした。
「路線バス歩き」のすすめ(目次)へ
吉野から熊野へ大峰山東側ルートをコミュニティバスで抜ける(その1) [バス]
ずっと課題になっていた、吉野郡の大峰山の東側を国道169号に沿って70km以上走る「R169ゆうゆうバス」に、ようやく乗ることができ、これを使って吉野町の近鉄大和上市駅から熊野市駅まで通り抜けてきました。
このルートはかつて奈良交通の「北山峡特急バス」が走っていましたが、今は廃止されて、コミュニティバスの3路線の乗り継ぎになりました。徒歩区間なしで乗り継ぐことができますが、曜日に注意が必要です。大和上市駅から下北山村までは「R169ゆうゆうバス」という長距離のコミュニティバスがありますが、1日に1往復しかなく、平日は午前に北向きで午後に南向き、土休日は逆に午前に南向きで午後に北向きという変則的な運行です。そして下北山村から和歌山県北山村の七色に抜ける下北山村営バスは平日しか走りません。どのようにしても途中下北山村内での1泊が必要ですが、今回は日曜日から月曜日にかけての1泊2日とし、泊地の下北山村でゆっくり時間を取ることにしました。
【1日目】大阪阿部野橋→大和上市→下桑原→(徒歩)→寺垣内→池原大橋
早朝に大阪を出発し、大和上市駅で8:30発のゆうゆうバスに乗ります。運行は奈良交通です。



このバスの運賃は通常なら大和上市から終点の下桑原まで2900円ですが、事前に下北山村役場へ申込書を郵送して「地域公共交通パスポート」と「特別乗車証」を入手すると、1000円で乗車することができます(下北山村内での乗降が条件)。乗車証に乗降区間を記入し、後車時にパスポートを見せて乗車証と現金1000円を渡す方式です。

吉野川沿いに国道169号をひたすら南下して行きます。



川上村に入るとまもなく大滝ダムが見え、それを超えるとダム湖沿いの道になります。



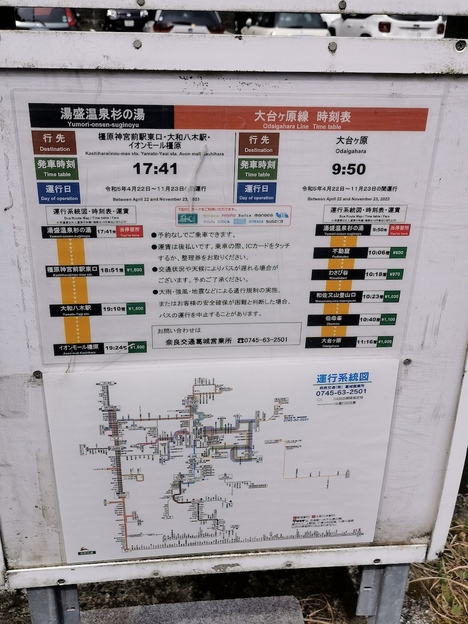
ほどなく「湯盛温泉杉の湯」に到着し、ここで20分トイレ休憩です。ホテルと道の駅があります。


大和上市駅からここまでは川上村営の「やまぶきバス」もあるのですが、土休日には運行しません。

他には春から秋にかけて、大和八木駅から大台ヶ原に行くバスがここを経由します。出発時にちょうど入れ替わりになるように遭遇しました。

吉野川に沿って坂道を登っていき、ループ橋を超えると、トンネルの手前で大台ヶ原ドライブウェイと分岐します。




分水嶺の新伯母峯トンネルを越えて上北山村に入ると、熊野灘に注ぐ北山川に沿って下って行きます。
両側の山が高く深い谷です。




大きなダム湖の池原貯水池沿いにしばらく走り、下北山村に入るとまもなく池原ダムが見えます。



最後は国道169号を離れて国道425号に入り、下北山村の中心地を通り抜けると、終点の下桑原です。
ここまで約2時間40分のロングラン乗車です。運転手さんもお疲れ様です。




周囲は商店は何もないですが、ちょっとした公園と公衆トイレがあるので助かります。大阪で買ってきたコンビニ弁当をここで食べました。
バスは川沿いの空き地で折り返しまで休憩です。


今夜の宿泊は温泉のある池原地区で、ここからはかなり距離があるので、役場のある寺垣内地区まで川沿いを歩き、そこからまた戻りのゆうゆうバスに乗って池原地区まで行くことにします。



橿原まで95km。同じ奈良県でも遠くまで来たものです。


郵便局や村役場のある寺垣内まで来ましたが、ここまで休憩できるカフェなどはなく、ひたすら川と山を眺めて歩くだけです。いつもはこれくらいの距離は平気なのですが、今回はどういうわけか4kmくらいから腰が痛くて歩くのが非常に辛くなってしまいました。バス停に椅子があったのが幸いです。



寺垣内から戻りのゆうゆうバスに乗って、池原大橋で下車し、少し歩いて宿泊地に行きます。




温泉で痛めた腰を温め、そこの食堂で鹿肉と豚肉の合い挽きハンバーグの定食を食べました。

(その2)へ続く
「路線バス歩き」のすすめ(目次)へ
このルートはかつて奈良交通の「北山峡特急バス」が走っていましたが、今は廃止されて、コミュニティバスの3路線の乗り継ぎになりました。徒歩区間なしで乗り継ぐことができますが、曜日に注意が必要です。大和上市駅から下北山村までは「R169ゆうゆうバス」という長距離のコミュニティバスがありますが、1日に1往復しかなく、平日は午前に北向きで午後に南向き、土休日は逆に午前に南向きで午後に北向きという変則的な運行です。そして下北山村から和歌山県北山村の七色に抜ける下北山村営バスは平日しか走りません。どのようにしても途中下北山村内での1泊が必要ですが、今回は日曜日から月曜日にかけての1泊2日とし、泊地の下北山村でゆっくり時間を取ることにしました。
【1日目】大阪阿部野橋→大和上市→下桑原→(徒歩)→寺垣内→池原大橋
早朝に大阪を出発し、大和上市駅で8:30発のゆうゆうバスに乗ります。運行は奈良交通です。



このバスの運賃は通常なら大和上市から終点の下桑原まで2900円ですが、事前に下北山村役場へ申込書を郵送して「地域公共交通パスポート」と「特別乗車証」を入手すると、1000円で乗車することができます(下北山村内での乗降が条件)。乗車証に乗降区間を記入し、後車時にパスポートを見せて乗車証と現金1000円を渡す方式です。

吉野川沿いに国道169号をひたすら南下して行きます。



川上村に入るとまもなく大滝ダムが見え、それを超えるとダム湖沿いの道になります。



ほどなく「湯盛温泉杉の湯」に到着し、ここで20分トイレ休憩です。ホテルと道の駅があります。


大和上市駅からここまでは川上村営の「やまぶきバス」もあるのですが、土休日には運行しません。

他には春から秋にかけて、大和八木駅から大台ヶ原に行くバスがここを経由します。出発時にちょうど入れ替わりになるように遭遇しました。


吉野川に沿って坂道を登っていき、ループ橋を超えると、トンネルの手前で大台ヶ原ドライブウェイと分岐します。




分水嶺の新伯母峯トンネルを越えて上北山村に入ると、熊野灘に注ぐ北山川に沿って下って行きます。
両側の山が高く深い谷です。




大きなダム湖の池原貯水池沿いにしばらく走り、下北山村に入るとまもなく池原ダムが見えます。



最後は国道169号を離れて国道425号に入り、下北山村の中心地を通り抜けると、終点の下桑原です。
ここまで約2時間40分のロングラン乗車です。運転手さんもお疲れ様です。




周囲は商店は何もないですが、ちょっとした公園と公衆トイレがあるので助かります。大阪で買ってきたコンビニ弁当をここで食べました。
バスは川沿いの空き地で折り返しまで休憩です。



今夜の宿泊は温泉のある池原地区で、ここからはかなり距離があるので、役場のある寺垣内地区まで川沿いを歩き、そこからまた戻りのゆうゆうバスに乗って池原地区まで行くことにします。



橿原まで95km。同じ奈良県でも遠くまで来たものです。


郵便局や村役場のある寺垣内まで来ましたが、ここまで休憩できるカフェなどはなく、ひたすら川と山を眺めて歩くだけです。いつもはこれくらいの距離は平気なのですが、今回はどういうわけか4kmくらいから腰が痛くて歩くのが非常に辛くなってしまいました。バス停に椅子があったのが幸いです。



寺垣内から戻りのゆうゆうバスに乗って、池原大橋で下車し、少し歩いて宿泊地に行きます。




温泉で痛めた腰を温め、そこの食堂で鹿肉と豚肉の合い挽きハンバーグの定食を食べました。

(その2)へ続く
「路線バス歩き」のすすめ(目次)へ



