天理〜上野市 今月限りの名阪国道バス乗り継ぎ [バス]
かつて、三重交通と奈良交通が共同で、名阪国道を経由する天理駅〜上野市駅の都市間バスを運行していました。この路線はその後、途中の針インターと国道山添で乗り継ぎとなる3路線に分割されましたが、両区間を路線バスだけで移動できるルートとして残ってきました。
しかし、この3月末で奈良交通が真ん中の針インター〜国道山添の路線を廃止することになり、4月からはバスでの乗り継ぎ移動が不可になってしまうので、名残の乗車をしてきました。
ルートはこちら。ついでに山添村コミュニティバスで山添村から名張駅までの乗車もしてきました。
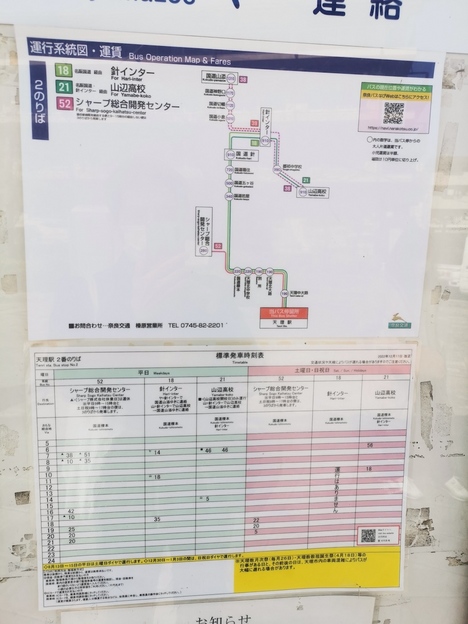
天理駅前の奈良交通路線図と時刻表。現時点でも針インター〜国道山添間は平日しか走りませんが、これが4月からは完全に廃止となります。
天理駅11:18発の針インター行に乗車します。新型コロナ対策でずっと座れなかった通称「あほ席」が解禁になっていました。


天理市内を少し走ってから、名阪国道に乗ります。


速度違反の車にバンバン抜かされながら、「Ωカーブ」を登坂車線でゆっくり走ります。名阪国道は高速道路ではないので、客席にシートベルトはありません。


本線上にある国道福住と国道針のバス停。まだこの区間のバス停はしばらく残ります。


ドライブイン施設のある針インターに到着しました。乗継時間が1分しかないので慌ただしいなと思ったら、なんとそのまま同じバスで国道山添行になり、乗換せずに先へ行くことができました(どの便もそうなのかは知りません)。


下道を少し走って山辺高校に立ち寄ります。ここまでは4月以降も残る路線です。
山辺高校はバスが他に3台待機していました。


ここからはいよいよ廃止される区間です。


奈良市(旧都祁村)から山添村に突入。途中のバス停も3月末限りです。



山添インターを降りて、終点の国道山添に到着です。



5分ほど遅れて到着したので次の三重交通バスへの乗継時間が3分しかなく、しかもバス停の場所が国道を挟んだ反対側にあるのでちょっと焦りました。僕はこの場所には数年前に一度来ていたので迷わずにすみましたが、初めての人は運転手さんに聞いておかないと混乱すると思います。

治田インターまでは下道「非名阪」を走り、その先は名阪国道です。


大内インター付近に1年前まであったドライブインは、すっかり更地になっていました。

12:58に上野市駅に到着しました。乗り継ぎが良いので所要時間は1時間40分、運賃は合計2,080円です。同じ区間を電車なら11:28出発で13:03に到着(近鉄+伊賀鉄道)で所要時間1時間35分、運賃は1,270円(4月からは近鉄の値上げで1,440円)なので、値段は割高ですが乗換が少なく楽という意味では悪くない交通機関だったと思います。

さて、上野公園で少々時間をつぶし、桑町までちょっとだけ伊賀鉄道に乗って……



また同じ三重交通バスで国道山添に戻ります。


さっき時間がなくて見れなかった、国道山添バス停の時刻表をじっくり見ることにします。
奈良交通の針インター行。これは標柱ごと無くなるのでしょう。



同じ場所にある三重交通の高速バス梅田・新大阪行は、2021年1月から運休中です。復活しないのでしょうか。

少し歩いて、山添村役場のある大西から、今度は山添村コミュニティバスに乗って名張駅に向かいます。これも平日だけの運行です。


運転席との間は透明シートが貼られていて、前面展望はダメでした。写真は全部左側の窓越しです。


カーブの多い峠を越えて、名張川沿いに走ります。



桔梗が丘の住宅地と、名張の旧市街地を抜けていきます。


名張駅前の広場に入るのかと思ったら、駅から3分ほど離れた駐車場まで連れて行かれました。




携帯の電池が尽きそうなので、コンセントのあるアーバンライナーに乗って帰ります。

天理駅〜上野市駅の名阪国道バスルートは、3月31日までの平日ならまだ乗車できます。名阪国道を一般路線バスでぶち抜くのも味わいありますので、乗りたくなった方はお急ぎください。
「路線バス歩き」のすすめ(目次)へ
しかし、この3月末で奈良交通が真ん中の針インター〜国道山添の路線を廃止することになり、4月からはバスでの乗り継ぎ移動が不可になってしまうので、名残の乗車をしてきました。
ルートはこちら。ついでに山添村コミュニティバスで山添村から名張駅までの乗車もしてきました。
天理駅前の奈良交通路線図と時刻表。現時点でも針インター〜国道山添間は平日しか走りませんが、これが4月からは完全に廃止となります。

天理駅11:18発の針インター行に乗車します。新型コロナ対策でずっと座れなかった通称「あほ席」が解禁になっていました。


天理市内を少し走ってから、名阪国道に乗ります。


速度違反の車にバンバン抜かされながら、「Ωカーブ」を登坂車線でゆっくり走ります。名阪国道は高速道路ではないので、客席にシートベルトはありません。


本線上にある国道福住と国道針のバス停。まだこの区間のバス停はしばらく残ります。


ドライブイン施設のある針インターに到着しました。乗継時間が1分しかないので慌ただしいなと思ったら、なんとそのまま同じバスで国道山添行になり、乗換せずに先へ行くことができました(どの便もそうなのかは知りません)。


下道を少し走って山辺高校に立ち寄ります。ここまでは4月以降も残る路線です。
山辺高校はバスが他に3台待機していました。


ここからはいよいよ廃止される区間です。


奈良市(旧都祁村)から山添村に突入。途中のバス停も3月末限りです。



山添インターを降りて、終点の国道山添に到着です。



5分ほど遅れて到着したので次の三重交通バスへの乗継時間が3分しかなく、しかもバス停の場所が国道を挟んだ反対側にあるのでちょっと焦りました。僕はこの場所には数年前に一度来ていたので迷わずにすみましたが、初めての人は運転手さんに聞いておかないと混乱すると思います。

治田インターまでは下道「非名阪」を走り、その先は名阪国道です。


大内インター付近に1年前まであったドライブインは、すっかり更地になっていました。

12:58に上野市駅に到着しました。乗り継ぎが良いので所要時間は1時間40分、運賃は合計2,080円です。同じ区間を電車なら11:28出発で13:03に到着(近鉄+伊賀鉄道)で所要時間1時間35分、運賃は1,270円(4月からは近鉄の値上げで1,440円)なので、値段は割高ですが乗換が少なく楽という意味では悪くない交通機関だったと思います。

さて、上野公園で少々時間をつぶし、桑町までちょっとだけ伊賀鉄道に乗って……



また同じ三重交通バスで国道山添に戻ります。


さっき時間がなくて見れなかった、国道山添バス停の時刻表をじっくり見ることにします。
奈良交通の針インター行。これは標柱ごと無くなるのでしょう。



同じ場所にある三重交通の高速バス梅田・新大阪行は、2021年1月から運休中です。復活しないのでしょうか。

少し歩いて、山添村役場のある大西から、今度は山添村コミュニティバスに乗って名張駅に向かいます。これも平日だけの運行です。


運転席との間は透明シートが貼られていて、前面展望はダメでした。写真は全部左側の窓越しです。


カーブの多い峠を越えて、名張川沿いに走ります。



桔梗が丘の住宅地と、名張の旧市街地を抜けていきます。


名張駅前の広場に入るのかと思ったら、駅から3分ほど離れた駐車場まで連れて行かれました。




携帯の電池が尽きそうなので、コンセントのあるアーバンライナーに乗って帰ります。

天理駅〜上野市駅の名阪国道バスルートは、3月31日までの平日ならまだ乗車できます。名阪国道を一般路線バスでぶち抜くのも味わいありますので、乗りたくなった方はお急ぎください。
「路線バス歩き」のすすめ(目次)へ
ウカシェビッチの公理系から全トートロジーが証明可能なことを証明する(勉強ノート) [数学]
命題論理において、最小限の公理系によって形式化された体系として、ポーランドのヤン・ウカシェビッチが考案した公理系が知られています。この体系を使うと、命題論理の全てのトートロジー(恒真式)が形式的に証明できます。面白そうだったので自分で実際にやってみましたが、あまり簡単ではなくパズルみたいな面白さがありましたので、本記事ではこれを一通り紹介します。
1. 論理式と形式的証明の定義
まず、本記事における論理式を次で定義します。
以下、論理式の記述において、カッコは紛れがない限り省略し、論理演算子 $\lnot, \to$ の結合は $\lnot$ が $\to$ より強いものとします。例えば $\lnot A \to B$ は正式には $(\lnot (A)) \to (B)$ のことです。
一般の論理体系では他に $\lor, \land, \leftrightarrow$ といった論理演算子も使われますが、本記事ではこれらは略記法とみなします。つまり、
i) $A \lor B$ は $\lnot A \to B$ の略記
ii) $A \land B$ は $\lnot(A \to \lnot B)$ の略記
iii) $A \leftrightarrow B$ は $(A \to B) \land (B \to A)$ の略記
とします。本記事では最後までこれらの論理演算子は使わず、$\lnot$ と $\to$ だけで突っ走ります。
次に、論理の公理を定義します。ウカシェビッチの公理系といわれるものです。
これらを使って、次によって形式的証明が定義されます。
この定義の iii) で、「$B_j$ と $B_j \to B_i$ から $B_i$ を推論すること」が形式的証明における推論規則として定められています。この推論規則をモーダス・ポーネンスといい、以下「MP」と略記します。本記事で使う推論規則はMPだけです。
このように定義した形式的証明と、体系を外から取り扱う(メタ理論としての)証明は、ごっちゃになると紛らわしいので本記事では言葉を使い分けます。
2. いろいろな論理の定理の形式的証明
この体系でいろいろな論理式が論理の定理であることの形式的証明が得られます。公理の種類が少ないだけにその形式的証明はいささかトリッキーです。
まず最初に、一見あたりまえのような次の論理式を形式的に証明します。
(証明)
次は $A \to A$ の形式的証明である。各行の頭の (a),(b),…は識別記号であり、: の右側の記述は形式的証明に使われた根拠を表す。
□
このように、形式的証明をまじめにやると意外と手間がかかります。そこで、少しでも手間を省く強力な手法である演繹定理を先に証明します。
(証明)
$(2)$から$(1)$はMPより明らかなので、$(1)$から$(2)$を証明する。$(1)$より $\Sigma \cup \{A\}$ から $B$ への形式的証明となる論理式の列 $C_1, C_2, \cdots, C_{n-1}, B$ がある。形式的証明の長さ $n$ に関する帰納法を用いる。すなわち、$C_i \ (i < n)$ については全て $\Sigma \vdash A \to C_i$ であると仮定する。形式的証明の定義から $B$ について場合分けする。
i) $B$ が $\Sigma$ の要素(前提)、または論理の公理[A1] $\sim$ [A3]のいずれかのとき:
次は $\Sigma$ からの $A \to B$ の形式的証明である。
ii) $B$ が $A$ のとき:
[T1] が論理の定理だから $\vdash A \to A$ すなわち $\vdash A \to B$ である。
iii) $B$ がある $C_i, C_j \ (i,j < n)$ からMPによって得られるとき、すなわち $C_j$ が $C_i \to B$ のとき:
帰納法の仮定より $\Sigma \vdash A \to C_i$ かつ $\Sigma \vdash A \to (C_i \to B)$ である。従ってこれらの形式的証明となる論理式の列を連結し、それに次の論理式の列を追加することにより、$\Sigma$ からの $A \to B$ の形式的証明が得られる。
以上より全ての場合について$(2)$が示された。
□
演繹定理を利用すると、以下次々と論理の定理が形式的に証明できます。
(証明)
[T2] 演繹定理より $\{ \lnot A \} \vdash A \to B$ を示せばよい。
[T3] $\{ \lnot \lnot A \} \vdash A$ を示せばよい。
[T4]
[T5] $\{ A \to (B \to C), B, A \} \vdash C$ を示せばよい。
[T6] $\{ A \to B, B \to C, A \} \vdash C$ を示せばよい。
[T7] $\{ \lnot A \to A \} \vdash A$ を示せばよい。
[T8] $\{ A \to B, \lnot A \to B \} \vdash B$ を示せばよい。
[T9] $\{ A \to B \} \vdash \lnot B \to \lnot A$ を示せばよい。
[T10] $\{ A \} \vdash \lnot B \to \lnot(A \to B)$ を示せばよい。
□
このようにして、論理の定理がいくらでも形式的に証明できますが、キリがないのでここでやめておきます。
3. トートロジーが形式的証明可能なことの証明
ここまでの議論では、論理演算子 $\lnot, \to$ や推論規則には何の意味もなく、形式的証明はただ記号列を規則に従って並べているだけでした。これから論理演算子に意味を持たせ、論理式の真偽を定義します。
トートロジーを言い換えると、原始命題の真理値をどのように割り当てても真になる論理式ということです。定義から具体的に検証することによって、論理の公理 [A1] $\sim$ [A3] は全てトートロジーになることが分かります。
このように論理式に真偽の意味を持たせると、形式的証明が次の定理によって意味づけされます。
(証明)
$\Sigma \vdash A$ かつ $\Sigma$ の要素が全て真とする。$\Sigma$ から $A$ への形式的証明を $B_1, B_2, \cdots, B_{n-1}, A$ とし、$i < n$ に対して定理が成り立つ、すなわち $\Sigma \models B_i \ (i < n)$ であると仮定すると、$B_i \ (i < n)$ は全て真である。
i) $A$ が $\Sigma$ の要素のとき:
明らかに $A$ は真である。
ii) $A$ が [A1] $\sim$ [A3] のいずれかのとき:
[A1] $\sim$ [A3] はどれもトートロジーだから、やはり $A$ は真 である。
iii) ある $B_i, B_j \ (i,j < n)$ に対して $B_j$ が $B_i \to A$ のとき:
$B_i$ が真、かつ $B_i \to A$ が真 であるから、【定義7】iii) より $A$ は真でなければならない。
以上より全ての場合で $A$ が真であるから、形式的証明の長さ $n$ に関する帰納法によって $\Sigma \models A$ が示された。
□
つまり「形式的に証明できれば論理的に正しい」と言って良いわけです。これによって、論理の定理は前提なしで形式的に証明できるので、全てトートロジーです。
逆に、トートロジーが全て形式的に証明できること、すなわち論理の定理であることの証明に進みます。準備として、論理式の真理値と形式的証明の関係がよくわかる次の補題を証明します。
(証明)
論理式 $A$ の構成に関する帰納法を用いる。
i) $A$ が原始命題 $P$ のとき:
(a) $P$ が真のとき $A$ は真である。このとき $\{ P \} \vdash P$ は自明だから $\{ P \} \vdash A$ となり、$(3)$が成立する。
(b) $P$ が偽のとき $A$ は偽である。このとき $\{ \lnot P \} \vdash \lnot P$ は自明だから $\{ \lnot P \} \vdash \lnot A$ となり、$(4)$が成立する。
ii) $A$ が $\lnot B$ で、$B$ について補題が成立するとき:
(a) $P_1, \cdots , P_m$ が真、$P_{m+1}, \cdots , P_n$ が偽のときに $A$ が真ならば、このとき $B$ は偽であるから、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash \lnot B
\end{equation*}
である。$\lnot B$ は $A$ だから$(3)$が成立する。
(b) $P_1, \cdots , P_m$ が真、$P_{m+1}, \cdots , P_n$ が偽のときに $A$ が偽ならば、このとき $B$ は真であるから、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash B
\end{equation*}
であり、さらに [T4] より $\vdash B \to \lnot \lnot B$ だから、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash \lnot \lnot B
\end{equation*}
である。$\lnot B$ は $A$ だから$(4)$が成立する。
iii) $A$ が $B \to C$ で、$B$ と $C$ について補題が成立するとき:
(a) $P_1, \cdots , P_m$ が真、$P_{m+1}, \cdots , P_n$ が偽のときに $A$ が真ならば、このとき $B$ が偽であるか、または $C$ が真である。
$B$ が偽の場合は、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash \lnot B
\end{equation*}
であり、さらに [T2] より $\vdash \lnot B \to (B \to C)$ だから、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash B \to C
\end{equation*}
である。$B \to C$ は $A$ だから$(3)$が成立する。
$C$ が真の場合は、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash C
\end{equation*}
であり、さらに [A1] より $\vdash C \to (B \to C)$ だから、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash B \to C
\end{equation*}
である。$B \to C$ は $A$ だから$(3)$が成立する。
(b) $P_1, \cdots , P_m$ が真、$P_{m+1}, \cdots , P_n$ が偽のときに $A$ が偽ならば、このとき $B$ が真かつ $C$ が偽であるから、
\begin{eqnarray*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} &\vdash& B \\
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} &\vdash& \lnot C
\end{eqnarray*}
であり、さらに [T10] より $\vdash B \to (\lnot C \to \lnot (B \to C))$ だから、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash \lnot (B \to C)
\end{equation*}
である。$B \to C$ は $A$ だから$(4)$が成立する。
以上より、全ての論理式 $A$ に対して補題が証明できた。
□
この補題を使って、本記事の目的である次の定理を証明します。
(証明)
$\models A$ とする。$A$ を構成する原始命題を全て取り出し $P_1, P_2, \cdots , P_n$ とすると、これらの真理値がどのように割り当てられても $A$ は真である。特に $P_n$ に注目すると、【補題10】より、
\begin{eqnarray*}
\{ P_1, \cdots , P_{n-1}, P_n \} &\vdash& A \\
\{ P_1, \cdots , P_{n-1}, \lnot P_n \} &\vdash& A
\end{eqnarray*}
である。これから演繹定理より、
\begin{eqnarray*}
\{ P_1, \cdots , P_{n-1} \} &\vdash& P_n \to A \\
\{ P_1, \cdots , P_{n-1} \} &\vdash& \lnot P_n \to A
\end{eqnarray*}
となる。一方 [T8] より、
\begin{equation*}
\vdash (P_n \to A) \to ((\lnot P_n \to A) \to A)
\end{equation*}
であるから、
\begin{equation*}
\{ P_1, \cdots , P_{n-2}, P_{n-1} \} \vdash A
\end{equation*}
が得られる。同様に、
\begin{eqnarray*}
\{ P_1, \cdots , P_{n-2}, \lnot P_{n-1}, P_n \} &\vdash& A \\
\{ P_1, \cdots , P_{n-2}, \lnot P_{n-1}, \lnot P_n \} &\vdash& A
\end{eqnarray*}
から
\begin{equation*}
\{ P_1, \cdots , P_{n-2}, \lnot P_{n-1} \} \vdash A
\end{equation*}
が得られる。従って、
\begin{eqnarray*}
\{ P_1, \cdots , P_{n-2}, P_{n-1} \} \vdash A \\
\{ P_1, \cdots , P_{n-2}, \lnot P_{n-1} \} \vdash A
\end{eqnarray*}
である。以下この操作を次々繰り返すと、最終的に
\begin{equation*}
\vdash A
\end{equation*}
が得られる。
□
たった3種類の公理系と1つの推論規則から全てのトートロジーが形式的に証明できることが、これで確認できました。
1. 論理式と形式的証明の定義
まず、本記事における論理式を次で定義します。
【定義1】(論理式)記号の集合として、原始命題と呼ばれる無限個の記号 $P_1 \ P_2 \ \cdots$ と、論理演算子と呼ばれる2個の記号 $\lnot \ \to$ およびカッコ $( \ )$ がある。このとき、次によって帰納的に定まる記号の列を論理式と呼ぶ。
i) 原始命題 $P_1, P_2, \cdots$ はそれぞれ論理式である。
ii) $A$ が論理式ならば $\lnot (A)$ は論理式である。
iii) $A, B$ が論理式ならば $(A) \to (B)$ は論理式である。
iv) 以上で定義されるものだけが論理式である。
i) 原始命題 $P_1, P_2, \cdots$ はそれぞれ論理式である。
ii) $A$ が論理式ならば $\lnot (A)$ は論理式である。
iii) $A, B$ が論理式ならば $(A) \to (B)$ は論理式である。
iv) 以上で定義されるものだけが論理式である。
以下、論理式の記述において、カッコは紛れがない限り省略し、論理演算子 $\lnot, \to$ の結合は $\lnot$ が $\to$ より強いものとします。例えば $\lnot A \to B$ は正式には $(\lnot (A)) \to (B)$ のことです。
一般の論理体系では他に $\lor, \land, \leftrightarrow$ といった論理演算子も使われますが、本記事ではこれらは略記法とみなします。つまり、
i) $A \lor B$ は $\lnot A \to B$ の略記
ii) $A \land B$ は $\lnot(A \to \lnot B)$ の略記
iii) $A \leftrightarrow B$ は $(A \to B) \land (B \to A)$ の略記
とします。本記事では最後までこれらの論理演算子は使わず、$\lnot$ と $\to$ だけで突っ走ります。
次に、論理の公理を定義します。ウカシェビッチの公理系といわれるものです。
【定義2】(論理の公理)$A,B,C$ が任意の論理式のとき、次の3種類の論理式を論理の公理という。
[A1] $A \to (B \to A)$
[A2] $(A \to (B \to C)) \to ((A \to B) \to (A \to C))$
[A3] $(\lnot B \to \lnot A) \to (A \to B)$
[A1] $A \to (B \to A)$
[A2] $(A \to (B \to C)) \to ((A \to B) \to (A \to C))$
[A3] $(\lnot B \to \lnot A) \to (A \to B)$
これらを使って、次によって形式的証明が定義されます。
【定義3】(形式的証明)$\Sigma$を論理式の集合、$A$ を論理式とする。論理式の有限個の列 $B_1, B_2, \cdots, B_{n-1}, B_n$ があり、$B_n$ が $A$ であって、かつ各々の $B_i$ が、
i) $\Sigma$ の要素である。
ii) 論理の公理 [A1] $\sim$ [A3] のいずれかである。
iii) ある $B_j, B_k \ (j,k < i)$ があって、$B_k$ が $B_j \to B_i$ となっている。
のいずれかをみたすとき、$A$ は $\Sigma$ から形式的証明可能といい、 \begin{equation*} \Sigma \vdash A \end{equation*} と書く。このとき、論理式の列 $B_1, B_2, \cdots, B_{n-1}, A$ を 「$\Sigma$ からの $A$ の形式的証明」といい、$\Sigma$ の要素となる論理式を前提、$A$ を結論という。
$\Sigma$ が空集合のとき、$\Sigma \vdash A$ を $\vdash A$ と書き、このとき $A$ を論理の定理という。
i) $\Sigma$ の要素である。
ii) 論理の公理 [A1] $\sim$ [A3] のいずれかである。
iii) ある $B_j, B_k \ (j,k < i)$ があって、$B_k$ が $B_j \to B_i$ となっている。
のいずれかをみたすとき、$A$ は $\Sigma$ から形式的証明可能といい、 \begin{equation*} \Sigma \vdash A \end{equation*} と書く。このとき、論理式の列 $B_1, B_2, \cdots, B_{n-1}, A$ を 「$\Sigma$ からの $A$ の形式的証明」といい、$\Sigma$ の要素となる論理式を前提、$A$ を結論という。
$\Sigma$ が空集合のとき、$\Sigma \vdash A$ を $\vdash A$ と書き、このとき $A$ を論理の定理という。
この定義の iii) で、「$B_j$ と $B_j \to B_i$ から $B_i$ を推論すること」が形式的証明における推論規則として定められています。この推論規則をモーダス・ポーネンスといい、以下「MP」と略記します。本記事で使う推論規則はMPだけです。
このように定義した形式的証明と、体系を外から取り扱う(メタ理論としての)証明は、ごっちゃになると紛らわしいので本記事では言葉を使い分けます。
2. いろいろな論理の定理の形式的証明
この体系でいろいろな論理式が論理の定理であることの形式的証明が得られます。公理の種類が少ないだけにその形式的証明はいささかトリッキーです。
まず最初に、一見あたりまえのような次の論理式を形式的に証明します。
【定理4】$A$ を任意の論理式とする。次の論理式は論理の定理である。
[T1] $A \to A$
[T1] $A \to A$
(証明)
次は $A \to A$ の形式的証明である。各行の頭の (a),(b),…は識別記号であり、: の右側の記述は形式的証明に使われた根拠を表す。
| (a) | $A \to ((A \to A) \to A)$ | : [A1] |
| (b) | $(A \to ((A \to A) \to A)) \to ((A \to (A \to A)) \to (A \to A))$ | : [A2] |
| (c) | $(A \to (A \to A)) \to (A \to A)$ | : (a),(b),MP |
| (d) | $A \to (A \to A)$ | : [A1] |
| (e) | $A \to A$ | : (d),(c),MP |
□
このように、形式的証明をまじめにやると意外と手間がかかります。そこで、少しでも手間を省く強力な手法である演繹定理を先に証明します。
【定理5】(演繹定理)$\Sigma$を論理式の集合、$A, B$ を論理式とするとき、
\begin{equation} \tag{1}
\Sigma \cup \{A\} \vdash B
\end{equation}
であることと、
\begin{equation} \tag{2}
\Sigma \vdash A \to B
\end{equation}
であることとは同値である。
(証明)
$(2)$から$(1)$はMPより明らかなので、$(1)$から$(2)$を証明する。$(1)$より $\Sigma \cup \{A\}$ から $B$ への形式的証明となる論理式の列 $C_1, C_2, \cdots, C_{n-1}, B$ がある。形式的証明の長さ $n$ に関する帰納法を用いる。すなわち、$C_i \ (i < n)$ については全て $\Sigma \vdash A \to C_i$ であると仮定する。形式的証明の定義から $B$ について場合分けする。
i) $B$ が $\Sigma$ の要素(前提)、または論理の公理[A1] $\sim$ [A3]のいずれかのとき:
次は $\Sigma$ からの $A \to B$ の形式的証明である。
| (a) | $B$ | : 前提または論理の公理 |
| (b) | $B \to (A \to B)$ | : [A1] |
| (c) | $A \to B$ | : (a),(b),MP |
ii) $B$ が $A$ のとき:
[T1] が論理の定理だから $\vdash A \to A$ すなわち $\vdash A \to B$ である。
iii) $B$ がある $C_i, C_j \ (i,j < n)$ からMPによって得られるとき、すなわち $C_j$ が $C_i \to B$ のとき:
帰納法の仮定より $\Sigma \vdash A \to C_i$ かつ $\Sigma \vdash A \to (C_i \to B)$ である。従ってこれらの形式的証明となる論理式の列を連結し、それに次の論理式の列を追加することにより、$\Sigma$ からの $A \to B$ の形式的証明が得られる。
| (a) | $(A \to (C_i \to B)) \to ((A \to C_i) \to (A \to B))$ | : [A2] |
| (b) | $(A \to C_i) \to (A \to B)$ | : $A \to (C_i \to B)$, (a), MP |
| (c) | $A \to B$ | : $A \to C_i$, (b), MP |
以上より全ての場合について$(2)$が示された。
□
演繹定理を利用すると、以下次々と論理の定理が形式的に証明できます。
【定理6】$A,B,C$ を任意の論理式とする。次の各々は論理の定理である。
[T2] $\lnot A \to (A \to B)$
[T3] $\lnot \lnot A \to A$
[T4] $A \to \lnot \lnot A$
[T5] $(A \to (B \to C)) \to (B \to (A \to C))$
[T6] $(A \to B) \to ((B \to C) \to (A \to C))$
[T7] $(\lnot A \to A) \to A$
[T8] $(A \to B) \to ((\lnot A \to B) \to B)$
[T9] $(A \to B) \to (\lnot B \to \lnot A)$
[T10] $A \to (\lnot B \to \lnot(A \to B))$
[T2] $\lnot A \to (A \to B)$
[T3] $\lnot \lnot A \to A$
[T4] $A \to \lnot \lnot A$
[T5] $(A \to (B \to C)) \to (B \to (A \to C))$
[T6] $(A \to B) \to ((B \to C) \to (A \to C))$
[T7] $(\lnot A \to A) \to A$
[T8] $(A \to B) \to ((\lnot A \to B) \to B)$
[T9] $(A \to B) \to (\lnot B \to \lnot A)$
[T10] $A \to (\lnot B \to \lnot(A \to B))$
(証明)
[T2] 演繹定理より $\{ \lnot A \} \vdash A \to B$ を示せばよい。
| (a) | $\lnot A$ | : 前提 |
| (b) | $\lnot A \to (\lnot B \to \lnot A)$ | : [A1] |
| (c) | $\lnot B \to \lnot A$ | : (a),(b),MP |
| (d) | $(\lnot B \to \lnot A) \to (A \to B)$ | : [A3] |
| (e) | $A \to B$ | : (c),(d),MP |
[T3] $\{ \lnot \lnot A \} \vdash A$ を示せばよい。
| (a) | $\lnot \lnot A$ | : 前提 |
| (b) | $\lnot \lnot A \to (\lnot A \to \lnot \lnot \lnot A)$ | : [T2] |
| (c) | $\lnot A \to \lnot \lnot \lnot A$ | : (a),(b),MP |
| (d) | $(\lnot A \to \lnot \lnot \lnot A) \to (\lnot \lnot A \to A)$ | : [A3] |
| (e) | $\lnot \lnot A \to A$ | : (c),(d),MP |
| (f) | $A$ | : (a),(e),MP |
[T4]
| (a) | $\lnot \lnot \lnot A \to \lnot A$ | : [T3] |
| (b) | $(\lnot \lnot \lnot A \to \lnot A) \to (A \to \lnot \lnot A)$ | : [A3] |
| (c) | $A \to \lnot \lnot A$ | : (a),(b),MP |
[T5] $\{ A \to (B \to C), B, A \} \vdash C$ を示せばよい。
| (a) | $A$ | : 前提 |
| (b) | $A \to (B \to C)$ | : 前提 |
| (c) | $B \to C$ | : (a),(b),MP |
| (d) | $B$ | : 前提 |
| (e) | $C$ | : (d),(c),MP |
[T6] $\{ A \to B, B \to C, A \} \vdash C$ を示せばよい。
| (a) | $A$ | : 前提 |
| (b) | $A \to B$ | : 前提 |
| (c) | $B$ | : (a),(b),MP |
| (d) | $B \to C$ | : 前提 |
| (e) | $C$ | : (c),(d),MP |
[T7] $\{ \lnot A \to A \} \vdash A$ を示せばよい。
| (a) | $\lnot A \to (A \to \lnot (A \to A))$ | : [T2] |
| (b) | $(\lnot A \to (A \to \lnot (A \to A))) \to ((\lnot A \to A) \to (\lnot A \to \lnot (A \to A)))$ | : [A2] |
| (c) | $(\lnot A \to A) \to (\lnot A \to \lnot (A \to A))$ | : (a),(b),MP |
| (d) | $\lnot A \to A$ | : 前提 |
| (e) | $\lnot A \to \lnot (A \to A)$ | : (d),(c),MP |
| (f) | $(\lnot A \to \lnot (A \to A)) \to ((A \to A) \to A)$ | : [A3] |
| (g) | $(A \to A) \to A$ | : (e),(f),MP |
| (h) | $A \to A$ | : [T1] |
| (i) | $A$ | : (h),(g),MP |
[T8] $\{ A \to B, \lnot A \to B \} \vdash B$ を示せばよい。
| (a) | $\lnot A \to B$ | : 前提 |
| (b) | $(\lnot A \to B) \to ((B \to \lnot \lnot B) \to (\lnot A \to \lnot \lnot B))$ | : [T6] |
| (c) | $(B \to \lnot \lnot B) \to (\lnot A \to \lnot \lnot B)$ | : (a),(b),MP |
| (d) | $B \to \lnot \lnot B$ | : [T4] |
| (e) | $\lnot A \to \lnot \lnot B$ | : (d),(c),MP |
| (f) | $(\lnot A \to \lnot \lnot B) \to (\lnot B \to A)$ | : [A3] |
| (g) | $\lnot B \to A$ | : (e),(f),MP |
| (h) | $(\lnot B \to A) \to ((A \to B) \to (\lnot B \to B))$ | : [T6] |
| (i) | $(A \to B) \to (\lnot B \to B)$ | : (g),(h),MP |
| (j) | $A \to B$ | : 前提 |
| (k) | $\lnot B \to B$ | : (j),(i),MP |
| (l) | $(\lnot B \to B) \to B$ | : [T7] |
| (m) | $B$ | : (k),(l),MP |
[T9] $\{ A \to B \} \vdash \lnot B \to \lnot A$ を示せばよい。
| (a) | $A \to B$ | : 前提 |
| (b) | $(A \to B) \to ((B \to \lnot \lnot B) \to (A \to \lnot \lnot B))$ | : [T6] |
| (c) | $(B \to \lnot \lnot B) \to (A \to \lnot \lnot B)$ | : (a),(b),MP |
| (d) | $B \to \lnot \lnot B$ | : [T4] |
| (e) | $A \to \lnot \lnot B$ | : (d),(c),MP |
| (f) | $\lnot \lnot A \to A$ | : [T3] |
| (g) | $(\lnot \lnot A \to A) \to ((A \to \lnot \lnot B) \to (\lnot \lnot A \to \lnot \lnot B))$ | : [T6] |
| (h) | $(A \to \lnot \lnot B) \to (\lnot \lnot A \to \lnot \lnot B)$ | : (f),(g),MP |
| (i) | $\lnot \lnot A \to \lnot \lnot B$ | : (e),(h),MP |
| (j) | $(\lnot \lnot A \to \lnot \lnot B) \to (\lnot B \to \lnot A)$ | : [A3] |
| (k) | $\lnot B \to \lnot A$ | : (i),(j),MP |
[T10] $\{ A \} \vdash \lnot B \to \lnot(A \to B)$ を示せばよい。
| (a) | $(A \to B) \to (A \to B)$ | : [T1] |
| (b) | $((A \to B) \to (A \to B)) \to (A \to ((A \to B) \to B))$ | : [T5] |
| (c) | $A \to ((A \to B) \to B)$ | : (a),(b),MP |
| (d) | $A$ | : 前提 |
| (e) | $(A \to B) \to B$ | : (d),(c),MP |
| (f) | $((A \to B) \to B) \to (\lnot B \to \lnot(A \to B))$ | : [T9] |
| (g) | $\lnot B \to \lnot(A \to B)$ | : (e),(f),MP |
□
このようにして、論理の定理がいくらでも形式的に証明できますが、キリがないのでここでやめておきます。
3. トートロジーが形式的証明可能なことの証明
ここまでの議論では、論理演算子 $\lnot, \to$ や推論規則には何の意味もなく、形式的証明はただ記号列を規則に従って並べているだけでした。これから論理演算子に意味を持たせ、論理式の真偽を定義します。
【定義7】(論理式の真偽)議論の対象としている原始命題それぞれに真理値と呼ばれる $\{$ 真, 偽 $\}$ どちらかの値が割り当てられているとする。このとき、論理式 $A$ の真理値を次で帰納的に与える。
i) $A$ が原始命題 $P$ のとき:
・$A$ の真理値は $P$ の真理値と同じ
ii) $A$ が $\lnot B$ で $B$ が論理式のとき:
・$B$ の真理値が真ならば $A$ の真理値は偽
・$B$ の真理値が偽ならば $A$ の真理値は真
(これは論理演算子 $\lnot$ に否定の意味を持たせることである。)
iii) $A$ が $B \to C$ で $B, C$ が論理式のとき:
・$B$ の真理値が真かつ $C$ の真理値が偽ならば $A$ の真理値は偽
・それ以外の場合は $A$ の真理値は真
(これは論理演算子 $\to$ に「ならば」の意味を持たせることである。)
論理式 $A$ の真理値が真のとき「$A$ は真」、真理値が偽のとき「$A$ は偽」という。
i) $A$ が原始命題 $P$ のとき:
・$A$ の真理値は $P$ の真理値と同じ
ii) $A$ が $\lnot B$ で $B$ が論理式のとき:
・$B$ の真理値が真ならば $A$ の真理値は偽
・$B$ の真理値が偽ならば $A$ の真理値は真
(これは論理演算子 $\lnot$ に否定の意味を持たせることである。)
iii) $A$ が $B \to C$ で $B, C$ が論理式のとき:
・$B$ の真理値が真かつ $C$ の真理値が偽ならば $A$ の真理値は偽
・それ以外の場合は $A$ の真理値は真
(これは論理演算子 $\to$ に「ならば」の意味を持たせることである。)
論理式 $A$ の真理値が真のとき「$A$ は真」、真理値が偽のとき「$A$ は偽」という。
【定義8】(論理的帰結)$\Sigma$ に属する論理式が全て真ならば論理式 $A$ が必ず真になるとき、$A$ は $\Sigma$ の論理的帰結であるといい、
\begin{equation*}
\Sigma \models A
\end{equation*}
と書く。$\Sigma$ が空集合のときは
\begin{equation*}
\models A
\end{equation*}
と書き、$A$ はトートロジー(恒真式)であるという。
トートロジーを言い換えると、原始命題の真理値をどのように割り当てても真になる論理式ということです。定義から具体的に検証することによって、論理の公理 [A1] $\sim$ [A3] は全てトートロジーになることが分かります。
このように論理式に真偽の意味を持たせると、形式的証明が次の定理によって意味づけされます。
【定理9】(健全性定理)$\Sigma \vdash A$ ならば $\Sigma \models A$ である。すなわち、$\Sigma$ から $A$ が形式的に証明できれば、$A$ は $\Sigma$ の論理的帰結である。
(証明)
$\Sigma \vdash A$ かつ $\Sigma$ の要素が全て真とする。$\Sigma$ から $A$ への形式的証明を $B_1, B_2, \cdots, B_{n-1}, A$ とし、$i < n$ に対して定理が成り立つ、すなわち $\Sigma \models B_i \ (i < n)$ であると仮定すると、$B_i \ (i < n)$ は全て真である。
i) $A$ が $\Sigma$ の要素のとき:
明らかに $A$ は真である。
ii) $A$ が [A1] $\sim$ [A3] のいずれかのとき:
[A1] $\sim$ [A3] はどれもトートロジーだから、やはり $A$ は真 である。
iii) ある $B_i, B_j \ (i,j < n)$ に対して $B_j$ が $B_i \to A$ のとき:
$B_i$ が真、かつ $B_i \to A$ が真 であるから、【定義7】iii) より $A$ は真でなければならない。
以上より全ての場合で $A$ が真であるから、形式的証明の長さ $n$ に関する帰納法によって $\Sigma \models A$ が示された。
□
つまり「形式的に証明できれば論理的に正しい」と言って良いわけです。これによって、論理の定理は前提なしで形式的に証明できるので、全てトートロジーです。
逆に、トートロジーが全て形式的に証明できること、すなわち論理の定理であることの証明に進みます。準備として、論理式の真理値と形式的証明の関係がよくわかる次の補題を証明します。
【補題10】論理式 $A$ を構成する原始命題は $P_1, P_2, \cdots , P_n$ 以外にないとする。$0 \le m \le n$ として、
(a) $P_1, \cdots , P_m$ が真、$P_{m+1}, \cdots , P_n$ が偽のときに $A$ が真ならば、 \begin{equation} \tag{3} \{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash A \end{equation} (b) $P_1, \cdots , P_m$ が真、$P_{m+1}, \cdots , P_n$ が偽のときに $A$ が偽ならば、 \begin{equation} \tag{4} \{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash \lnot A \end{equation}
(a) $P_1, \cdots , P_m$ が真、$P_{m+1}, \cdots , P_n$ が偽のときに $A$ が真ならば、 \begin{equation} \tag{3} \{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash A \end{equation} (b) $P_1, \cdots , P_m$ が真、$P_{m+1}, \cdots , P_n$ が偽のときに $A$ が偽ならば、 \begin{equation} \tag{4} \{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash \lnot A \end{equation}
(証明)
論理式 $A$ の構成に関する帰納法を用いる。
i) $A$ が原始命題 $P$ のとき:
(a) $P$ が真のとき $A$ は真である。このとき $\{ P \} \vdash P$ は自明だから $\{ P \} \vdash A$ となり、$(3)$が成立する。
(b) $P$ が偽のとき $A$ は偽である。このとき $\{ \lnot P \} \vdash \lnot P$ は自明だから $\{ \lnot P \} \vdash \lnot A$ となり、$(4)$が成立する。
ii) $A$ が $\lnot B$ で、$B$ について補題が成立するとき:
(a) $P_1, \cdots , P_m$ が真、$P_{m+1}, \cdots , P_n$ が偽のときに $A$ が真ならば、このとき $B$ は偽であるから、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash \lnot B
\end{equation*}
である。$\lnot B$ は $A$ だから$(3)$が成立する。
(b) $P_1, \cdots , P_m$ が真、$P_{m+1}, \cdots , P_n$ が偽のときに $A$ が偽ならば、このとき $B$ は真であるから、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash B
\end{equation*}
であり、さらに [T4] より $\vdash B \to \lnot \lnot B$ だから、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash \lnot \lnot B
\end{equation*}
である。$\lnot B$ は $A$ だから$(4)$が成立する。
iii) $A$ が $B \to C$ で、$B$ と $C$ について補題が成立するとき:
(a) $P_1, \cdots , P_m$ が真、$P_{m+1}, \cdots , P_n$ が偽のときに $A$ が真ならば、このとき $B$ が偽であるか、または $C$ が真である。
$B$ が偽の場合は、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash \lnot B
\end{equation*}
であり、さらに [T2] より $\vdash \lnot B \to (B \to C)$ だから、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash B \to C
\end{equation*}
である。$B \to C$ は $A$ だから$(3)$が成立する。
$C$ が真の場合は、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash C
\end{equation*}
であり、さらに [A1] より $\vdash C \to (B \to C)$ だから、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash B \to C
\end{equation*}
である。$B \to C$ は $A$ だから$(3)$が成立する。
(b) $P_1, \cdots , P_m$ が真、$P_{m+1}, \cdots , P_n$ が偽のときに $A$ が偽ならば、このとき $B$ が真かつ $C$ が偽であるから、
\begin{eqnarray*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} &\vdash& B \\
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} &\vdash& \lnot C
\end{eqnarray*}
であり、さらに [T10] より $\vdash B \to (\lnot C \to \lnot (B \to C))$ だから、
\begin{equation*}
\{ P_1, \cdots , P_m, \lnot P_{m+1}, \cdots , \lnot P_n \} \vdash \lnot (B \to C)
\end{equation*}
である。$B \to C$ は $A$ だから$(4)$が成立する。
以上より、全ての論理式 $A$ に対して補題が証明できた。
□
この補題を使って、本記事の目的である次の定理を証明します。
【定理11】$\models A$ ならば $\vdash A$ である。すなわちトートロジーは全て論理の定理である。
(証明)
$\models A$ とする。$A$ を構成する原始命題を全て取り出し $P_1, P_2, \cdots , P_n$ とすると、これらの真理値がどのように割り当てられても $A$ は真である。特に $P_n$ に注目すると、【補題10】より、
\begin{eqnarray*}
\{ P_1, \cdots , P_{n-1}, P_n \} &\vdash& A \\
\{ P_1, \cdots , P_{n-1}, \lnot P_n \} &\vdash& A
\end{eqnarray*}
である。これから演繹定理より、
\begin{eqnarray*}
\{ P_1, \cdots , P_{n-1} \} &\vdash& P_n \to A \\
\{ P_1, \cdots , P_{n-1} \} &\vdash& \lnot P_n \to A
\end{eqnarray*}
となる。一方 [T8] より、
\begin{equation*}
\vdash (P_n \to A) \to ((\lnot P_n \to A) \to A)
\end{equation*}
であるから、
\begin{equation*}
\{ P_1, \cdots , P_{n-2}, P_{n-1} \} \vdash A
\end{equation*}
が得られる。同様に、
\begin{eqnarray*}
\{ P_1, \cdots , P_{n-2}, \lnot P_{n-1}, P_n \} &\vdash& A \\
\{ P_1, \cdots , P_{n-2}, \lnot P_{n-1}, \lnot P_n \} &\vdash& A
\end{eqnarray*}
から
\begin{equation*}
\{ P_1, \cdots , P_{n-2}, \lnot P_{n-1} \} \vdash A
\end{equation*}
が得られる。従って、
\begin{eqnarray*}
\{ P_1, \cdots , P_{n-2}, P_{n-1} \} \vdash A \\
\{ P_1, \cdots , P_{n-2}, \lnot P_{n-1} \} \vdash A
\end{eqnarray*}
である。以下この操作を次々繰り返すと、最終的に
\begin{equation*}
\vdash A
\end{equation*}
が得られる。
□
たった3種類の公理系と1つの推論規則から全てのトートロジーが形式的に証明できることが、これで確認できました。



