前の10件 | -
札沼線廃止区間から石狩平野をバスで走る [バス]
ゴールデンウィークに久しぶりの北海道旅行を楽しみました。基本はレンタカーですが、1日だけ札幌周辺を鉄道とバスで回ってきました。
札沼線が短縮された終点近くの当別から札沼線廃止代替バスで月形まで行き、そこから石狩川を越えて岩見沢までのルートです。
(一部ログが途切れてジャンプしています。)
札幌からJR札沼線で終点の北海道医療大学まで乗車。ここまで沿線はほぼ住宅地が続いています。

4年前まではこの先の新十津川まで列車が走っていましたが、現在はここで途切れています。

この駅前は北海道医療大学しかないと言ってよく、バスの発車まで過ごす場所がないので、一つ手前の当別まで戻ります。


月形へのバスは当別駅前から出ています。この駅前もカフェなど過ごせる場所は特にないですが、街中をブラブラ歩いたり、駅近くのパン屋で買ったカレーパンを食べたりしてバスを待ちました。




当別駅周辺の住宅地を回ってから、国道275号線に入って、札沼線の廃線跡に並行して走ります。





駅舎やホームが残る月ヶ岡駅跡に立ち寄り、さらに275号線を進むと、月形の市街地に入ります。



終点は月形駅前(旧石狩月形駅跡前)ですが、手前の月形役場で下車しました。

この役場の付近には、明治から大正にかけて存在した樺戸集治監の建物が「月形樺戸博物館」として公開されています。内部は写真撮影不可なので紹介できませんが、囚人を道路建設などで強制労働に動員した負の歴史も説明しながら、こういう施設の必要性や歴代典獄(刑務所長)の紹介といった説明もあって、複雑な気持ちになる面白い博物館です。




石狩月形駅跡は、駅舎も解体されて整備はこれからといった風情です。なぜかホーム上に発条転轍機が移設されていたりします。バス停標柱が3本ポツンと立っています。




土休日は1日3本しか走らない北海道中央バスの岩見沢行に乗ります。

樺戸集治監の囚人が建設した「峰延道路」を走って石狩川を越えます。


広々とした石狩平野を走ります。


岩見沢市に編入された北村の中心地を通り、牧場や防風林を見ながら走ります。




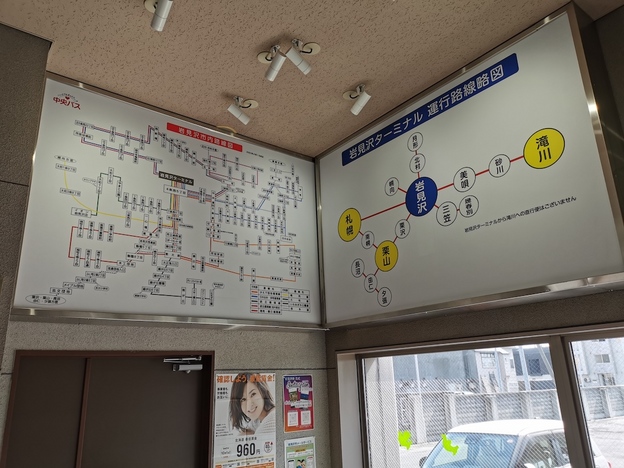
JRの線路を越えて岩見沢の市街地に入り、終点の岩見沢ターミナル(岩見沢駅前)に到着です。


岩見沢バスターミナルは、本数は少なくなったものの、駅に隣接して各地へのバス路線が発着する基幹ターミナルになっています。

JRの普通電車で札幌へ戻りました。

憧れの北海道の路線バスに乗って芒洋とした大地を走り抜け、また廃線跡や興味深い博物館も見学できて、満足の1日でした。
「路線バス歩き」のすすめ(目次)へ
札沼線が短縮された終点近くの当別から札沼線廃止代替バスで月形まで行き、そこから石狩川を越えて岩見沢までのルートです。
(一部ログが途切れてジャンプしています。)
札幌からJR札沼線で終点の北海道医療大学まで乗車。ここまで沿線はほぼ住宅地が続いています。

4年前まではこの先の新十津川まで列車が走っていましたが、現在はここで途切れています。

この駅前は北海道医療大学しかないと言ってよく、バスの発車まで過ごす場所がないので、一つ手前の当別まで戻ります。


月形へのバスは当別駅前から出ています。この駅前もカフェなど過ごせる場所は特にないですが、街中をブラブラ歩いたり、駅近くのパン屋で買ったカレーパンを食べたりしてバスを待ちました。




当別駅周辺の住宅地を回ってから、国道275号線に入って、札沼線の廃線跡に並行して走ります。





駅舎やホームが残る月ヶ岡駅跡に立ち寄り、さらに275号線を進むと、月形の市街地に入ります。



終点は月形駅前(旧石狩月形駅跡前)ですが、手前の月形役場で下車しました。

この役場の付近には、明治から大正にかけて存在した樺戸集治監の建物が「月形樺戸博物館」として公開されています。内部は写真撮影不可なので紹介できませんが、囚人を道路建設などで強制労働に動員した負の歴史も説明しながら、こういう施設の必要性や歴代典獄(刑務所長)の紹介といった説明もあって、複雑な気持ちになる面白い博物館です。




石狩月形駅跡は、駅舎も解体されて整備はこれからといった風情です。なぜかホーム上に発条転轍機が移設されていたりします。バス停標柱が3本ポツンと立っています。




土休日は1日3本しか走らない北海道中央バスの岩見沢行に乗ります。

樺戸集治監の囚人が建設した「峰延道路」を走って石狩川を越えます。


広々とした石狩平野を走ります。


岩見沢市に編入された北村の中心地を通り、牧場や防風林を見ながら走ります。




JRの線路を越えて岩見沢の市街地に入り、終点の岩見沢ターミナル(岩見沢駅前)に到着です。


岩見沢バスターミナルは、本数は少なくなったものの、駅に隣接して各地へのバス路線が発着する基幹ターミナルになっています。


JRの普通電車で札幌へ戻りました。

憧れの北海道の路線バスに乗って芒洋とした大地を走り抜け、また廃線跡や興味深い博物館も見学できて、満足の1日でした。
「路線バス歩き」のすすめ(目次)へ
京都から大津へ「山中越」をバス乗り継ぎで走破 [バス]
比叡山地に阻まれた京都と大津を結ぶ道路は、南から国道1号線(五条通)、三条通、山中越とありますが、北に行くほど厳しい山越えになります。その一番厳しい「山中越」も路線バスで通り抜けることができますが、直通路線はなく、峠付近にある「比叡平ニュータウン」へ京都からも大津からも京阪バスの路線があり、乗り継ぐことによって通り抜けができるようになっています。
とはいえ、その京阪バスも年々本数を減らしており、そのうち通り抜けが不可能になるおそれもあるので、今のうちに乗ってくることにしました。
東山三条から比叡平行に乗車。本当は始発の三条京阪から乗りたかったのですが、たまたま事故で京阪電車が止まっていたため、東大路を走る市バスに乗って東山三条で乗りかえました。

東大路を北上し、吉田寮の立看板が目立つ京都大学前を通ります。


百万遍で東に向きを変え、大文字山が見える銀閣寺道交差点を通ります。

北白川仕伏町を過ぎると、カーブが多くて狭い山中越になります。


山中町ではさらに狭い集落の道を通り抜けます。


本道に戻ったかと思うと、すぐに比叡平ニュータウンの入口になり、バスは中に入っていきます。


かなり広いニュータウンの奥まで入って、ようやく終点の比叡平です。

バスの転回場には降り場しかなく、乗り場は少し戻った場所にありました。

京都と大津の両方にバスが走っていますが、土休日は京都行最終が13時台で終わり。大津行きも17時台で終わりで、便利とは言えません。

大津京駅行きのバスまで1時間ほどあるので、ぶらぶら歩きます。
比叡山が見える気持ちのいい住宅地です。

夜は鹿が出るそうで、ゴミ置き場に注意書きがありました。

昔は米屋だったらしいが今は廃業。食料品などが買える店はニュータウンの入口にあるコンビニだけです。移動販売車は来るようですが。

トイレに行きたくなったのですが、ニュータウン内には公衆トイレがありません。郵便局は土休日休みだし、公民館のトイレも閉まっていて入れませんでした。


仕方がないのでニュータウンの外に出て、比叡山ドライブウェイ入口料金所のトイレを借りました。

ニュータウン内に戻り、三丁目東のバス停から大津京駅行きに乗ります。


琵琶湖をチラチラ見ながら山中越を下っていきます。




近江神宮のそばを通り過ぎると、まもなくタワマンの目立つ大津京駅に到着です。


JR湖西線で帰路につきました。

カーブの多い峠道を通り抜ける楽しい路線ですが、比叡平ニュータウンの人口も減りつつあるようなので、いつまで走り続けられるか心配です。
「路線バス歩き」のすすめ(目次)へ
とはいえ、その京阪バスも年々本数を減らしており、そのうち通り抜けが不可能になるおそれもあるので、今のうちに乗ってくることにしました。
東山三条から比叡平行に乗車。本当は始発の三条京阪から乗りたかったのですが、たまたま事故で京阪電車が止まっていたため、東大路を走る市バスに乗って東山三条で乗りかえました。

東大路を北上し、吉田寮の立看板が目立つ京都大学前を通ります。


百万遍で東に向きを変え、大文字山が見える銀閣寺道交差点を通ります。

北白川仕伏町を過ぎると、カーブが多くて狭い山中越になります。


山中町ではさらに狭い集落の道を通り抜けます。


本道に戻ったかと思うと、すぐに比叡平ニュータウンの入口になり、バスは中に入っていきます。


かなり広いニュータウンの奥まで入って、ようやく終点の比叡平です。

バスの転回場には降り場しかなく、乗り場は少し戻った場所にありました。

京都と大津の両方にバスが走っていますが、土休日は京都行最終が13時台で終わり。大津行きも17時台で終わりで、便利とは言えません。

大津京駅行きのバスまで1時間ほどあるので、ぶらぶら歩きます。
比叡山が見える気持ちのいい住宅地です。

夜は鹿が出るそうで、ゴミ置き場に注意書きがありました。

昔は米屋だったらしいが今は廃業。食料品などが買える店はニュータウンの入口にあるコンビニだけです。移動販売車は来るようですが。

トイレに行きたくなったのですが、ニュータウン内には公衆トイレがありません。郵便局は土休日休みだし、公民館のトイレも閉まっていて入れませんでした。


仕方がないのでニュータウンの外に出て、比叡山ドライブウェイ入口料金所のトイレを借りました。

ニュータウン内に戻り、三丁目東のバス停から大津京駅行きに乗ります。


琵琶湖をチラチラ見ながら山中越を下っていきます。




近江神宮のそばを通り過ぎると、まもなくタワマンの目立つ大津京駅に到着です。


JR湖西線で帰路につきました。

カーブの多い峠道を通り抜ける楽しい路線ですが、比叡平ニュータウンの人口も減りつつあるようなので、いつまで走り続けられるか心配です。
「路線バス歩き」のすすめ(目次)へ
わかってない奴がわかったつもりで書き留める超準解析(その20) [数学]
【超準解析について生半可な知識しかない僕が、わかったつもりの内容をちょっとずつ書き留めていきます。不正確な内容や誤りもあることをご承知ください。】
(20) 直積空間とカントール空間
本記事では、直積空間を超準的に扱うことを考えます。
1. 直積空間のモナド
$I$ を添字集合とする集合族 $\{ \, X_i \, \}_{i \in I}$ があるとき、直積集合 $\prod_{i \in I} X_i$ が定まります(超冪を構成した時に用いた $I$ とは無関係です)。これは、$I$ から $\bigcup_{i \in I} X_i$ への写像 $x$ のうち、
\begin{equation*}
\forall i \in I \,( x(i) \in X_i )
\end{equation*}
をみたすものの全体です。特に $X_i$ が全て同じ $X$ の場合は、$\prod_{i \in I} X$ は $I$ から $X$ への写像の全体となり、本記事ではこれを ${}^IX$ で表します( $X^I$ で表す流儀もあります)。
以下では $\prod_{i \in I} X_i$ を簡単に $\hat{X}$ とおいて、$\hat{X}$ の超準モデル ${}^*\hat{X}$ について考えます。
一般に、集合 $W$ の全ての元が集合 $X$ から集合 $Y$ への写像であるとき、写像の定義より
\begin{equation*}
\forall w \in W \, ( \forall z \in w \, \exists x \in X \, \exists y \in Y \, ( z = \langle x, y \rangle ) \land \forall x \in X \, \exists ! y \in Y \, ( \langle x, y \rangle \in w ) )
\end{equation*}
が成り立つので、移行原理より、
\begin{equation*}
\forall w \in {}^*W \, ( \forall z \in w \, \exists x \in {}^*X \, \exists y \in {}^*Y \, ( z = \langle x, y \rangle ) \land \forall x \in {}^*X \, \exists ! y \in {}^*Y \, ( \langle x, y \rangle \in w ) )
\end{equation*}
が成り立ち、従って ${}^*W$ の全ての元は集合 ${}^*X$ から集合 ${}^*Y$ への写像になります。そこで、$\hat{X}$ の元は $I$ から $\bigcup_{i \in I} X_i$ への写像なので、${}^*\hat{X}$ の元は ${}^*I$ から ${}^*(\bigcup_{i \in I} X_i)$ への写像です。任意の $i \in I$ に対して
\begin{equation*}
\forall x \in \hat{X} \,( x(i) \in X_i )
\end{equation*}
が成り立つので、移行原理より任意の $i \in I$ に対して
\begin{equation} \tag{1}
\forall x \in {}^*\hat{X} \,( x(i) \in {}^*X_i )
\end{equation}
が成り立ちます。
ここで、各 $X_i$ が開集合族 $\mathcal{O}_i$ によって位相空間となっているとすると、直積集合 $\hat{X}$ の部分集合の族
は $\hat{X}$ の開基の条件を満たすので、これによって $\hat{X}$ の位相(直積位相)が定まります。このとき、モナドについて次の定理が成立します。
(証明)
($\rightarrow$ の証明)ある $u \in \mathrm{monad}_{\hat{X}}(x)$ が $\lnot ( \forall i \in I \, ( u(i) \in \mathrm{monad}_{X_i}(x(i)) ) )$ をみたすと仮定して矛盾を導く。このとき $\exists i \in I \, ( u(i) \notin \mathrm{monad}_{X_i}(x(i)) )$ であるから、これをみたす $i$ をひとつ取って $i_0$ とおく。$u(i_0) \notin \mathrm{monad}_{X_{i_0}}(x(i_0))$ だから、$X_{i_0}$ における $x(i_0)$ の近傍 $A_{i_0}$ で $u(i_0) \notin {}^*A_{i_0}$ となるものがとれる。$i \neq i_0$ に対して $A_i = X_i$ として $\hat{A} = \prod_{i \in I} A_i$ とおくと、$\hat{A}$ は $\hat{X}$ における $x$ の近傍になるから、$u \in \mathrm{monad}_{\hat{X}}(x)$ より $u \in {}^*\hat{A}$ である。しかし $\forall z \in \hat{A} \, ( z(i_0) \in A_{i_0} )$ と移行原理より $\forall z \in {}^*\hat{A} \, ( z(i_0) \in {}^*A_{i_0} )$ だから、$u(i_0) \in {}^*A_{i_0}$ でなければならず、矛盾を生じる。
($\leftarrow$ の証明)ある $u \in {}^*\hat{X}$ が $\forall i \in I \, ( u(i) \in \mathrm{monad}_{X_i}(x(i)) )$ かつ $u \notin \mathrm{monad}_{\hat{X}}(x)$ と仮定して矛盾を導く。このとき $\hat{X}$ における $x$ の近傍 $\hat{A}$ で $u \notin {}^*\hat{A}$ となるものがとれる。直積位相の定義から、$\hat{A} \supseteq \hat{B} = \prod_{i \in I} B_i$ で各 $B_i$ は $x(i)$ の開近傍、かつ有限個の $i$ を除き $B_i = X_i$ となるような $\hat{B}$ がある。その有限個の $i$ を $i_1, i_2, \cdots , i_n$ とおくと、
\begin{equation*}
\forall z \in \hat{X} \, ( z \in \hat{B} \leftrightarrow z(i_1) \in B_{i_1} \land z(i_2) \in B_{i_2} \land \cdots \land z(i_n) \in B_{i_n} )
\end{equation*}
であり、移行原理より、
\begin{equation*}
\forall z \in {}^*\hat{X} \, ( z \in {}^*\hat{B} \leftrightarrow z(i_1) \in {}^*B_{i_1} \land z(i_2) \in {}^*B_{i_2} \land \cdots \land z(i_n) \in {}^*B_{i_n} )
\end{equation*}
である。一方、$\forall i \in I \, ( u(i) \in \mathrm{monad}_{X_i}(x(i)) )$ かつ各 $B_i$ が $x(i)$ の近傍であることから、
\begin{equation*}
u(i_1) \in {}^*B_{i_1} \land u(i_2) \in {}^*B_{i_2} \land \cdots \land u(i_n) \in {}^*B_{i_n}
\end{equation*}
これより $u \in {}^*\hat{B} \subseteq {}^*\hat{A}$ となって $u \notin {}^*\hat{A}$ と矛盾する。□
この定理から、特に $I$ が有限集合のときには次が成立します(第19回【補題1】と数学的帰納法を用いても証明できます)。
(証明)$I$ が有限集合のときは、${}^*I = I$ かつ ${}^*(\bigcup_{i \in I} X_i) = \bigcup_{i \in I} {}^*X_i$ であるから、${}^*\hat{X}$ の元は $I$ から $\bigcup_{i \in I} {}^*X_i$ への写像である。従って【定理1】より$(2)$が成り立つ。□
2. 直積空間の諸性質
【定理1】を使うと、位相空間におけるいくつかの性質が直積空間にも引き継がれることが機械的に証明できます。まずは閉集合から。
(証明)$\hat{A} = \prod_{i \in I} A_i$ とおく。
$\hat{A}$ が閉集合でないと仮定すると、第17回【定理3】 ii) より $\mathrm{monad}_{\hat{X}}(x) \cap {}^*\hat{A} \neq \emptyset$ となる $x \in \hat{X} \setminus \hat{A}$ が存在する。$x \notin \hat{A}$ だから、ある $i_0 \in I$ について $x(i_0) \notin A_{i_0}$ である。一方、ある $u \in {}^*\hat{X}$ に対して $u \in \mathrm{monad}_{\hat{X}}(x) \cap {}^*\hat{A}$ であるから、【定理1】より $u(i_0) \in \mathrm{monad}_{X_{i_0}}(x(i_0))$ である。さらに$(1)$を導いた移行原理を同様に $\hat{A}$ に適用すると $u(i_0) \in {}^*A_{i_0}$ がいえるから、$u(i_0) \in \mathrm{monad}_{X_{i_0}}(x(i_0)) \cap {}^*A_{i_0}$ より $\mathrm{monad}_{X_{i_0}}(x(i_0)) \cap {}^*A_{i_0} \neq \emptyset$ である。$A_{i_0}$ は閉集合で $x(i_0) \in X_{i_0}$ だから、第17回【定理3】 ii) より $x(i_0) \in A_{i_0}$ となり、矛盾を生じる。□
なお、開集合の直積は必ずしも開集合にはなりません。
次にコンパクト性について。
(証明)任意に $u \in {}^*\hat{X}$ をとる。任意の $i \in I$ に対して $u(i) \in {}^*X_i$ であり、$X_i$ がコンパクトだから、第17回【定理5】よりある $x_i \in X_i$ に対して $u(i) \in \mathrm{monad}_{X_i}(x_i)$ となる。$\forall i \in I \, (x(i) = x_i)$ となるように $x \in \hat{X}$ を定めると、
\begin{equation*}
\forall i \in I \, ( u(i) \in \mathrm{monad}_{X_i}(x(i)) )
\end{equation*}
であるから、【定理1】より $u \in \mathrm{monad}_{\hat{X}}(x)$ である。従って再び第17回【定理5】より $\hat{X}$ はコンパクトである。□
同様にして、分離公理に関する次の定理も証明できます。
(証明)
i) $\hat{X}$ が $\mathrm{T}_1$ でないと仮定する。第17回【定理4】 i) より、$x \neq y \land y \in \mathrm{monad}_{\hat{X}}(x)$ となる $x,y \in \hat{X}$ が存在する。$x \neq y$ だから、ある $i_0 \in I$ に対して $x(i_0) \neq y(i_0)$ となるが、$x(i_0), y(i_0) \in X_{i_0}$ かつ $X_{i_0}$ が $\mathrm{T}_1$ だから、第17回【定理4】 i) より $y(i_0) \notin \mathrm{monad}_{X_{i_0}}(x(i_0))$ である。一方、$y \in \mathrm{monad}_{\hat{X}}(x)$ と【定理1】より $y(i_0) \in \mathrm{monad}_{X_{i_0}}(x(i_0))$ が従うから、矛盾を生じる。
ii) $\hat{X}$ が $\mathrm{T}_2$ でないと仮定する。第17回【定理4】 ii) より、$x \neq y \land \mathrm{monad}_{\hat{X}}(x) \cap \mathrm{monad}_{\hat{X}}(y) \neq \emptyset$ となる $x,y \in \hat{X}$ が存在する。$x \neq y$ だから、ある $i_0 \in I$ に対して $x(i_0) \neq y(i_0)$ となるが、$x(i_0), y(i_0) \in X_{i_0}$ かつ $X_{i_0}$ が $\mathrm{T}_2$ だから、第17回【定理4】 ii) より $\mathrm{monad}_{X_{i_0}}(x(i_0)) \cap \mathrm{monad}_{X_{i_0}}(y(i_0)) = \emptyset$ である。一方、$\mathrm{monad}_{\hat{X}}(x) \cap \mathrm{monad}_{\hat{X}}(y) \neq \emptyset$ より $u \in \mathrm{monad}_{\hat{X}}(x) \cap \mathrm{monad}_{\hat{X}}(y)$ となる $u \in {}^*\hat{X}$ が存在し、【定理1】より $u(i_0) \in \mathrm{monad}_{X_{i_0}}(x(i_0)) \cap \mathrm{monad}_{X_{i_0}}(y(i_0))$ が従うから、$\mathrm{monad}_{X_{i_0}}(x(i_0)) \cap \mathrm{monad}_{X_{i_0}}(y(i_0)) \neq \emptyset$ となって矛盾を生じる。□
また、連続写像に関する定理を用いると、次が証明できます。
(証明)任意に $x \in \hat{X}$ と $u \in \mathrm{monad}_{\hat{X}}(x)$ をとる。任意に $i \in I $ をとると、【定理1】より $u(i) \in \mathrm{monad}_{X_i}(x(i))$ である。一方、
\begin{equation*}
\forall z \in \hat{X} \, ( p_i(z) = z(i) )
\end{equation*}
と移行原理より、
\begin{equation*}
\forall z \in {}^*\hat{X} \, ( {}^*p_i(z) = z(i) )
\end{equation*}
であるから、${}^*p_i(u) = u(i) \in \mathrm{monad}_{X_i}(x(i)) = \mathrm{monad}_{X_i}(p_i(x))$ となり、第19回【定理2】より $p_i$ は $\hat{X}$ で連続である。□
どの性質も、極めて機械的に証明できることがわかります。
3. カントール空間
本節の議論の応用例として、カントール空間について考察してみます。
自然数の全体 $\mathbb{N}$ から$2$元集合 $\{ \, 0, 1 \, \}$(この集合を $2$ で表します) への写像の全体 ${}^{\mathbb{N}}2 \, ( \, = \prod_{i \in \mathbb{N}} 2 \, )$ を考え、$2$ に離散位相を入れて ${}^{\mathbb{N}}2$ を直積位相空間と考えます。明らかに $2$ はコンパクトだから、【定理4】(チコノフの定理)より ${}^{\mathbb{N}}2$ もコンパクトです。一方、区間 $[ 0, 1 ]$ に属する実数のうち$3$進法無限小数表記で$0$と$2$だけしか現れないようなものの全体 $\mathcal{C}$ は「カントール集合」と呼ばれますが(下図を参照)、これを$1$次元ユークリッド空間 $\mathbb{R}$ の部分位相空間と考えると、$\mathbb{R}$ において有界閉集合なのでこれもコンパクトです。これら ${}^{\mathbb{N}}2$ と $\mathcal{C}$ は実は同相であり、どちらも「カントール空間」と呼ばれる位相空間の一つです。このことを以下で超準的手法を用いて証明します。

$x \in {}^{\mathbb{N}}2$ に対し、無限級数 $\displaystyle \sum_{i = 0}^\infty 2 x(i) / 3^{i+1}$ は $\mathbb{R}$ 内で収束するので、その和となる実数値を対応させる写像を $f$ とおくと、$f$ は ${}^{\mathbb{N}}2$ から $\mathcal{C}$ への全単射になります。従ってこの $f$ が連続写像であることを証明すれば、${}^{\mathbb{N}}2$ がコンパクト、$\mathbb{R}$ がハウスドルフ(従って $\mathcal{C}$ もハウスドルフ)なので、第19回【定理6】によって ${}^{\mathbb{N}}2$ と $\mathcal{C}$ が同相であることが示されます。第19回【定理2】を使ってこれを示すのですが、その概略は次のとおりです。
任意に $x \in {}^{\mathbb{N}}2$ をとり、その $x$ に対して任意に $u \in \mathrm{monad}_{{}^{\mathbb{N}}2}(x)$ をとります。$u \in {}^*( {}^{\mathbb{N}}2 )$ なので $u$ は ${}^*\mathbb{N}$ から $2 \, ( ={}^*2 )$ への写像であり、$i \in \mathbb{N}$ に対しては【定理1】より($2$ には離散位相が入るから) $u(i) \in \mathrm{monad}_2(x(i)) = \{ x(i) \}$ なので $u(i) = x(i)$ になります。この $u$ に対する ${}^*f(u)$ は超実数体 ${}^*\mathbb{R}$ における無限級数の和として $\displaystyle {}^*f(u) = {}^*\sum_{i = 0}^\infty 2 u(i) / 3^{i+1}$ となるので、その標準部分は実数体 $\mathbb{R}$ における無限級数の和として
\begin{equation} \tag{3}
\mathrm{st}({}^*f(u)) = \sum_{i = 0}^\infty 2 u(i) / 3^{i+1} = \sum_{i = 0}^\infty 2 x(i) / 3^{i+1} = f(x)
\end{equation}
となります。従って第18回【定理1】より ${}^*f(u) \in \mathrm{monad}_\mathbb{R}(f(x)) \cap {}^*\mathcal{C} = \mathrm{monad}_\mathcal{C}(f(x))$ となるので、第19回【定理2】より $f$ は任意の $x \in {}^{\mathbb{N}}2$ で連続となり、証明が完了します。
この概略の最後の部分(「超実数体 ${}^*\mathbb{R}$ における無限級数の和」以降)は少々直感的にすぎるので、もう少し精密に考えてみます。$z \in {}^{\mathbb{N}}2$ に対する無限級数 $\displaystyle \sum_{i = 0}^\infty 2 z(i) / 3^{i+1}$ は常に $f(z)$ に収束するので、
\begin{equation} \tag{4}
\forall z \in {}^{\mathbb{N}}2 \, \forall \epsilon \in \mathbb{R}^+ \, \exists n \in \mathbb{N} \, \forall k \in \mathbb{N} \, ( k \ge n \to \left| f(z) - \sum_{i = 0}^k 2 z(i) / 3^{i+1} \right| < \epsilon)
\end{equation}
が成り立ちます( $\mathbb{R}^+$ は正実数の全体)。すると移行原理によって、
\begin{equation} \tag{5}
\forall z \in {}^*( {}^{\mathbb{N}}2 ) \, \forall \epsilon \in {}^*\mathbb{R}^+ \, \exists n \in {}^*\mathbb{N} \, \forall k \in {}^*\mathbb{N} \, ( k \ge n \to \left| {}^*f(z) - {}^*\sum_{i = 0}^k 2 z(i) / 3^{i+1} \right| < \epsilon)
\end{equation}
が成り立ちます。そこで $u \in {}^*( {}^{\mathbb{N}}2 )$ に対して任意に正実数 $\epsilon$ をとり、$\mathbb{R}$ における無限級数 $\displaystyle \sum_{i = 0}^\infty 2 u(i) / 3^{i+1}$ の和を $s$ とおくと、$(4)$より十分大きな自然数 $m$ をとると、
\begin{equation*}
\left| s - \sum_{i = 0}^m 2 u(i) / 3^{i+1} \right| < \epsilon
\end{equation*}
が成り立ち、また$(5)$より十分大きな超自然数 $n ( > m)$ をとると、
\begin{equation*}
\left| {}^*f(u) - {}^*\sum_{i = 0}^n 2 u(i) / 3^{i+1} \right| < \epsilon
\end{equation*}
が成り立ちます。そして、
\begin{eqnarray*}
\left| {}^*\sum_{i = 0}^n 2 u(i) / 3^{i+1} - \sum_{i = 0}^m 2 u(i) / 3^{i+1} \right| &=& {}^*\sum_{i = m + 1}^n 2 u(i) / 3^{i+1} \le {}^*\sum_{i = m + 1}^n 2 / 3^{i+1} = \frac{1}{3^{m+1}}-\frac{1}{3^{n+1}} \\
&<& \frac{1}{3^{m+1}}
\end{eqnarray*}
であることから、$m$ を十分大きくとると、
\begin{equation*}
\left| {}^*\sum_{i = 0}^n 2 u(i) / 3^{i+1} - \sum_{i = 0}^m 2 u(i) / 3^{i+1} \right| < \epsilon
\end{equation*}
となるようにできます。これらより、
\begin{eqnarray*}
&&\left| {}^*f(u) - s \right| \\
&\le& \left| {}^*f(u) - {}^*\sum_{i = 0}^n 2 u(i) / 3^{i+1} \right| + \left| {}^*\sum_{i = 0}^n 2 u(i) / 3^{i+1} - \sum_{i = 0}^m 2 u(i) / 3^{i+1} \right| + \left| \sum_{i = 0}^m 2 u(i) / 3^{i+1} -s \right| \\
&<& 3 \epsilon
\end{eqnarray*}
となり、$\epsilon \in \mathbb{R}^+$ は任意なので $\left| {}^*f(u) - s \right| \approx 0$ すなわち $\mathrm{st}({}^*f(u)) = s$ が成り立ちます。これで証明中の($3$)の最初の等号部分が厳密に示されました。
以上で、少し回りくどかったですが、超準的手法を用いて2種類のカントール空間 ${}^{\mathbb{N}}2$ と $\mathcal{C}$ が同相であることを示すことができました。
注意すべきは、「 ${}^{\mathbb{N}}2$ の元は $0$ または $1$ の無限列なので、2進法の無限小数と対応するから、${}^{\mathbb{N}}2$ と実数の区間 $[ 0, 1 ]$ が同相になるのではないのか?」と早とちりしてはいけないということです。$x \in {}^{\mathbb{N}}2$ に無限級数 $\displaystyle \sum_{i = 0}^\infty x(i) / 2^{i+1}$ を対応させると、例えば2進法無限小数 $0.011111 \cdots$ は $0.100000 \cdots$ と実数として等しいので、この対応では ${}^{\mathbb{N}}2$ と $[ 0, 1 ]$ が1対1になりません。一方、先ほどの証明の方法で ${}^{\mathbb{N}}2$ の元に3進法無限小数を対応させると、例えば $0.022222 \cdots = 0.100000 \cdots$ ですが、後者は $1$ を含むので ${}^{\mathbb{N}}2$ の元に対応せず、従ってこちらの対応だと ${}^{\mathbb{N}}2$ と $\mathcal{C}$ が1対1になるのです。
(続く)(前記事)(目次)
(20) 直積空間とカントール空間
本記事では、直積空間を超準的に扱うことを考えます。
1. 直積空間のモナド
$I$ を添字集合とする集合族 $\{ \, X_i \, \}_{i \in I}$ があるとき、直積集合 $\prod_{i \in I} X_i$ が定まります(超冪を構成した時に用いた $I$ とは無関係です)。これは、$I$ から $\bigcup_{i \in I} X_i$ への写像 $x$ のうち、
\begin{equation*}
\forall i \in I \,( x(i) \in X_i )
\end{equation*}
をみたすものの全体です。特に $X_i$ が全て同じ $X$ の場合は、$\prod_{i \in I} X$ は $I$ から $X$ への写像の全体となり、本記事ではこれを ${}^IX$ で表します( $X^I$ で表す流儀もあります)。
以下では $\prod_{i \in I} X_i$ を簡単に $\hat{X}$ とおいて、$\hat{X}$ の超準モデル ${}^*\hat{X}$ について考えます。
一般に、集合 $W$ の全ての元が集合 $X$ から集合 $Y$ への写像であるとき、写像の定義より
\begin{equation*}
\forall w \in W \, ( \forall z \in w \, \exists x \in X \, \exists y \in Y \, ( z = \langle x, y \rangle ) \land \forall x \in X \, \exists ! y \in Y \, ( \langle x, y \rangle \in w ) )
\end{equation*}
が成り立つので、移行原理より、
\begin{equation*}
\forall w \in {}^*W \, ( \forall z \in w \, \exists x \in {}^*X \, \exists y \in {}^*Y \, ( z = \langle x, y \rangle ) \land \forall x \in {}^*X \, \exists ! y \in {}^*Y \, ( \langle x, y \rangle \in w ) )
\end{equation*}
が成り立ち、従って ${}^*W$ の全ての元は集合 ${}^*X$ から集合 ${}^*Y$ への写像になります。そこで、$\hat{X}$ の元は $I$ から $\bigcup_{i \in I} X_i$ への写像なので、${}^*\hat{X}$ の元は ${}^*I$ から ${}^*(\bigcup_{i \in I} X_i)$ への写像です。任意の $i \in I$ に対して
\begin{equation*}
\forall x \in \hat{X} \,( x(i) \in X_i )
\end{equation*}
が成り立つので、移行原理より任意の $i \in I$ に対して
\begin{equation} \tag{1}
\forall x \in {}^*\hat{X} \,( x(i) \in {}^*X_i )
\end{equation}
が成り立ちます。
ここで、各 $X_i$ が開集合族 $\mathcal{O}_i$ によって位相空間となっているとすると、直積集合 $\hat{X}$ の部分集合の族
$\{ \, \prod_{i \in I} U_i \, \mid \, \forall i \in I \, (U_i \in \mathcal{O}_i)$ かつ有限個の $i$ を除き $U_i = X_i \, \}$
は $\hat{X}$ の開基の条件を満たすので、これによって $\hat{X}$ の位相(直積位相)が定まります。このとき、モナドについて次の定理が成立します。
【定理1】$\hat{X} \, (= \prod_{i \in I} X_i)$ の任意の点 $x$ に対して、次が成立する。
\begin{equation*}
\forall u \in {}^*\hat{X}\, ( u \in \mathrm{monad}_{\hat{X}}(x) \leftrightarrow \forall i \in I \, ( u(i) \in \mathrm{monad}_{X_i}(x(i)) ) )
\end{equation*}
(証明)
($\rightarrow$ の証明)ある $u \in \mathrm{monad}_{\hat{X}}(x)$ が $\lnot ( \forall i \in I \, ( u(i) \in \mathrm{monad}_{X_i}(x(i)) ) )$ をみたすと仮定して矛盾を導く。このとき $\exists i \in I \, ( u(i) \notin \mathrm{monad}_{X_i}(x(i)) )$ であるから、これをみたす $i$ をひとつ取って $i_0$ とおく。$u(i_0) \notin \mathrm{monad}_{X_{i_0}}(x(i_0))$ だから、$X_{i_0}$ における $x(i_0)$ の近傍 $A_{i_0}$ で $u(i_0) \notin {}^*A_{i_0}$ となるものがとれる。$i \neq i_0$ に対して $A_i = X_i$ として $\hat{A} = \prod_{i \in I} A_i$ とおくと、$\hat{A}$ は $\hat{X}$ における $x$ の近傍になるから、$u \in \mathrm{monad}_{\hat{X}}(x)$ より $u \in {}^*\hat{A}$ である。しかし $\forall z \in \hat{A} \, ( z(i_0) \in A_{i_0} )$ と移行原理より $\forall z \in {}^*\hat{A} \, ( z(i_0) \in {}^*A_{i_0} )$ だから、$u(i_0) \in {}^*A_{i_0}$ でなければならず、矛盾を生じる。
($\leftarrow$ の証明)ある $u \in {}^*\hat{X}$ が $\forall i \in I \, ( u(i) \in \mathrm{monad}_{X_i}(x(i)) )$ かつ $u \notin \mathrm{monad}_{\hat{X}}(x)$ と仮定して矛盾を導く。このとき $\hat{X}$ における $x$ の近傍 $\hat{A}$ で $u \notin {}^*\hat{A}$ となるものがとれる。直積位相の定義から、$\hat{A} \supseteq \hat{B} = \prod_{i \in I} B_i$ で各 $B_i$ は $x(i)$ の開近傍、かつ有限個の $i$ を除き $B_i = X_i$ となるような $\hat{B}$ がある。その有限個の $i$ を $i_1, i_2, \cdots , i_n$ とおくと、
\begin{equation*}
\forall z \in \hat{X} \, ( z \in \hat{B} \leftrightarrow z(i_1) \in B_{i_1} \land z(i_2) \in B_{i_2} \land \cdots \land z(i_n) \in B_{i_n} )
\end{equation*}
であり、移行原理より、
\begin{equation*}
\forall z \in {}^*\hat{X} \, ( z \in {}^*\hat{B} \leftrightarrow z(i_1) \in {}^*B_{i_1} \land z(i_2) \in {}^*B_{i_2} \land \cdots \land z(i_n) \in {}^*B_{i_n} )
\end{equation*}
である。一方、$\forall i \in I \, ( u(i) \in \mathrm{monad}_{X_i}(x(i)) )$ かつ各 $B_i$ が $x(i)$ の近傍であることから、
\begin{equation*}
u(i_1) \in {}^*B_{i_1} \land u(i_2) \in {}^*B_{i_2} \land \cdots \land u(i_n) \in {}^*B_{i_n}
\end{equation*}
これより $u \in {}^*\hat{B} \subseteq {}^*\hat{A}$ となって $u \notin {}^*\hat{A}$ と矛盾する。□
この定理から、特に $I$ が有限集合のときには次が成立します(第19回【補題1】と数学的帰納法を用いても証明できます)。
【系2】$I$ が有限集合ならば、$\hat{X} \, (= \prod_{i \in I} X_i)$ の任意の点 $x$ に対して、次が成立する。
\begin{equation}
\mathrm{monad}_{\hat{X}}(x) = \prod_{i \in I} \mathrm{monad}_{X_i}(x(i)) \tag{2}
\end{equation}
(証明)$I$ が有限集合のときは、${}^*I = I$ かつ ${}^*(\bigcup_{i \in I} X_i) = \bigcup_{i \in I} {}^*X_i$ であるから、${}^*\hat{X}$ の元は $I$ から $\bigcup_{i \in I} {}^*X_i$ への写像である。従って【定理1】より$(2)$が成り立つ。□
2. 直積空間の諸性質
【定理1】を使うと、位相空間におけるいくつかの性質が直積空間にも引き継がれることが機械的に証明できます。まずは閉集合から。
【定理3】直積空間 $\hat{X} \, (= \prod_{i \in I} X_i)$ において、各 $i \in I$ に対する $X_i$ の閉集合 $A_i$ の直積 $\prod_{i \in I} A_i$ は $\hat{X}$ の閉集合である。
(証明)$\hat{A} = \prod_{i \in I} A_i$ とおく。
$\hat{A}$ が閉集合でないと仮定すると、第17回【定理3】 ii) より $\mathrm{monad}_{\hat{X}}(x) \cap {}^*\hat{A} \neq \emptyset$ となる $x \in \hat{X} \setminus \hat{A}$ が存在する。$x \notin \hat{A}$ だから、ある $i_0 \in I$ について $x(i_0) \notin A_{i_0}$ である。一方、ある $u \in {}^*\hat{X}$ に対して $u \in \mathrm{monad}_{\hat{X}}(x) \cap {}^*\hat{A}$ であるから、【定理1】より $u(i_0) \in \mathrm{monad}_{X_{i_0}}(x(i_0))$ である。さらに$(1)$を導いた移行原理を同様に $\hat{A}$ に適用すると $u(i_0) \in {}^*A_{i_0}$ がいえるから、$u(i_0) \in \mathrm{monad}_{X_{i_0}}(x(i_0)) \cap {}^*A_{i_0}$ より $\mathrm{monad}_{X_{i_0}}(x(i_0)) \cap {}^*A_{i_0} \neq \emptyset$ である。$A_{i_0}$ は閉集合で $x(i_0) \in X_{i_0}$ だから、第17回【定理3】 ii) より $x(i_0) \in A_{i_0}$ となり、矛盾を生じる。□
なお、開集合の直積は必ずしも開集合にはなりません。
次にコンパクト性について。
【定理4】(チコノフの定理)すべての $i \in I$ に対して $X_i$ がコンパクト空間ならば、直積空間 $\hat{X} \, (= \prod_{i \in I} X_i)$ もコンパクトである。
(証明)任意に $u \in {}^*\hat{X}$ をとる。任意の $i \in I$ に対して $u(i) \in {}^*X_i$ であり、$X_i$ がコンパクトだから、第17回【定理5】よりある $x_i \in X_i$ に対して $u(i) \in \mathrm{monad}_{X_i}(x_i)$ となる。$\forall i \in I \, (x(i) = x_i)$ となるように $x \in \hat{X}$ を定めると、
\begin{equation*}
\forall i \in I \, ( u(i) \in \mathrm{monad}_{X_i}(x(i)) )
\end{equation*}
であるから、【定理1】より $u \in \mathrm{monad}_{\hat{X}}(x)$ である。従って再び第17回【定理5】より $\hat{X}$ はコンパクトである。□
同様にして、分離公理に関する次の定理も証明できます。
【定理5】直積空間 $\hat{X} \, (= \prod_{i \in I} X_i)$ について次が成立する。
i) すべての $i \in I$ に対して $X_i$ が $\mathrm{T}_1$ ならば、$\hat{X}$ も $\mathrm{T}_1$ である。
ii) すべての $i \in I$ に対して $X_i$ が $\mathrm{T}_2$(ハウスドルフ)ならば、$\hat{X}$ も $\mathrm{T}_2$(ハウスドルフ)である。
i) すべての $i \in I$ に対して $X_i$ が $\mathrm{T}_1$ ならば、$\hat{X}$ も $\mathrm{T}_1$ である。
ii) すべての $i \in I$ に対して $X_i$ が $\mathrm{T}_2$(ハウスドルフ)ならば、$\hat{X}$ も $\mathrm{T}_2$(ハウスドルフ)である。
(証明)
i) $\hat{X}$ が $\mathrm{T}_1$ でないと仮定する。第17回【定理4】 i) より、$x \neq y \land y \in \mathrm{monad}_{\hat{X}}(x)$ となる $x,y \in \hat{X}$ が存在する。$x \neq y$ だから、ある $i_0 \in I$ に対して $x(i_0) \neq y(i_0)$ となるが、$x(i_0), y(i_0) \in X_{i_0}$ かつ $X_{i_0}$ が $\mathrm{T}_1$ だから、第17回【定理4】 i) より $y(i_0) \notin \mathrm{monad}_{X_{i_0}}(x(i_0))$ である。一方、$y \in \mathrm{monad}_{\hat{X}}(x)$ と【定理1】より $y(i_0) \in \mathrm{monad}_{X_{i_0}}(x(i_0))$ が従うから、矛盾を生じる。
ii) $\hat{X}$ が $\mathrm{T}_2$ でないと仮定する。第17回【定理4】 ii) より、$x \neq y \land \mathrm{monad}_{\hat{X}}(x) \cap \mathrm{monad}_{\hat{X}}(y) \neq \emptyset$ となる $x,y \in \hat{X}$ が存在する。$x \neq y$ だから、ある $i_0 \in I$ に対して $x(i_0) \neq y(i_0)$ となるが、$x(i_0), y(i_0) \in X_{i_0}$ かつ $X_{i_0}$ が $\mathrm{T}_2$ だから、第17回【定理4】 ii) より $\mathrm{monad}_{X_{i_0}}(x(i_0)) \cap \mathrm{monad}_{X_{i_0}}(y(i_0)) = \emptyset$ である。一方、$\mathrm{monad}_{\hat{X}}(x) \cap \mathrm{monad}_{\hat{X}}(y) \neq \emptyset$ より $u \in \mathrm{monad}_{\hat{X}}(x) \cap \mathrm{monad}_{\hat{X}}(y)$ となる $u \in {}^*\hat{X}$ が存在し、【定理1】より $u(i_0) \in \mathrm{monad}_{X_{i_0}}(x(i_0)) \cap \mathrm{monad}_{X_{i_0}}(y(i_0))$ が従うから、$\mathrm{monad}_{X_{i_0}}(x(i_0)) \cap \mathrm{monad}_{X_{i_0}}(y(i_0)) \neq \emptyset$ となって矛盾を生じる。□
また、連続写像に関する定理を用いると、次が証明できます。
【定理6】直積空間 $\hat{X} ( = \prod_{i \in I} X_i )$ において、すべての $i \in I$ に対して射影 $p_i : \hat{X} \to X_i$ は連続である。
(証明)任意に $x \in \hat{X}$ と $u \in \mathrm{monad}_{\hat{X}}(x)$ をとる。任意に $i \in I $ をとると、【定理1】より $u(i) \in \mathrm{monad}_{X_i}(x(i))$ である。一方、
\begin{equation*}
\forall z \in \hat{X} \, ( p_i(z) = z(i) )
\end{equation*}
と移行原理より、
\begin{equation*}
\forall z \in {}^*\hat{X} \, ( {}^*p_i(z) = z(i) )
\end{equation*}
であるから、${}^*p_i(u) = u(i) \in \mathrm{monad}_{X_i}(x(i)) = \mathrm{monad}_{X_i}(p_i(x))$ となり、第19回【定理2】より $p_i$ は $\hat{X}$ で連続である。□
どの性質も、極めて機械的に証明できることがわかります。
3. カントール空間
本節の議論の応用例として、カントール空間について考察してみます。
自然数の全体 $\mathbb{N}$ から$2$元集合 $\{ \, 0, 1 \, \}$(この集合を $2$ で表します) への写像の全体 ${}^{\mathbb{N}}2 \, ( \, = \prod_{i \in \mathbb{N}} 2 \, )$ を考え、$2$ に離散位相を入れて ${}^{\mathbb{N}}2$ を直積位相空間と考えます。明らかに $2$ はコンパクトだから、【定理4】(チコノフの定理)より ${}^{\mathbb{N}}2$ もコンパクトです。一方、区間 $[ 0, 1 ]$ に属する実数のうち$3$進法無限小数表記で$0$と$2$だけしか現れないようなものの全体 $\mathcal{C}$ は「カントール集合」と呼ばれますが(下図を参照)、これを$1$次元ユークリッド空間 $\mathbb{R}$ の部分位相空間と考えると、$\mathbb{R}$ において有界閉集合なのでこれもコンパクトです。これら ${}^{\mathbb{N}}2$ と $\mathcal{C}$ は実は同相であり、どちらも「カントール空間」と呼ばれる位相空間の一つです。このことを以下で超準的手法を用いて証明します。

図. カントール集合( Wikimedia Commons より)
$x \in {}^{\mathbb{N}}2$ に対し、無限級数 $\displaystyle \sum_{i = 0}^\infty 2 x(i) / 3^{i+1}$ は $\mathbb{R}$ 内で収束するので、その和となる実数値を対応させる写像を $f$ とおくと、$f$ は ${}^{\mathbb{N}}2$ から $\mathcal{C}$ への全単射になります。従ってこの $f$ が連続写像であることを証明すれば、${}^{\mathbb{N}}2$ がコンパクト、$\mathbb{R}$ がハウスドルフ(従って $\mathcal{C}$ もハウスドルフ)なので、第19回【定理6】によって ${}^{\mathbb{N}}2$ と $\mathcal{C}$ が同相であることが示されます。第19回【定理2】を使ってこれを示すのですが、その概略は次のとおりです。
任意に $x \in {}^{\mathbb{N}}2$ をとり、その $x$ に対して任意に $u \in \mathrm{monad}_{{}^{\mathbb{N}}2}(x)$ をとります。$u \in {}^*( {}^{\mathbb{N}}2 )$ なので $u$ は ${}^*\mathbb{N}$ から $2 \, ( ={}^*2 )$ への写像であり、$i \in \mathbb{N}$ に対しては【定理1】より($2$ には離散位相が入るから) $u(i) \in \mathrm{monad}_2(x(i)) = \{ x(i) \}$ なので $u(i) = x(i)$ になります。この $u$ に対する ${}^*f(u)$ は超実数体 ${}^*\mathbb{R}$ における無限級数の和として $\displaystyle {}^*f(u) = {}^*\sum_{i = 0}^\infty 2 u(i) / 3^{i+1}$ となるので、その標準部分は実数体 $\mathbb{R}$ における無限級数の和として
\begin{equation} \tag{3}
\mathrm{st}({}^*f(u)) = \sum_{i = 0}^\infty 2 u(i) / 3^{i+1} = \sum_{i = 0}^\infty 2 x(i) / 3^{i+1} = f(x)
\end{equation}
となります。従って第18回【定理1】より ${}^*f(u) \in \mathrm{monad}_\mathbb{R}(f(x)) \cap {}^*\mathcal{C} = \mathrm{monad}_\mathcal{C}(f(x))$ となるので、第19回【定理2】より $f$ は任意の $x \in {}^{\mathbb{N}}2$ で連続となり、証明が完了します。
この概略の最後の部分(「超実数体 ${}^*\mathbb{R}$ における無限級数の和」以降)は少々直感的にすぎるので、もう少し精密に考えてみます。$z \in {}^{\mathbb{N}}2$ に対する無限級数 $\displaystyle \sum_{i = 0}^\infty 2 z(i) / 3^{i+1}$ は常に $f(z)$ に収束するので、
\begin{equation} \tag{4}
\forall z \in {}^{\mathbb{N}}2 \, \forall \epsilon \in \mathbb{R}^+ \, \exists n \in \mathbb{N} \, \forall k \in \mathbb{N} \, ( k \ge n \to \left| f(z) - \sum_{i = 0}^k 2 z(i) / 3^{i+1} \right| < \epsilon)
\end{equation}
が成り立ちます( $\mathbb{R}^+$ は正実数の全体)。すると移行原理によって、
\begin{equation} \tag{5}
\forall z \in {}^*( {}^{\mathbb{N}}2 ) \, \forall \epsilon \in {}^*\mathbb{R}^+ \, \exists n \in {}^*\mathbb{N} \, \forall k \in {}^*\mathbb{N} \, ( k \ge n \to \left| {}^*f(z) - {}^*\sum_{i = 0}^k 2 z(i) / 3^{i+1} \right| < \epsilon)
\end{equation}
が成り立ちます。そこで $u \in {}^*( {}^{\mathbb{N}}2 )$ に対して任意に正実数 $\epsilon$ をとり、$\mathbb{R}$ における無限級数 $\displaystyle \sum_{i = 0}^\infty 2 u(i) / 3^{i+1}$ の和を $s$ とおくと、$(4)$より十分大きな自然数 $m$ をとると、
\begin{equation*}
\left| s - \sum_{i = 0}^m 2 u(i) / 3^{i+1} \right| < \epsilon
\end{equation*}
が成り立ち、また$(5)$より十分大きな超自然数 $n ( > m)$ をとると、
\begin{equation*}
\left| {}^*f(u) - {}^*\sum_{i = 0}^n 2 u(i) / 3^{i+1} \right| < \epsilon
\end{equation*}
が成り立ちます。そして、
\begin{eqnarray*}
\left| {}^*\sum_{i = 0}^n 2 u(i) / 3^{i+1} - \sum_{i = 0}^m 2 u(i) / 3^{i+1} \right| &=& {}^*\sum_{i = m + 1}^n 2 u(i) / 3^{i+1} \le {}^*\sum_{i = m + 1}^n 2 / 3^{i+1} = \frac{1}{3^{m+1}}-\frac{1}{3^{n+1}} \\
&<& \frac{1}{3^{m+1}}
\end{eqnarray*}
であることから、$m$ を十分大きくとると、
\begin{equation*}
\left| {}^*\sum_{i = 0}^n 2 u(i) / 3^{i+1} - \sum_{i = 0}^m 2 u(i) / 3^{i+1} \right| < \epsilon
\end{equation*}
となるようにできます。これらより、
\begin{eqnarray*}
&&\left| {}^*f(u) - s \right| \\
&\le& \left| {}^*f(u) - {}^*\sum_{i = 0}^n 2 u(i) / 3^{i+1} \right| + \left| {}^*\sum_{i = 0}^n 2 u(i) / 3^{i+1} - \sum_{i = 0}^m 2 u(i) / 3^{i+1} \right| + \left| \sum_{i = 0}^m 2 u(i) / 3^{i+1} -s \right| \\
&<& 3 \epsilon
\end{eqnarray*}
となり、$\epsilon \in \mathbb{R}^+$ は任意なので $\left| {}^*f(u) - s \right| \approx 0$ すなわち $\mathrm{st}({}^*f(u)) = s$ が成り立ちます。これで証明中の($3$)の最初の等号部分が厳密に示されました。
以上で、少し回りくどかったですが、超準的手法を用いて2種類のカントール空間 ${}^{\mathbb{N}}2$ と $\mathcal{C}$ が同相であることを示すことができました。
注意すべきは、「 ${}^{\mathbb{N}}2$ の元は $0$ または $1$ の無限列なので、2進法の無限小数と対応するから、${}^{\mathbb{N}}2$ と実数の区間 $[ 0, 1 ]$ が同相になるのではないのか?」と早とちりしてはいけないということです。$x \in {}^{\mathbb{N}}2$ に無限級数 $\displaystyle \sum_{i = 0}^\infty x(i) / 2^{i+1}$ を対応させると、例えば2進法無限小数 $0.011111 \cdots$ は $0.100000 \cdots$ と実数として等しいので、この対応では ${}^{\mathbb{N}}2$ と $[ 0, 1 ]$ が1対1になりません。一方、先ほどの証明の方法で ${}^{\mathbb{N}}2$ の元に3進法無限小数を対応させると、例えば $0.022222 \cdots = 0.100000 \cdots$ ですが、後者は $1$ を含むので ${}^{\mathbb{N}}2$ の元に対応せず、従ってこちらの対応だと ${}^{\mathbb{N}}2$ と $\mathcal{C}$ が1対1になるのです。
(続く)(前記事)(目次)
わかってない奴がわかったつもりで書き留める超準解析(その19) [数学]
【超準解析について生半可な知識しかない僕が、わかったつもりの内容をちょっとずつ書き留めていきます。不正確な内容や誤りもあることをご承知ください。】
(19) 位相空間の連続写像
位相空間における写像(関数)の連続性についても、超準解析を使ったわかりやすい同値条件があります。本記事ではそのことを示し、それを用いて幾つかの定理を証明します。
1. 準備
本題に入る前に、直積や写像を超準解析で扱う際の基本事項について確認しておきます。
2つの集合 $X,Y$ があるとき、それらの直積 $X \times Y$ について、
\begin{equation*}
\forall x \in X \, \land y \in Y \, ( \langle x, y \rangle \in X \times Y )
\end{equation*}
が成り立ち、移行原理より、
\begin{equation*}
\forall x \in {}^*X \, \land y \in {}^*Y \, ( \langle x, y \rangle \in {}^*( X \times Y ) )
\end{equation*}
となるので ${}^*X \times {}^*Y \subseteq {}^*( X \times Y )$ です。一方、
\begin{equation*}
\forall z \in X \times Y \, ( \exists x \in X \, \exists y \in Y \, ( z = \langle x, y \rangle ) )
\end{equation*}
が成り立ち、移行原理より、
\begin{equation*}
\forall z \in {}^*( X \times Y ) \, ( \exists x \in {}^*X \, \exists y \in {}^*Y \, ( z = \langle x, y \rangle ) )
\end{equation*}
となるので ${}^*( X \times Y ) \subseteq {}^*X \times {}^*Y$ であり、あわせて
\begin{equation} \tag{1}
{}^*(X \times Y) = {}^*X \times {}^*Y
\end{equation}
が成立します。
また、$f$ が $X$ から $Y$ への写像であるとは、
\begin{equation} \tag{2}
\forall z \in f \, \exists x \in X \, \exists y \in Y \, ( z = \langle x, y \rangle ) \land \forall x \in X \, \exists ! y \in Y \, ( \langle x, y \rangle \in f )
\end{equation}
が成り立つことをいいます。このとき移行原理より、
\begin{equation*}
\forall z \in {}^*f \, \exists x \in {}^*X \, \exists y \in {}^*Y \, ( z = \langle x, y \rangle ) \land \forall x \in {}^*X \, \exists ! y \in {}^*Y \, ( \langle x, y \rangle \in {}^*f )
\end{equation*}
が成り立つので、$(2)$に照らし合わせることにより ${}^*f$ は ${}^*X$ から ${}^*Y$ への写像となります。$f \subseteq {}^*f$ なので、$x \in X$ のときは ${}^*f(x) = f(x)$ です。
写像の超準拡大については次が成立します( $A \subseteq X, B \subseteq Y$ とします)。
i) 像について ${}^*(f[A]) = {}^*f[{}^*A]$
ii) 逆像について ${}^*(f^{-1}[B]) = {}^*f^{-1}[{}^*B]$
iii) 制限について ${}^*(f \upharpoonright A) = {}^*f \upharpoonright {}^*A$
iv) $f$ が全単射ならば ${}^*f$ も全単射で、逆写像について ${}^*(f^{-1}) = {}^*f^{-1}$
これらは移行原理から簡単に導かれるので証明は省略し、以下自由に用いることにします。
ここから位相空間の内容に入ります。$X, Y$ がそれぞれ開集合族 $\mathcal{O}_X, \mathcal{O}_Y$ によって位相空間となっているとすると、直積 $X \times Y$ の部分集合の族
\begin{equation*}
\{ \, U \times V \, \mid \, U \in \mathcal{O}_X \land V \in \mathcal{O}_Y \, \}
\end{equation*}
は $X \times Y$ の開基の条件を満たすので、これによって $X \times Y$ の位相(直積位相)が定まります。このとき、モナドについて次が成立します。
ここで位相空間 $X$ の点 $x$ のモナドは、$\mathcal{N}_X(x)$ を $x$ の近傍の全体として、
\begin{equation*}
\mathrm{monad}_X(x) = \bigcap \{ \, {}^*A \, \mid \, A \in \mathcal{N}_X(x) \, \}
\end{equation*}
によって定まることを思い出しましょう。本記事ではいくつもの異なった位相空間が登場するので、どの空間についてのモナドや近傍なのかを表す添字は省略しません。
(証明)任意に $A \in \mathcal{N}_X(x)$ と $B \in \mathcal{N}_Y(y)$ をとると、ある $x$ の開近傍 $U$ と $y$ の開近傍 $V$ で $U \subseteq A \land V \subseteq B$ となるものが存在するから、$U \times V \subseteq A \times B$ と直積位相の定義より $A \times B \in \mathcal{N}_{X \times Y}( \langle x, y \rangle )$ である。よって$(1)$より
\begin{equation*}
\mathrm{monad}_{X \times Y}( \langle x, y \rangle ) \subseteq {}^*(A \times B) = {}^*A \times {}^*B
\end{equation*}
であり、$A, B$ は任意だから、
\begin{equation*}
\mathrm{monad}_{X \times Y}( \langle x, y \rangle ) \subseteq \mathrm{monad}_X(x) \times \mathrm{monad}_Y(y)
\end{equation*}
が成り立つ。
逆に、任意に $C \in \mathcal{N}_{X \times Y}( \langle x, y \rangle )$ をとると、ある $\langle x, y \rangle$ の開近傍 $W$ で $W \subseteq C$ となるものが存在し、直積位相の定義より $x$ の開近傍 $U$ と $y$ の開近傍 $V$ で $U \times V \subseteq W \subseteq C$ となるものが存在するから、$(1)$より
\begin{equation*}
\mathrm{monad}_X(x) \times \mathrm{monad}_Y(y) \subseteq {}^*U \times {}^*V = {}^*(U \times V) \subseteq {}^*C
\end{equation*}
である。$C$ は任意だから、
\begin{equation*}
\mathrm{monad}_X(x) \times \mathrm{monad}_Y(y) \subseteq \mathrm{monad}_{X \times Y}( \langle x, y \rangle )
\end{equation*}
が成り立つ。□
2. 連続写像に関する定理
以上を踏まえて、本題の位相空間の連続性に入ります。位相空間 $X$ から位相空間 $Y$ への写像 $f$ が $X$ の点 $x$ で連続であるとは、$Y$ における点 $f(x)$ の任意の近傍 $B$ に対し、その逆像 $f^{-1}[B]$ が $X$ における $x$ の近傍となることをいいます。記号で書くと次のとおりです。
\begin{equation} \tag{3}
\forall B \in \mathcal{N}_Y(f(x)) \, ( f^{-1}[B] \in \mathcal{N}_X(x) )
\end{equation}
これは超準モデルを使って次の同値な条件で表すことができます。今回の主題となる定理です。
(証明)$(3) \Leftrightarrow (4)$ を示せばよい。
$(3) \Rightarrow (4)$:$(3)$が成り立つとし、$(4)$が成り立たないと仮定して矛盾を導く。このとき ${}^*f(u) \notin \mathrm{monad}_Y(f(x))$ となる $u \in \mathrm{monad}_X(x)$ が存在し、この $u$ に対してある $B \in \mathcal{N}_Y(f(x))$ で ${}^*f(u) \notin {}^*B$ となるものが存在するが、$(3)$より $f^{-1}[B] \in \mathcal{N}_X(x)$ であるから、$\mathrm{monad}_X(x) \subseteq {}^*(f^{-1}[B]) = {}^*f^{-1}[{}^*B]$ となって、$u \in {}^*f^{-1}[{}^*B]$ である。これは ${}^*f(u) \in {}^*B$ を意味するから矛盾である。
$(3) \Leftarrow (4)$:$(4)$が成り立つとし、$(3)$が成り立たないと仮定して矛盾を導く。このとき $f^{-1}[B] \notin \mathcal{N}_X(x)$ となる $B \in \mathcal{N}_Y(f(x))$ が存在する。この $B$ に対して $\mathrm{monad}_X(x) \not\subseteq {}^*(f^{-1}[B]) = {}^*f^{-1}[{}^*B]$ であるから、$u \in \mathrm{monad}_X(x) \setminus {}^*f^{-1}[{}^*B]$ となる $u$ をとると、$(4)$より ${}^*f(u) \in \mathrm{monad}_Y(f(x))$ であるが、一方で $u \notin {}^*f^{-1}[{}^*B]$ より ${}^*f(u) \notin {}^*B$ であるから $\mathrm{monad}_Y(f(x)) \not\subseteq {}^*B$ である。これは $B \in \mathcal{N}_Y(f(x))$ と矛盾する。□
以下、これを使って連続写像に関する諸定理を超準的手法で証明します。「開集合の逆像は開集合」は定義よりほとんど自明なので省略します。「閉集合の逆像は閉集合」も補集合を使えばそこからすぐに導かれますが、次のように超準的手法で証明することもできます。
(証明)任意に $\mathrm{monad}_X(x) \cap {}^*(f^{-1}[B]) \neq \emptyset$ となる $x \in X$ をとる。このとき $u \in \mathrm{monad}_X(x) \cap {}^*(f^{-1}[B])$ となる $u$ が存在し、$f$ は $x$ で連続だから【定理2】より ${}^*f(u) \in \mathrm{monad}_Y(f(x))$ であり、また $u \in {}^*(f^{-1}[B]) = {}^*f^{-1}[{}^*B]$ だから ${}^*f(u) \in {}^*B$ であり、これらより $\mathrm{monad}_Y(f(x)) \cap {}^*B \neq \emptyset$ である。$B$ は閉集合だから第17回【定理3】 ii) より $f(x) \in B$ であり、よって $x \in f^{-1}[B]$ だから、再び第17回【定理3】 ii) より $f^{-1}[B]$ は閉集合である。□
「連結集合の像は連結集合」はこれらから容易に導かれるので省略します。
次にコンパクト性に関する定理を証明します。
(証明)
i) 任意に $v \in {}^*(f[A])$ をとる。$v \in {}^*f[{}^*A]$ だから、ある $u \in {}^*A$ に対して ${}^*f(u) = v$ となる。$A$ はコンパクトだから、第17回【定理5】より $u \in \mathrm{monad}_X(x)$ となる $x \in A$ が存在する。$f$ は $x$ で連続だから、【定理2】より
\begin{equation*}
v = {}^*f(u) \in \mathrm{monad}_Y(f(x))
\end{equation*}
である。$f(x) \in f[A]$ だから、第17回【定理5】より $f[A]$ はコンパクトである。
ii) 任意に $\langle u, v \rangle \in {}^*(f \upharpoonright A)$ をとる。$\langle u, v \rangle \in {}^*f \upharpoonright {}^*A$ だから $u \in {}^*A$ で、$A$ がコンパクトだから第17回【定理5】より $u \in \mathrm{monad}_X(x)$ となる $x \in A$ が存在する。$f$ は $x$ で連続だから【定理2】より $v = {}^*f(u) \in \mathrm{monad}_Y(f(x))$ であり、【補題1】より
\begin{equation*}
\langle u, v \rangle \in \mathrm{monad}_X(x) \times \mathrm{monad}_Y(f(x)) = \mathrm{monad}_{X \times Y}( \langle x, f(x) \rangle )
\end{equation*}
である。$\langle x, f(x) \rangle \in f \upharpoonright A$ だから第17回【定理5】より $f \upharpoonright A$ はコンパクトである。□
次に、【定理4】 ii) のある意味逆といえる定理を証明します。
(証明)任意に $x \in X$ と $u \in \mathrm{monad}_X(x)$ をとる。このとき $\langle u, {}^*f(u) \rangle \in {}^*f$ で、$f$ は $X \times Y$ 上でコンパクトだから、第17回【定理5】より $\langle u, {}^*f(u) \rangle \in \mathrm{monad}_{X \times Y}( \langle x', f(x') \rangle )$ となる $x' \in X$ が存在する。【補題1】より $\mathrm{monad}_{X \times Y}( \langle x', f(x') \rangle ) = \mathrm{monad}_X(x') \times \mathrm{monad}_Y(f(x'))$ だから、$u \in \mathrm{monad}_X(x')$ かつ ${}^*f(u) \in \mathrm{monad}_Y(f(x'))$ である。これらより $\mathrm{monad}_X(x) \cap \mathrm{monad}_X(x') \neq \emptyset$ であり、$X$ はハウスドルフだから第17回【定理4】 ii) より $x = x'$ が従う。よって ${}^*f(u) \in \mathrm{monad}_Y(f(x))$ となり、【定理2】より $f$ は $x$ で連続であり、従って $X$ で連続である。□
この定理から、2つの位相空間が同相になるための一つの十分条件が示されます。
(証明)$f$ が全単射だから逆写像 $f^{-1}$ が存在し、これが $Y \times X$ 上でコンパクトであることを示す。任意に $\langle v, u \rangle \in {}^*(f^{-1})$ をとると、${}^*(f^{-1}) = {}^*f^{-1} \subseteq {}^*Y \times {}^*X$ より $u \in {}^*X$ であり、$X$ がコンパクトだから第17回【定理5】より $u \in \mathrm{monad}_X(x)$ となる $x \in X$ が存在する。$f$ は $x$ で連続だから、【定理2】より $v = {}^*f(u) \in \mathrm{monad}_Y(f(x))$ である。よって【補題1】より、
\begin{equation*}
\langle v, u \rangle \in \mathrm{monad}_Y(f(x)) \times \mathrm{monad}_X(x) = \mathrm{monad}_{Y \times X}( \langle f(x), x \rangle )
\end{equation*}
かつ $\langle f(x), x \rangle \in f^{-1}$ だから、第17回【定理5】より $f^{-1}$ はコンパクトである。すると、$Y$ がハウスドルフだから【定理5】より $f^{-1}$ は $Y$ で連続である。従って $X$ と $Y$ は同相であり、任意の $x \in X$ に対し、$(4)$を $f^{-1}$ に適用して ${}^*f^{-1}[ \mathrm{monad}_Y(f(x)) ] \subseteq \mathrm{monad}_X(x)$ となるから $\mathrm{monad}_Y(f(x)) \subseteq {}^*f[ \mathrm{monad}_X(x) ]$ であり、これと$(4)$より ${}^*f[ \mathrm{monad}_X(x) ] = \mathrm{monad}_Y(f(x))$ が得られ、$x \in X$ は任意だから$(5)$が得られる。□
このように、いろんな定理が超準的手法の条件の組み合わせで機械的に証明できることがわかります。
3. ユークリッド空間への応用
ここで応用例として、2次元以上のユークリッド空間が1次元ユークリッド空間と同相にならないことを、超準的手法を用いて証明することとします。まずそれに用いる常識的な補題から。
(証明)任意に $x \in X$ と $u \in \mathrm{monad}_X(x)$ をとる。【補題1】より、
\begin{equation*}
\langle u, y_0 \rangle \in \mathrm{monad}_X(x) \times \mathrm{monad}_Y(y_0) = \mathrm{monad}_{X \times Y}( \langle x, y_0 \rangle )
\end{equation*}
であり、$f$ は連続だから【定理2】より
\begin{equation*}
{}^*g(u) = {}^*f( \langle u, y_0 \rangle ) \in \mathrm{monad}_Z( f( \langle x, y_0 \rangle ) ) = \mathrm{monad}_Z( g(x) )
\end{equation*}
である。従って再び【定理2】より $g$ は連続である。□
次が証明したい事柄です。
(証明)$\mathbb{R}$ のユークリッド位相における「連結であることと区間であることは同値」「有界閉区間はコンパクト」という事実を用いる。
内点をもつ $\mathbb{R}^n$ の部分集合を $C$ とし、$C$ から $\mathbb{R}$ への連続な単射 $f$ が存在すると仮定して矛盾を導く。以下 $m = n - 1$ とおいて $\mathbb{R}^n = \mathbb{R} \times \mathbb{R}^m$ とみなし、また $\langle x,y \rangle \in \mathbb{R} \times \mathbb{R}^m$ に対して $f( \langle x,y \rangle )$ を $f(x,y)$ とかく。
$C$ の内点 $\langle a, b \rangle \ ( a \in \mathbb{R} \land b \in \mathbb{R}^m )$ をとり、$a$ を内点にもつ $\mathbb{R}$ の閉区間 $A$ と、$\mathbb{R}^m$ における $b$ の近傍 $B$ を、$A \times B \subseteq C$ となるようにとる($A, B$ を十分小さくとれば可能)。
$A$ から $\mathbb{R}$ への写像 $g$ を $g(x) = f(x,b)$ によって定めると、$f$ が $A \times B$ で連続な単射だから、【補題7】より $g$ も $A$ で連続な単射である。$A$ はコンパクトで $\mathbb{R}$ はハウスドルフだから、【定理6】より
\begin{equation} \tag{6}
\forall x \in A \, ( {}^*g[ \mathrm{monad}_A(x) ] = \mathrm{monad}_{g[A]}(f(x)) )
\end{equation}
が成立する。また $A$ は $\mathbb{R}$ の区間だから連結で、その連続写像 $g$ による像 $g[A]$ も連結だから $\mathbb{R}$ の区間である。$A$ は2点以上をもち $g$ は単射だから $g[A]$ も2点以上をもち、従って内点 $c$ がとれる。この $c$ に対し $\mathrm{monad}_{\mathbb{R}}(c) \subseteq {}^*(g[A])$ であり、よって
\begin{equation*}
\mathrm{monad}_{g[A]}(c) = \mathrm{monad}_{\mathbb{R}}(c) \cap {}^*(g[A]) = \mathrm{monad}_{\mathbb{R}}(c)
\end{equation*}
である。$f(a') = c$ となる $a' \in A$ をとると、$(6)$より
\begin{equation} \tag{7}
{}^*g[ \mathrm{monad}_A(a') ] = \mathrm{monad}_{g[A]}(c) = \mathrm{monad}_{\mathbb{R}}(c)
\end{equation}
が成り立つ。
この $a'$ に対し、$B$ から $\mathbb{R}$ への写像 $h$ を $h(y) = f(a',y)$ によって定める。$b$ は $\mathbb{R}^m$ の位相における $B$ の内点だから $\mathrm{monad}_{\mathbb{R}^m}(b) \subseteq {}^*B$ であり、よって
\begin{equation*}
\mathrm{monad}_B(b) = \mathrm{monad}_{\mathbb{R}^m}(b) \cap {}^*B = \mathrm{monad}_{\mathbb{R}^m}(b)
\end{equation*}
であるから、$v \neq b$ となる $v \in \mathrm{monad}_B(b)$ がとれる。【補題7】より $h$ も $B$ で連続だから、【定理2】より ${}^*h(v) \in \mathrm{monad}_{h[B]}(c) \subseteq \mathrm{monad}_{\mathbb{R}}(c)$ である。$(7)$より ${}^*g(u) = {}^*h(v)$ となる $u \in \mathrm{monad}_A(a')$ がとれ、${}^*f(u,b) = {}^*g(u)$ かつ ${}^*f(a',v) = {}^*h(v)$ より ${}^*f(u,b) = {}^*f(a',v)$ が得られるが、$f$ は単射だから ${}^*f$ も単射であり、$\langle u, b \rangle \neq \langle a', v \rangle$ だからこれは矛盾である。□
直線と平面が同じ濃度を持つことを発見したカントルがその事実に困惑したのを見て、デデキントがカントルを慰める?ために指摘した内容を、ここでは超準解析を用いて証明してみました。
(続く)(前記事)(目次)
(19) 位相空間の連続写像
位相空間における写像(関数)の連続性についても、超準解析を使ったわかりやすい同値条件があります。本記事ではそのことを示し、それを用いて幾つかの定理を証明します。
1. 準備
本題に入る前に、直積や写像を超準解析で扱う際の基本事項について確認しておきます。
2つの集合 $X,Y$ があるとき、それらの直積 $X \times Y$ について、
\begin{equation*}
\forall x \in X \, \land y \in Y \, ( \langle x, y \rangle \in X \times Y )
\end{equation*}
が成り立ち、移行原理より、
\begin{equation*}
\forall x \in {}^*X \, \land y \in {}^*Y \, ( \langle x, y \rangle \in {}^*( X \times Y ) )
\end{equation*}
となるので ${}^*X \times {}^*Y \subseteq {}^*( X \times Y )$ です。一方、
\begin{equation*}
\forall z \in X \times Y \, ( \exists x \in X \, \exists y \in Y \, ( z = \langle x, y \rangle ) )
\end{equation*}
が成り立ち、移行原理より、
\begin{equation*}
\forall z \in {}^*( X \times Y ) \, ( \exists x \in {}^*X \, \exists y \in {}^*Y \, ( z = \langle x, y \rangle ) )
\end{equation*}
となるので ${}^*( X \times Y ) \subseteq {}^*X \times {}^*Y$ であり、あわせて
\begin{equation} \tag{1}
{}^*(X \times Y) = {}^*X \times {}^*Y
\end{equation}
が成立します。
また、$f$ が $X$ から $Y$ への写像であるとは、
\begin{equation} \tag{2}
\forall z \in f \, \exists x \in X \, \exists y \in Y \, ( z = \langle x, y \rangle ) \land \forall x \in X \, \exists ! y \in Y \, ( \langle x, y \rangle \in f )
\end{equation}
が成り立つことをいいます。このとき移行原理より、
\begin{equation*}
\forall z \in {}^*f \, \exists x \in {}^*X \, \exists y \in {}^*Y \, ( z = \langle x, y \rangle ) \land \forall x \in {}^*X \, \exists ! y \in {}^*Y \, ( \langle x, y \rangle \in {}^*f )
\end{equation*}
が成り立つので、$(2)$に照らし合わせることにより ${}^*f$ は ${}^*X$ から ${}^*Y$ への写像となります。$f \subseteq {}^*f$ なので、$x \in X$ のときは ${}^*f(x) = f(x)$ です。
写像の超準拡大については次が成立します( $A \subseteq X, B \subseteq Y$ とします)。
i) 像について ${}^*(f[A]) = {}^*f[{}^*A]$
ii) 逆像について ${}^*(f^{-1}[B]) = {}^*f^{-1}[{}^*B]$
iii) 制限について ${}^*(f \upharpoonright A) = {}^*f \upharpoonright {}^*A$
iv) $f$ が全単射ならば ${}^*f$ も全単射で、逆写像について ${}^*(f^{-1}) = {}^*f^{-1}$
これらは移行原理から簡単に導かれるので証明は省略し、以下自由に用いることにします。
ここから位相空間の内容に入ります。$X, Y$ がそれぞれ開集合族 $\mathcal{O}_X, \mathcal{O}_Y$ によって位相空間となっているとすると、直積 $X \times Y$ の部分集合の族
\begin{equation*}
\{ \, U \times V \, \mid \, U \in \mathcal{O}_X \land V \in \mathcal{O}_Y \, \}
\end{equation*}
は $X \times Y$ の開基の条件を満たすので、これによって $X \times Y$ の位相(直積位相)が定まります。このとき、モナドについて次が成立します。
【補題1】位相空間 $X, Y$ と直積位相空間 $X \times Y$ および任意の $x \in X, \, y \in Y$ に対して、次が成立する。
\begin{equation*}
\mathrm{monad}_{X \times Y}( \langle x, y \rangle ) = \mathrm{monad}_X(x) \times \mathrm{monad}_Y(y)
\end{equation*}
ここで位相空間 $X$ の点 $x$ のモナドは、$\mathcal{N}_X(x)$ を $x$ の近傍の全体として、
\begin{equation*}
\mathrm{monad}_X(x) = \bigcap \{ \, {}^*A \, \mid \, A \in \mathcal{N}_X(x) \, \}
\end{equation*}
によって定まることを思い出しましょう。本記事ではいくつもの異なった位相空間が登場するので、どの空間についてのモナドや近傍なのかを表す添字は省略しません。
(証明)任意に $A \in \mathcal{N}_X(x)$ と $B \in \mathcal{N}_Y(y)$ をとると、ある $x$ の開近傍 $U$ と $y$ の開近傍 $V$ で $U \subseteq A \land V \subseteq B$ となるものが存在するから、$U \times V \subseteq A \times B$ と直積位相の定義より $A \times B \in \mathcal{N}_{X \times Y}( \langle x, y \rangle )$ である。よって$(1)$より
\begin{equation*}
\mathrm{monad}_{X \times Y}( \langle x, y \rangle ) \subseteq {}^*(A \times B) = {}^*A \times {}^*B
\end{equation*}
であり、$A, B$ は任意だから、
\begin{equation*}
\mathrm{monad}_{X \times Y}( \langle x, y \rangle ) \subseteq \mathrm{monad}_X(x) \times \mathrm{monad}_Y(y)
\end{equation*}
が成り立つ。
逆に、任意に $C \in \mathcal{N}_{X \times Y}( \langle x, y \rangle )$ をとると、ある $\langle x, y \rangle$ の開近傍 $W$ で $W \subseteq C$ となるものが存在し、直積位相の定義より $x$ の開近傍 $U$ と $y$ の開近傍 $V$ で $U \times V \subseteq W \subseteq C$ となるものが存在するから、$(1)$より
\begin{equation*}
\mathrm{monad}_X(x) \times \mathrm{monad}_Y(y) \subseteq {}^*U \times {}^*V = {}^*(U \times V) \subseteq {}^*C
\end{equation*}
である。$C$ は任意だから、
\begin{equation*}
\mathrm{monad}_X(x) \times \mathrm{monad}_Y(y) \subseteq \mathrm{monad}_{X \times Y}( \langle x, y \rangle )
\end{equation*}
が成り立つ。□
2. 連続写像に関する定理
以上を踏まえて、本題の位相空間の連続性に入ります。位相空間 $X$ から位相空間 $Y$ への写像 $f$ が $X$ の点 $x$ で連続であるとは、$Y$ における点 $f(x)$ の任意の近傍 $B$ に対し、その逆像 $f^{-1}[B]$ が $X$ における $x$ の近傍となることをいいます。記号で書くと次のとおりです。
\begin{equation} \tag{3}
\forall B \in \mathcal{N}_Y(f(x)) \, ( f^{-1}[B] \in \mathcal{N}_X(x) )
\end{equation}
これは超準モデルを使って次の同値な条件で表すことができます。今回の主題となる定理です。
【定理2】位相空間 $X$ から位相空間 $Y$ への写像 $f$ が $X$ の点 $x$ で連続であることと、
\begin{equation*}
\forall u \in \mathrm{monad}_X(x) \, ({}^*f(u) \in \mathrm{monad}_Y(f(x)) )
\end{equation*}
すなわち
\begin{equation} \tag{4}
{}^*f[ \mathrm{monad}_X(x) ] \subseteq \mathrm{monad}_Y(f(x))
\end{equation}
が成り立つことは同値である。
(証明)$(3) \Leftrightarrow (4)$ を示せばよい。
$(3) \Rightarrow (4)$:$(3)$が成り立つとし、$(4)$が成り立たないと仮定して矛盾を導く。このとき ${}^*f(u) \notin \mathrm{monad}_Y(f(x))$ となる $u \in \mathrm{monad}_X(x)$ が存在し、この $u$ に対してある $B \in \mathcal{N}_Y(f(x))$ で ${}^*f(u) \notin {}^*B$ となるものが存在するが、$(3)$より $f^{-1}[B] \in \mathcal{N}_X(x)$ であるから、$\mathrm{monad}_X(x) \subseteq {}^*(f^{-1}[B]) = {}^*f^{-1}[{}^*B]$ となって、$u \in {}^*f^{-1}[{}^*B]$ である。これは ${}^*f(u) \in {}^*B$ を意味するから矛盾である。
$(3) \Leftarrow (4)$:$(4)$が成り立つとし、$(3)$が成り立たないと仮定して矛盾を導く。このとき $f^{-1}[B] \notin \mathcal{N}_X(x)$ となる $B \in \mathcal{N}_Y(f(x))$ が存在する。この $B$ に対して $\mathrm{monad}_X(x) \not\subseteq {}^*(f^{-1}[B]) = {}^*f^{-1}[{}^*B]$ であるから、$u \in \mathrm{monad}_X(x) \setminus {}^*f^{-1}[{}^*B]$ となる $u$ をとると、$(4)$より ${}^*f(u) \in \mathrm{monad}_Y(f(x))$ であるが、一方で $u \notin {}^*f^{-1}[{}^*B]$ より ${}^*f(u) \notin {}^*B$ であるから $\mathrm{monad}_Y(f(x)) \not\subseteq {}^*B$ である。これは $B \in \mathcal{N}_Y(f(x))$ と矛盾する。□
以下、これを使って連続写像に関する諸定理を超準的手法で証明します。「開集合の逆像は開集合」は定義よりほとんど自明なので省略します。「閉集合の逆像は閉集合」も補集合を使えばそこからすぐに導かれますが、次のように超準的手法で証明することもできます。
【定理3】$X, Y$ は位相空間、$f$ は $X$ から $Y$ への写像で $X$(上のすべての点)で連続とする。$B \in \mathscr{P}(Y)$ が閉集合ならば、逆像 $f^{-1}[B]$ は閉集合である。
(証明)任意に $\mathrm{monad}_X(x) \cap {}^*(f^{-1}[B]) \neq \emptyset$ となる $x \in X$ をとる。このとき $u \in \mathrm{monad}_X(x) \cap {}^*(f^{-1}[B])$ となる $u$ が存在し、$f$ は $x$ で連続だから【定理2】より ${}^*f(u) \in \mathrm{monad}_Y(f(x))$ であり、また $u \in {}^*(f^{-1}[B]) = {}^*f^{-1}[{}^*B]$ だから ${}^*f(u) \in {}^*B$ であり、これらより $\mathrm{monad}_Y(f(x)) \cap {}^*B \neq \emptyset$ である。$B$ は閉集合だから第17回【定理3】 ii) より $f(x) \in B$ であり、よって $x \in f^{-1}[B]$ だから、再び第17回【定理3】 ii) より $f^{-1}[B]$ は閉集合である。□
「連結集合の像は連結集合」はこれらから容易に導かれるので省略します。
次にコンパクト性に関する定理を証明します。
【定理4】$X, Y$ は位相空間、$A \in \mathscr{P}(X)$ は $X$ 上でコンパクト、$f$ は $X$ から $Y$ への写像で $A$ で連続とすると、次が成立する。
i) 像 $f[A]$ は $Y$ 上でコンパクトである。
ii) 制限 $f \upharpoonright A$(のグラフ)は $X \times Y$ 上でコンパクトである。
i) 像 $f[A]$ は $Y$ 上でコンパクトである。
ii) 制限 $f \upharpoonright A$(のグラフ)は $X \times Y$ 上でコンパクトである。
(証明)
i) 任意に $v \in {}^*(f[A])$ をとる。$v \in {}^*f[{}^*A]$ だから、ある $u \in {}^*A$ に対して ${}^*f(u) = v$ となる。$A$ はコンパクトだから、第17回【定理5】より $u \in \mathrm{monad}_X(x)$ となる $x \in A$ が存在する。$f$ は $x$ で連続だから、【定理2】より
\begin{equation*}
v = {}^*f(u) \in \mathrm{monad}_Y(f(x))
\end{equation*}
である。$f(x) \in f[A]$ だから、第17回【定理5】より $f[A]$ はコンパクトである。
ii) 任意に $\langle u, v \rangle \in {}^*(f \upharpoonright A)$ をとる。$\langle u, v \rangle \in {}^*f \upharpoonright {}^*A$ だから $u \in {}^*A$ で、$A$ がコンパクトだから第17回【定理5】より $u \in \mathrm{monad}_X(x)$ となる $x \in A$ が存在する。$f$ は $x$ で連続だから【定理2】より $v = {}^*f(u) \in \mathrm{monad}_Y(f(x))$ であり、【補題1】より
\begin{equation*}
\langle u, v \rangle \in \mathrm{monad}_X(x) \times \mathrm{monad}_Y(f(x)) = \mathrm{monad}_{X \times Y}( \langle x, f(x) \rangle )
\end{equation*}
である。$\langle x, f(x) \rangle \in f \upharpoonright A$ だから第17回【定理5】より $f \upharpoonright A$ はコンパクトである。□
次に、【定理4】 ii) のある意味逆といえる定理を証明します。
【定理5】$X, Y$ は位相空間で $X$ はハウスドルフとするとき、$X$ から $Y$ への写像 $f$ が $X \times Y$ 上でコンパクトならば、$f$ は $X$ で連続である。
(証明)任意に $x \in X$ と $u \in \mathrm{monad}_X(x)$ をとる。このとき $\langle u, {}^*f(u) \rangle \in {}^*f$ で、$f$ は $X \times Y$ 上でコンパクトだから、第17回【定理5】より $\langle u, {}^*f(u) \rangle \in \mathrm{monad}_{X \times Y}( \langle x', f(x') \rangle )$ となる $x' \in X$ が存在する。【補題1】より $\mathrm{monad}_{X \times Y}( \langle x', f(x') \rangle ) = \mathrm{monad}_X(x') \times \mathrm{monad}_Y(f(x'))$ だから、$u \in \mathrm{monad}_X(x')$ かつ ${}^*f(u) \in \mathrm{monad}_Y(f(x'))$ である。これらより $\mathrm{monad}_X(x) \cap \mathrm{monad}_X(x') \neq \emptyset$ であり、$X$ はハウスドルフだから第17回【定理4】 ii) より $x = x'$ が従う。よって ${}^*f(u) \in \mathrm{monad}_Y(f(x))$ となり、【定理2】より $f$ は $x$ で連続であり、従って $X$ で連続である。□
この定理から、2つの位相空間が同相になるための一つの十分条件が示されます。
【定理6】$X, Y$ は位相空間、$X$ はコンパクトで $Y$ はハウスドルフ、$f$ は $X$ から $Y$ への連続な全単射とすると、逆写像 $f^{-1}$ も $Y$ で連続である。従って $X$ と $Y$ は同相であり、
\begin{equation} \tag{5}
\forall x \in X \, ( {}^*f[ \mathrm{monad}_X(x) ] = \mathrm{monad}_Y(f(x)) )
\end{equation}
が成立する。
(証明)$f$ が全単射だから逆写像 $f^{-1}$ が存在し、これが $Y \times X$ 上でコンパクトであることを示す。任意に $\langle v, u \rangle \in {}^*(f^{-1})$ をとると、${}^*(f^{-1}) = {}^*f^{-1} \subseteq {}^*Y \times {}^*X$ より $u \in {}^*X$ であり、$X$ がコンパクトだから第17回【定理5】より $u \in \mathrm{monad}_X(x)$ となる $x \in X$ が存在する。$f$ は $x$ で連続だから、【定理2】より $v = {}^*f(u) \in \mathrm{monad}_Y(f(x))$ である。よって【補題1】より、
\begin{equation*}
\langle v, u \rangle \in \mathrm{monad}_Y(f(x)) \times \mathrm{monad}_X(x) = \mathrm{monad}_{Y \times X}( \langle f(x), x \rangle )
\end{equation*}
かつ $\langle f(x), x \rangle \in f^{-1}$ だから、第17回【定理5】より $f^{-1}$ はコンパクトである。すると、$Y$ がハウスドルフだから【定理5】より $f^{-1}$ は $Y$ で連続である。従って $X$ と $Y$ は同相であり、任意の $x \in X$ に対し、$(4)$を $f^{-1}$ に適用して ${}^*f^{-1}[ \mathrm{monad}_Y(f(x)) ] \subseteq \mathrm{monad}_X(x)$ となるから $\mathrm{monad}_Y(f(x)) \subseteq {}^*f[ \mathrm{monad}_X(x) ]$ であり、これと$(4)$より ${}^*f[ \mathrm{monad}_X(x) ] = \mathrm{monad}_Y(f(x))$ が得られ、$x \in X$ は任意だから$(5)$が得られる。□
このように、いろんな定理が超準的手法の条件の組み合わせで機械的に証明できることがわかります。
3. ユークリッド空間への応用
ここで応用例として、2次元以上のユークリッド空間が1次元ユークリッド空間と同相にならないことを、超準的手法を用いて証明することとします。まずそれに用いる常識的な補題から。
【補題7】$X, Y, Z$ は位相空間、$f$ は $X \times Y$ から $Z$ への連続写像とすると、ある $y_0 \in Y$ に対して
\begin{equation*}
g : X \to Z, \, x \mapsto f(x,y_0)
\end{equation*}
によって定まる写像 $g$ も連続である。
(証明)任意に $x \in X$ と $u \in \mathrm{monad}_X(x)$ をとる。【補題1】より、
\begin{equation*}
\langle u, y_0 \rangle \in \mathrm{monad}_X(x) \times \mathrm{monad}_Y(y_0) = \mathrm{monad}_{X \times Y}( \langle x, y_0 \rangle )
\end{equation*}
であり、$f$ は連続だから【定理2】より
\begin{equation*}
{}^*g(u) = {}^*f( \langle u, y_0 \rangle ) \in \mathrm{monad}_Z( f( \langle x, y_0 \rangle ) ) = \mathrm{monad}_Z( g(x) )
\end{equation*}
である。従って再び【定理2】より $g$ は連続である。□
次が証明したい事柄です。
【定理8】$n \ge 2$ のとき、内点をもつ $\mathbb{R}^n$ の部分集合から $\mathbb{R}$ への連続な単射は存在しない。ただし位相は通常のユークリッド位相とする。
(証明)$\mathbb{R}$ のユークリッド位相における「連結であることと区間であることは同値」「有界閉区間はコンパクト」という事実を用いる。
内点をもつ $\mathbb{R}^n$ の部分集合を $C$ とし、$C$ から $\mathbb{R}$ への連続な単射 $f$ が存在すると仮定して矛盾を導く。以下 $m = n - 1$ とおいて $\mathbb{R}^n = \mathbb{R} \times \mathbb{R}^m$ とみなし、また $\langle x,y \rangle \in \mathbb{R} \times \mathbb{R}^m$ に対して $f( \langle x,y \rangle )$ を $f(x,y)$ とかく。
$C$ の内点 $\langle a, b \rangle \ ( a \in \mathbb{R} \land b \in \mathbb{R}^m )$ をとり、$a$ を内点にもつ $\mathbb{R}$ の閉区間 $A$ と、$\mathbb{R}^m$ における $b$ の近傍 $B$ を、$A \times B \subseteq C$ となるようにとる($A, B$ を十分小さくとれば可能)。
$A$ から $\mathbb{R}$ への写像 $g$ を $g(x) = f(x,b)$ によって定めると、$f$ が $A \times B$ で連続な単射だから、【補題7】より $g$ も $A$ で連続な単射である。$A$ はコンパクトで $\mathbb{R}$ はハウスドルフだから、【定理6】より
\begin{equation} \tag{6}
\forall x \in A \, ( {}^*g[ \mathrm{monad}_A(x) ] = \mathrm{monad}_{g[A]}(f(x)) )
\end{equation}
が成立する。また $A$ は $\mathbb{R}$ の区間だから連結で、その連続写像 $g$ による像 $g[A]$ も連結だから $\mathbb{R}$ の区間である。$A$ は2点以上をもち $g$ は単射だから $g[A]$ も2点以上をもち、従って内点 $c$ がとれる。この $c$ に対し $\mathrm{monad}_{\mathbb{R}}(c) \subseteq {}^*(g[A])$ であり、よって
\begin{equation*}
\mathrm{monad}_{g[A]}(c) = \mathrm{monad}_{\mathbb{R}}(c) \cap {}^*(g[A]) = \mathrm{monad}_{\mathbb{R}}(c)
\end{equation*}
である。$f(a') = c$ となる $a' \in A$ をとると、$(6)$より
\begin{equation} \tag{7}
{}^*g[ \mathrm{monad}_A(a') ] = \mathrm{monad}_{g[A]}(c) = \mathrm{monad}_{\mathbb{R}}(c)
\end{equation}
が成り立つ。
この $a'$ に対し、$B$ から $\mathbb{R}$ への写像 $h$ を $h(y) = f(a',y)$ によって定める。$b$ は $\mathbb{R}^m$ の位相における $B$ の内点だから $\mathrm{monad}_{\mathbb{R}^m}(b) \subseteq {}^*B$ であり、よって
\begin{equation*}
\mathrm{monad}_B(b) = \mathrm{monad}_{\mathbb{R}^m}(b) \cap {}^*B = \mathrm{monad}_{\mathbb{R}^m}(b)
\end{equation*}
であるから、$v \neq b$ となる $v \in \mathrm{monad}_B(b)$ がとれる。【補題7】より $h$ も $B$ で連続だから、【定理2】より ${}^*h(v) \in \mathrm{monad}_{h[B]}(c) \subseteq \mathrm{monad}_{\mathbb{R}}(c)$ である。$(7)$より ${}^*g(u) = {}^*h(v)$ となる $u \in \mathrm{monad}_A(a')$ がとれ、${}^*f(u,b) = {}^*g(u)$ かつ ${}^*f(a',v) = {}^*h(v)$ より ${}^*f(u,b) = {}^*f(a',v)$ が得られるが、$f$ は単射だから ${}^*f$ も単射であり、$\langle u, b \rangle \neq \langle a', v \rangle$ だからこれは矛盾である。□
直線と平面が同じ濃度を持つことを発見したカントルがその事実に困惑したのを見て、デデキントがカントルを慰める?ために指摘した内容を、ここでは超準解析を用いて証明してみました。
(続く)(前記事)(目次)
神戸市の町外れを走る神姫バス3路線に乗る [バス]
仕事納めも終え、気分転換に年内最後の乗りバスに出かけました。
今回は神戸市の西部を走る神姫バスの路線です。
政令都市神戸には市営バスがありますが、北区や西区には一部を除いて市営バスが走らない地域が広がっています。もともとあった市営バス路線も阪急バスや神姫バスへ譲渡されました。今回、神戸市西区などを走る神姫バスの比較的長い路線を3本乗ってきました。
まずはJR大久保駅から、岩岡町を通って西神中央駅に行く路線に乗ります。岩岡町方面へは西神中央駅行が1時間に1本、途中の上岩岡行が1時間に2本あり、本数は多い方です。
JR大久保駅は明石市内なので、かつては明石市営バスのほか、今回乗った路線も昔は神戸市営バスの路線だったので、神姫バスと合わせて3社が乗り入れていましたが、今は全部神姫バスになっています。

明石市内の高丘ニュータウンを通り抜けます。元明石市営だった大久保駅から高丘までの路線もあります。

高丘を通り抜けると、すぐに神戸市西区になります。明石市の北側に覆いかぶさるように神戸市が広がっています。

岩岡町の集落に入ると片側1車線になり、ため池の多い田園地域を走っていきます。



神出町を通り抜けると広い道路に入り、グリコピアのある西神工業団地を通り抜けます。



約50分で西神中央駅に到着しました。

昼間だからか、広い広い駅前バスプールもガラガラです。

地下鉄に乗って名谷駅へ移動します。ここは須磨区なので市営バスがメインで、他に山陽バスと神姫バスが乗り入れていますが、神姫バスは今回乗る明石駅行の路線しかなく、本数も2時間に1本ほどと少なめです。

明石駅行の神姫バスに乗り、まずは須磨ニュータウン内の白川台地区に向かいます。


白川台を抜けると途端に山間部に入り、産業施設と田畑が点在する布施畑地区を通ります。


阪神高速北神戸線と山陽自動車道(淡路島への接続支線)が交差する布施畑ジャンクションを下から見ながら通ります。

小さなトンネルを抜けると、割と風格ありそうな太山寺を通り、伊川谷町の田園地域に入っていきます。



地下鉄の伊川谷駅に立ち寄り、ロードサイド店の多い伊川谷町の市街地を通っていきます。山陽新幹線からよく見える地域です。



約50分で明石駅に到着です。明石駅前は神姫バスばかりの一大ターミナルになりました。

JRで神戸駅に移動し、本日3本目の神姫バスに乗ります。今度は「快速」白川台方面の路線のうち、1日1本しか走らない押部谷(栄)行です。
途中の白川台行を含めても決して多いとは言えない本数ですが、意外とかなりの乗客があって驚きました。座席が全て埋まり立ち客も出る状況です。

新開地、湊川を経由し、山麓線から夢野白川線を登っていきます。


須磨ニュータウン内の白川峠から白川台の間で、僕以外の全ての乗客が下車していきました。神戸駅から30分弱で、運賃はなんと市内均一の210円。地下鉄とバスを乗り継ぐよりずっとコスパがいいので、これは混雑するのも納得です。

乗客が僕一人になったバスは、山陽自動車道に沿った山の中を押部谷に向かって走っていきます。



市街地からちょっと離れただけで、冬枯れの雑木林が続く不思議な光景になります。
神戸駅から約40分で、神姫ゾーンバスの本社と営業所がある押部谷(栄)に到着です。


栄駅まで少し歩いて、神戸電鉄粟生線に乗って帰ります。

神姫バスの営業エリアは基本的に明石以西ですが、意外と神戸市内にもニッチな路線があり、乗ってみるといろんな景色が味わえて面白かったです。良い2023年の乗りバス納めになりました。
「路線バス歩き」のすすめ(目次)へ
今回は神戸市の西部を走る神姫バスの路線です。
政令都市神戸には市営バスがありますが、北区や西区には一部を除いて市営バスが走らない地域が広がっています。もともとあった市営バス路線も阪急バスや神姫バスへ譲渡されました。今回、神戸市西区などを走る神姫バスの比較的長い路線を3本乗ってきました。
まずはJR大久保駅から、岩岡町を通って西神中央駅に行く路線に乗ります。岩岡町方面へは西神中央駅行が1時間に1本、途中の上岩岡行が1時間に2本あり、本数は多い方です。
JR大久保駅は明石市内なので、かつては明石市営バスのほか、今回乗った路線も昔は神戸市営バスの路線だったので、神姫バスと合わせて3社が乗り入れていましたが、今は全部神姫バスになっています。

明石市内の高丘ニュータウンを通り抜けます。元明石市営だった大久保駅から高丘までの路線もあります。

高丘を通り抜けると、すぐに神戸市西区になります。明石市の北側に覆いかぶさるように神戸市が広がっています。

岩岡町の集落に入ると片側1車線になり、ため池の多い田園地域を走っていきます。



神出町を通り抜けると広い道路に入り、グリコピアのある西神工業団地を通り抜けます。



約50分で西神中央駅に到着しました。

昼間だからか、広い広い駅前バスプールもガラガラです。

地下鉄に乗って名谷駅へ移動します。ここは須磨区なので市営バスがメインで、他に山陽バスと神姫バスが乗り入れていますが、神姫バスは今回乗る明石駅行の路線しかなく、本数も2時間に1本ほどと少なめです。


明石駅行の神姫バスに乗り、まずは須磨ニュータウン内の白川台地区に向かいます。


白川台を抜けると途端に山間部に入り、産業施設と田畑が点在する布施畑地区を通ります。


阪神高速北神戸線と山陽自動車道(淡路島への接続支線)が交差する布施畑ジャンクションを下から見ながら通ります。

小さなトンネルを抜けると、割と風格ありそうな太山寺を通り、伊川谷町の田園地域に入っていきます。



地下鉄の伊川谷駅に立ち寄り、ロードサイド店の多い伊川谷町の市街地を通っていきます。山陽新幹線からよく見える地域です。



約50分で明石駅に到着です。明石駅前は神姫バスばかりの一大ターミナルになりました。

JRで神戸駅に移動し、本日3本目の神姫バスに乗ります。今度は「快速」白川台方面の路線のうち、1日1本しか走らない押部谷(栄)行です。

途中の白川台行を含めても決して多いとは言えない本数ですが、意外とかなりの乗客があって驚きました。座席が全て埋まり立ち客も出る状況です。

新開地、湊川を経由し、山麓線から夢野白川線を登っていきます。


須磨ニュータウン内の白川峠から白川台の間で、僕以外の全ての乗客が下車していきました。神戸駅から30分弱で、運賃はなんと市内均一の210円。地下鉄とバスを乗り継ぐよりずっとコスパがいいので、これは混雑するのも納得です。

乗客が僕一人になったバスは、山陽自動車道に沿った山の中を押部谷に向かって走っていきます。



市街地からちょっと離れただけで、冬枯れの雑木林が続く不思議な光景になります。
神戸駅から約40分で、神姫ゾーンバスの本社と営業所がある押部谷(栄)に到着です。


栄駅まで少し歩いて、神戸電鉄粟生線に乗って帰ります。

神姫バスの営業エリアは基本的に明石以西ですが、意外と神戸市内にもニッチな路線があり、乗ってみるといろんな景色が味わえて面白かったです。良い2023年の乗りバス納めになりました。
「路線バス歩き」のすすめ(目次)へ
さよなら金剛バス 葛城山を下り水越峠からの金剛バスに名残の乗車 [バス]
南河内を運行エリアとする金剛バスにはこれまでも何回か乗車しましたが、このたびついに運営会社の金剛自動車から、2023年12月21日をもって路線バス事業を廃止することが発表されました。
それ以降の地域の公共交通をどうするかは関係市町村による協議会で議論されてきており、このほどその内容も決定されました。次のサイトから内容を知ることができます。
令和5年度第4回富田林市、太子町、河南町及び千早赤阪村地域公共交通活性化協議会資料・議事概要
これによると、現在の金剛バス15路線のうち主要5路線は近鉄バスと南海バスへ引き継がれ、その他の多くは自治体の「自治体有償旅客運送」に引き継がれます。完全に廃止される区間もいくつかあり、その中の一つに千早線の東水分〜水越峠間(休日のみ運行)があったので、廃止される前に名残乗車をしてきました。
今回のルートはこちら。ロープウェイで葛城山に登り、水越峠まで山道を下って、そこから金剛バスで富田林駅まで乗るという、ハイキングと乗りバスを組み合わせた行程です。
まず葛城山に登るために、近鉄御所駅からロープウェイの葛城登山口駅まで奈良交通バスに乗ります。しかしロープウェイはほぼ30分に1本運行しているのに、そこへのアクセスバスが臨時を入れても1時間に1本しかないのは不便です。

色づいた山肌を見ながら、バスは山麓を登って行きます。


バスの終点でロープウェイに乗り換えます。このロープウェイは近鉄直営ですが、昨今の情勢からこれもいつ廃止されるかわかりません(南隣の金剛山にアクセスする千早赤阪村営ロープウェイは、2019年より休止となり、そのまま廃止が決定してしまいました)。



ロープウェイからは奈良盆地を見下ろす素晴らしい景色です。


ロープウェイを降りて紅葉の散策路を少し歩くと、葛城山上に着きます。



この季節はススキの原が綺麗で、天気がよかったので大阪湾までよく見えました。


山頂付近の白樺食堂でうどんを食べて休憩したら、水越峠に向けて約2km強の山下りです。「ダイヤモンドトレール」という名前がつけられた金剛葛城山系を縦走する登山道で、金剛山や岩湧山にも通じています。




この道は階段が延々と続くのですが、1段あたりの蹴上げがかなり高いので、とても普通にトントンとは降りられません。一歩一歩膝を曲げながら慎重に降りて行かなければならず、すぐに足裏や膝が痛くなってきます。


階段をひたすら降りていき、ちょっとした岩場を越え、小川沿いの道をしばらく歩くと、水越峠の道路に出ます。




かつての国道309号線を峠から大阪府側へ少し歩くと、金剛バスの水越峠バス停に到着です。山歩きなので余裕を持った行程としたために、50分ほど早く着いてしまいました。足が疲れたのでどこかに座りたいところですが、ベンチがないので柵の基礎コンクリートに座って休憩しました。



時刻通りやって来たバスは、回転場にバックで入って向きを変え、待っていた登山客が数名乗り込みました。


バスは旧道を下り、すぐに国道に合流してさらに下って行きます。


東水分からは現在の白木線が河南町のコミュニティバスとして今後も残りますが、そちらは千早赤阪村の中心地の森屋を通らないので、実質的には森屋〜水越峠が完全廃止となります。



バイパス開通後に国道309号線から格下げになった府道705号線を通り、河南町から富田林市内へと進みます。この道での大型車どうしのすれ違いも12月20日まででおそらく見納めです。



富田林駅南口に到着しました。

たくさんの路線を走る薄緑色のバスが集まるこの光景も、もうすぐ見られなくなります。
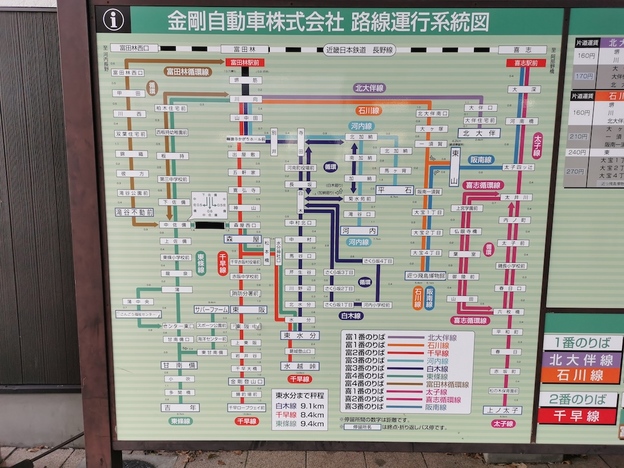
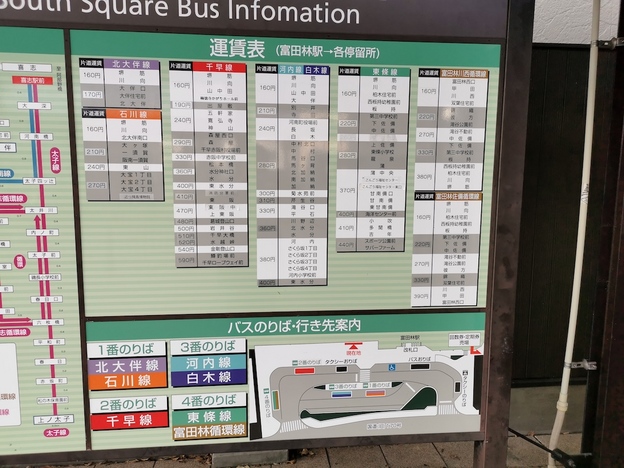

駅前の金剛自動車の本社建屋も、今後解体されていくのでしょうか。


長い間地域に密着した一つのバス会社が、時代の流れで消えていきます。公共交通の在り方に間違いなく一石を投じた事象になりそうです。
ともあれ、お疲れ様でした。最後の日まで安全運行をお願いします。
「路線バス歩き」のすすめ(目次)へ
それ以降の地域の公共交通をどうするかは関係市町村による協議会で議論されてきており、このほどその内容も決定されました。次のサイトから内容を知ることができます。
令和5年度第4回富田林市、太子町、河南町及び千早赤阪村地域公共交通活性化協議会資料・議事概要
これによると、現在の金剛バス15路線のうち主要5路線は近鉄バスと南海バスへ引き継がれ、その他の多くは自治体の「自治体有償旅客運送」に引き継がれます。完全に廃止される区間もいくつかあり、その中の一つに千早線の東水分〜水越峠間(休日のみ運行)があったので、廃止される前に名残乗車をしてきました。
今回のルートはこちら。ロープウェイで葛城山に登り、水越峠まで山道を下って、そこから金剛バスで富田林駅まで乗るという、ハイキングと乗りバスを組み合わせた行程です。
まず葛城山に登るために、近鉄御所駅からロープウェイの葛城登山口駅まで奈良交通バスに乗ります。しかしロープウェイはほぼ30分に1本運行しているのに、そこへのアクセスバスが臨時を入れても1時間に1本しかないのは不便です。


色づいた山肌を見ながら、バスは山麓を登って行きます。


バスの終点でロープウェイに乗り換えます。このロープウェイは近鉄直営ですが、昨今の情勢からこれもいつ廃止されるかわかりません(南隣の金剛山にアクセスする千早赤阪村営ロープウェイは、2019年より休止となり、そのまま廃止が決定してしまいました)。



ロープウェイからは奈良盆地を見下ろす素晴らしい景色です。


ロープウェイを降りて紅葉の散策路を少し歩くと、葛城山上に着きます。



この季節はススキの原が綺麗で、天気がよかったので大阪湾までよく見えました。


山頂付近の白樺食堂でうどんを食べて休憩したら、水越峠に向けて約2km強の山下りです。「ダイヤモンドトレール」という名前がつけられた金剛葛城山系を縦走する登山道で、金剛山や岩湧山にも通じています。




この道は階段が延々と続くのですが、1段あたりの蹴上げがかなり高いので、とても普通にトントンとは降りられません。一歩一歩膝を曲げながら慎重に降りて行かなければならず、すぐに足裏や膝が痛くなってきます。


階段をひたすら降りていき、ちょっとした岩場を越え、小川沿いの道をしばらく歩くと、水越峠の道路に出ます。




かつての国道309号線を峠から大阪府側へ少し歩くと、金剛バスの水越峠バス停に到着です。山歩きなので余裕を持った行程としたために、50分ほど早く着いてしまいました。足が疲れたのでどこかに座りたいところですが、ベンチがないので柵の基礎コンクリートに座って休憩しました。



時刻通りやって来たバスは、回転場にバックで入って向きを変え、待っていた登山客が数名乗り込みました。


バスは旧道を下り、すぐに国道に合流してさらに下って行きます。


東水分からは現在の白木線が河南町のコミュニティバスとして今後も残りますが、そちらは千早赤阪村の中心地の森屋を通らないので、実質的には森屋〜水越峠が完全廃止となります。



バイパス開通後に国道309号線から格下げになった府道705号線を通り、河南町から富田林市内へと進みます。この道での大型車どうしのすれ違いも12月20日まででおそらく見納めです。



富田林駅南口に到着しました。

たくさんの路線を走る薄緑色のバスが集まるこの光景も、もうすぐ見られなくなります。



駅前の金剛自動車の本社建屋も、今後解体されていくのでしょうか。


長い間地域に密着した一つのバス会社が、時代の流れで消えていきます。公共交通の在り方に間違いなく一石を投じた事象になりそうです。
ともあれ、お疲れ様でした。最後の日まで安全運行をお願いします。
「路線バス歩き」のすすめ(目次)へ
志賀高原から軽井沢へ 観光ゴールデンルートを路線バスで行く [バス]
子供の頃、修学旅行で軽井沢から鬼押出しを通って志賀高原に貸切バスで行ったことがあります。当時は一般路線バスもたくさん走っていた観光ゴールデンルートだったでしょう。現在でもこのルートを路線バスで通り抜けることは可能ですが、志賀高原と草津温泉をつなぐ路線が1日1本しかなく、いつ廃止になってしまうかわからないので、今のうちに乗ってくることにしました。
今回のルートはこちら。修学旅行とは逆方向に志賀高原から軽井沢に向かうルートで、間にJR吾妻線を挟むことにしました。
(最初の一部ログを取り忘れてワープしています。)
草津温泉から万座・鹿沢口を結ぶバスを使えば全部バスで繋がりますが、志賀高原からのバスとの乗継がうまくいかないので今回は諦めました。また、草津温泉から直接軽井沢を結ぶ草軽交通のバスも惹かれたのですが、今回は鬼押出しをもう一度見たかったので、JRを挟んだこのルートにしました。
大阪からJR夜行高速バスで長野に向かいます。4列シートは安いですがやはりちょっとしんどい。

早朝6時台に長野駅前に到着。カフェも何も開いてないので、コンビニでサンドイッチを買って地下の長野電鉄のりばのベンチで腹ごしらえです。



実は長野電鉄を乗り通すのも今回が初めてなので楽しみでした。残念ながら特急の走る時間帯ではないので、信州中野乗り継ぎの全線各停になりました。

リンゴ畑の中を走る電車を堪能して、湯田中駅に到着です。



湯田中駅は志賀高原方面に向かう長電バスの拠点で、駅前にはたくさんのバスが並んでいます。



今回乗る草津温泉行きのバスは長野駅から出発し、湯田中駅を通らないので、一般路線で「スノーモンキーパーク」へ行って乗り換えと案内されています。しかし草津温泉行が途中停車する「道の駅やまのうち」が湯田中駅から歩いて20分ほどなので、そこから直接乗ることにしました。

鄙びた温泉街と、リンゴ畑を通り抜けると、すぐに「道の駅やまのうち」の停留所です。駐車場の中にポツンと標柱があります。



長野駅から来る急行バスなので、観光バス仕様です。


志賀高原に登っていき、途中の「志賀高原山の家」でトイレ休憩を取ります。



スキー場のリフトを横目で見ながら、県境の渋峠を目指します。




峠を越えるといきなり霧の中になりました。白根火山も残念ながら見えません。



山道を下って、草津温泉に到着です。


夜行バスの疲れをようやく温泉で癒すことができました。


昼食を取って、長野原草津口行のJRバスに乗ります。これも急行バスで、終点まで直行です。




JR吾妻線で万座・鹿沢口まで移動します。この一駅先の大前が吾妻線の終点ですが、そこまで行く電車の本数は少なく、今回乗った電車も万座・鹿沢口止まりでした。


この駅もバスの乗換拠点ですが、駅構内のバス時刻表が全然メンテされておらず機能停止しています。


軽井沢駅行の西武観光バスに乗り、鬼押ハイウェーに向かいます。


高原の木々の中を真っ直ぐ走り、鬼押出し園で途中下車します。



溶岩がゴロゴロ転がっている光景は見応えありましたが、曇っていて浅間山が見えないのは残念でした。



1時間後のバスに乗って、軽井沢駅に向かいます。



洒落た店が並ぶ街並みを通り抜けて、軽井沢駅に到着しました。


かつての碓氷峠の拠点駅だった軽井沢駅は、新幹線駅としなの鉄道の終着駅になりました。しなの鉄道の駅は旧駅舎が再現されています。




軽井沢観光などという上流階級の遊びはせずに、また夜行バスで帰ります。今度は千曲バスの3列シートで楽々でした(夜中にトイレに気兼ねなく行けるのが良いのです)。


天気がいまひとつだったのが残念ですが、修学旅行の思い出のルートを路線バスで辿り、昭和感あふれる観光地を再訪して感傷にふけることができ、有意義な秋の休日でした。
「路線バス歩き」のすすめ(目次)へ
今回のルートはこちら。修学旅行とは逆方向に志賀高原から軽井沢に向かうルートで、間にJR吾妻線を挟むことにしました。
(最初の一部ログを取り忘れてワープしています。)
草津温泉から万座・鹿沢口を結ぶバスを使えば全部バスで繋がりますが、志賀高原からのバスとの乗継がうまくいかないので今回は諦めました。また、草津温泉から直接軽井沢を結ぶ草軽交通のバスも惹かれたのですが、今回は鬼押出しをもう一度見たかったので、JRを挟んだこのルートにしました。
大阪からJR夜行高速バスで長野に向かいます。4列シートは安いですがやはりちょっとしんどい。

早朝6時台に長野駅前に到着。カフェも何も開いてないので、コンビニでサンドイッチを買って地下の長野電鉄のりばのベンチで腹ごしらえです。



実は長野電鉄を乗り通すのも今回が初めてなので楽しみでした。残念ながら特急の走る時間帯ではないので、信州中野乗り継ぎの全線各停になりました。

リンゴ畑の中を走る電車を堪能して、湯田中駅に到着です。



湯田中駅は志賀高原方面に向かう長電バスの拠点で、駅前にはたくさんのバスが並んでいます。



今回乗る草津温泉行きのバスは長野駅から出発し、湯田中駅を通らないので、一般路線で「スノーモンキーパーク」へ行って乗り換えと案内されています。しかし草津温泉行が途中停車する「道の駅やまのうち」が湯田中駅から歩いて20分ほどなので、そこから直接乗ることにしました。

鄙びた温泉街と、リンゴ畑を通り抜けると、すぐに「道の駅やまのうち」の停留所です。駐車場の中にポツンと標柱があります。



長野駅から来る急行バスなので、観光バス仕様です。


志賀高原に登っていき、途中の「志賀高原山の家」でトイレ休憩を取ります。



スキー場のリフトを横目で見ながら、県境の渋峠を目指します。




峠を越えるといきなり霧の中になりました。白根火山も残念ながら見えません。



山道を下って、草津温泉に到着です。


夜行バスの疲れをようやく温泉で癒すことができました。


昼食を取って、長野原草津口行のJRバスに乗ります。これも急行バスで、終点まで直行です。




JR吾妻線で万座・鹿沢口まで移動します。この一駅先の大前が吾妻線の終点ですが、そこまで行く電車の本数は少なく、今回乗った電車も万座・鹿沢口止まりでした。


この駅もバスの乗換拠点ですが、駅構内のバス時刻表が全然メンテされておらず機能停止しています。


軽井沢駅行の西武観光バスに乗り、鬼押ハイウェーに向かいます。


高原の木々の中を真っ直ぐ走り、鬼押出し園で途中下車します。



溶岩がゴロゴロ転がっている光景は見応えありましたが、曇っていて浅間山が見えないのは残念でした。



1時間後のバスに乗って、軽井沢駅に向かいます。



洒落た店が並ぶ街並みを通り抜けて、軽井沢駅に到着しました。


かつての碓氷峠の拠点駅だった軽井沢駅は、新幹線駅としなの鉄道の終着駅になりました。しなの鉄道の駅は旧駅舎が再現されています。




軽井沢観光などという上流階級の遊びはせずに、また夜行バスで帰ります。今度は千曲バスの3列シートで楽々でした(夜中にトイレに気兼ねなく行けるのが良いのです)。


天気がいまひとつだったのが残念ですが、修学旅行の思い出のルートを路線バスで辿り、昭和感あふれる観光地を再訪して感傷にふけることができ、有意義な秋の休日でした。
「路線バス歩き」のすすめ(目次)へ
ハノイメトロに乗ってきた [鉄道]
3年ぶりの海外旅行で、ベトナムのハノイに行ってきました。
大きな目的の一つは、やはりベトナム初(で現時点唯一)の都市鉄道であるハノイメトロに乗ってくることです。
ハノイメトロ公式ページ
公式ページに掲載されている Google Map 路線図
ベトナムの都市鉄道は、計画路線だけは何年も前からたくさんあるのですが、どういうわけか工事がなかなか進まず、ハノイで現時点開業できているのは2A号線の Cát Linh と Yên Nghĩa の間だけです。
ハノイ駅から西に伸びる3号線が開業すれば観光客にも便利になるのでしょうけれど、工事中でまだまだ先になりそうです。
南の最大都市ホーチミンには未だに1路線も開業していません。
余談ですが、今回はツアー料金を若干奮発して、ロッテホテルに宿泊しました。ハノイで最も高い65階建てビルの上層階がホテルになっており、部屋からの眺めが最高なのでお勧めです。

ちなみにこの写真の右下の池に沿って見えるのが、工事中の3号線です。この場所で高架から地下に潜ります。
ロッテホテルから少し歩いて工事中の現場の脇を通り、バスに乗って Cát Linh 駅に向かいます。ハノイのバスは Google Map で路線が検索できるので、意外と使いやすいです。

Cát Linh 駅は綺麗なビルになっています。

こんな券売機で切符を買います。英語表示があるので迷わないです。

電車は緑色をシンボルカラーとしています。昼間だったからか空いていました。


高架鉄道は街並みが上から見えるので楽しいです。(↓動画)
終点の Yên Nghĩa まで乗りました。



改札機はICカード式で、入場時にタッチ、出場時は回収される方式です。

Yên Nghĩa 駅のすぐそばに郊外へ向かうバスターミナルがあるので、ちょっと立ち寄ってみました。

昼間だったからか、乗客らしき人がほとんどおらず、切符売り場も閑散としています。


バスもたくさん停まってはいるのですが発着する様子がありません。バスの行き先で僕が知っている地名は Hải Phòng くらいだったので、地元向けのちょっとマイナーすぎるバスターミナルだったのかもしれません。




他に見るところもないので、メトロに乗って戻ります。

途中の Láng 駅で下車し、近くの Vincom Mega Mall Royal City で買い物と昼食を取りました。この路線の沿線で旅行者が楽しめるところはここくらいかもしれません。



久しぶりに訪れたハノイは、夜も店が多くて明るく楽しい町でした。メトロ3号線をはじめ、早く都市鉄道網が充実してもっと便利になってほしいです。

大きな目的の一つは、やはりベトナム初(で現時点唯一)の都市鉄道であるハノイメトロに乗ってくることです。
ハノイメトロ公式ページ
公式ページに掲載されている Google Map 路線図
ベトナムの都市鉄道は、計画路線だけは何年も前からたくさんあるのですが、どういうわけか工事がなかなか進まず、ハノイで現時点開業できているのは2A号線の Cát Linh と Yên Nghĩa の間だけです。
ハノイ駅から西に伸びる3号線が開業すれば観光客にも便利になるのでしょうけれど、工事中でまだまだ先になりそうです。
南の最大都市ホーチミンには未だに1路線も開業していません。
余談ですが、今回はツアー料金を若干奮発して、ロッテホテルに宿泊しました。ハノイで最も高い65階建てビルの上層階がホテルになっており、部屋からの眺めが最高なのでお勧めです。

ちなみにこの写真の右下の池に沿って見えるのが、工事中の3号線です。この場所で高架から地下に潜ります。
ロッテホテルから少し歩いて工事中の現場の脇を通り、バスに乗って Cát Linh 駅に向かいます。ハノイのバスは Google Map で路線が検索できるので、意外と使いやすいです。

Cát Linh 駅は綺麗なビルになっています。

こんな券売機で切符を買います。英語表示があるので迷わないです。

電車は緑色をシンボルカラーとしています。昼間だったからか空いていました。


高架鉄道は街並みが上から見えるので楽しいです。(↓動画)
終点の Yên Nghĩa まで乗りました。



改札機はICカード式で、入場時にタッチ、出場時は回収される方式です。

Yên Nghĩa 駅のすぐそばに郊外へ向かうバスターミナルがあるので、ちょっと立ち寄ってみました。

昼間だったからか、乗客らしき人がほとんどおらず、切符売り場も閑散としています。


バスもたくさん停まってはいるのですが発着する様子がありません。バスの行き先で僕が知っている地名は Hải Phòng くらいだったので、地元向けのちょっとマイナーすぎるバスターミナルだったのかもしれません。




他に見るところもないので、メトロに乗って戻ります。

途中の Láng 駅で下車し、近くの Vincom Mega Mall Royal City で買い物と昼食を取りました。この路線の沿線で旅行者が楽しめるところはここくらいかもしれません。



久しぶりに訪れたハノイは、夜も店が多くて明るく楽しい町でした。メトロ3号線をはじめ、早く都市鉄道網が充実してもっと便利になってほしいです。

わかってない奴がわかったつもりで書き留める超準解析(その18) [数学]
【超準解析について生半可な知識しかない僕が、わかったつもりの内容をちょっとずつ書き留めていきます。不正確な内容や誤りもあることをご承知ください。】
(18) アレクサンドロフの1点コンパクト化
前回の続きとして、コンパクトでない空間をコンパクト空間に拡張する1つの手法「アレクサンドロフの1点コンパクト化」を、超準モデルを使って構成する方法を紹介します。
1. 超準モデルから定まる位相
$X$ を位相が定まっていない無限集合とするとき、その超準モデルを使って、次のようにして $X$ に位相を定めることができます。
すべての $X$ の点 $x$ に対して $x \in \nu(x)$ をみたす ${}^*X$ の部分集合 $\nu(x) \in \mathscr{P}({}^*X)$ が(何でもよいので)定まっているとします。このとき、
\begin{equation*}
\mathcal{O} = \{ \, A \in \mathscr{P}(X) \, \mid \, \forall x \in A \, (\nu(x) \subseteq {}^*A) \, \}
\end{equation*}
と定めると、この $\mathcal{O}$ は次の開集合系の性質を全てみたします。
① $\emptyset \in \mathcal{O} \land X \in \mathcal{O}$
② $A \in \mathcal{O} \land B \in \mathcal{O} \to A \cap B \in \mathcal{O}$
③ $\forall i \in I \, (A_i \in \mathcal{O}) \to \bigcup_{i \in I} A_i \in \mathcal{O}$
①と②は明らかなので、和集合に関する性質③だけ示しておきます。$\forall i \in I \, (A_i \in \mathcal{O})$ が成り立つとし、$B = \bigcup_{i \in I} A_i$ とします。任意に $x \in B$ をとると、ある $i \in I$ に対して $x \in A_i$ だから $\nu(x) \subseteq {}^*A_i$ となります。$A_i \subseteq B$ だから移行原理より ${}^*A_i \subseteq {}^*B$ となり、従って $\nu(x) \subseteq {}^*B$ となるから $B \in \mathcal{O}$ です。これで $\mathcal{O}$ が開集合系の性質を全てみたすことが示されたので、$X$ に位相が定まります。
この位相に関して近傍系やモナドが定まりますが、$A$ が点 $x$ の近傍ならば簡単な考察により $\nu(x) \subseteq {}^*A$ がわかるので、$\nu(x) \subseteq \mathrm{monad}(x)$ となります。一般には必ずしもこれらは等しくなりません。
この方法を使って位相空間 $X$ を $X \subsetneq Y$ となる集合 $Y$ に拡張することを考えます。このため、一般に一方が他方の部分位相空間となるための超準モデルによる同値条件を考察します。
$X \subseteq Y$ の関係にある位相空間 $X, Y$ がそれぞれあるとします。$X$ と $Y$ の開集合系をそれぞれ $\mathcal{O}_X, \mathcal{O}_Y$ とし、また、$X$ における点 $x$ の近傍系とモナドをそれぞれ $\mathcal{N}_X(x), \mathrm{monad}_X(x)$ とかき、同様に $Y$ における点 $x$ の近傍系とモナドをそれぞれ $\mathcal{N}_Y(x), \mathrm{monad}_Y(x)$ とかくことにします。このとき、$X$ が $Y$ の部分位相空間であるとは、
\begin{equation} \tag{1}
\forall A \in \mathscr{P}(X) \, (A \in \mathcal{O}_X \leftrightarrow \exists B \in \mathcal{O}_Y \, (A = B \cap X))
\end{equation}
であることをいいます。
これを超準モデルでの同値条件で表したものが次の定理です。
(証明)$(1) \Leftrightarrow (2)$ を示せばよい。
$(1) \Rightarrow (2)$ : $(1)$ が成り立つとし、任意に $x \in X$ をとる。
任意に $B \in \mathcal{N}_Y(x)$ をとると、$x \in B' \subseteq B$ となる $B' \in \mathcal{O}_Y$ がとれ、$A' = B' \cap X$ とすると $(1)$ より $A' \in \mathcal{O}_X$ で、$x \in A'$ だから
\begin{equation*}
\mathrm{monad}_X(x) \subseteq {}^*A' \subseteq {}^*B' \subseteq {}^*B
\end{equation*}
である。$B \in \mathcal{N}_Y(x)$ は任意だから $\mathrm{monad}_X(x) \subseteq \mathrm{monad}_Y(x)$ であり、また $\mathrm{monad}_X(x) \subseteq {}^*X$ は明らかだから $\mathrm{monad}_X(x) \subseteq \mathrm{monad}_Y(x) \cap {}^*X$ が得られる。
逆に、任意に $A \in \mathcal{N}_X(x)$ をとると、$x \in A' \subseteq A$ となる $A' \in \mathcal{O}_X$ がとれ、$(1)$ よりある $B' \in \mathcal{O}_Y$ に対して $A' = B' \cap X$ となり、$x \in B'$ だから $\mathrm{monad}_Y(x) \subseteq {}^*B'$ より
\begin{equation*}
\mathrm{monad}_Y(x) \cap {}^*X \subseteq {}^*B' \cap {}^*X = {}^*A' \subseteq {}^*A
\end{equation*}
であり、$A \in \mathcal{N}_X(x)$ は任意だから $\mathrm{monad}_Y(x) \cap {}^*X \subseteq \mathrm{monad}_X(x)$ が得られる。
以上より $\mathrm{monad}_X(x) = \mathrm{monad}_Y(x) \cap {}^*X$ であり、$(2)$ が示された。
$(2) \Rightarrow (1)$ : $(2)$ が成り立つとし、任意に $A \in \mathscr{P}(X)$ をとる。
$A \in \mathcal{O}_X$ とする。$B' = A \cup (Y \setminus X)$ とおき、任意の $x \in A$ に対して $\mathrm{monad}_Y(x) \subseteq {}^*B'$ となることを示す。任意に $y \in \mathrm{monad}_Y(x)$ をとると、$y \in {}^*X$ ならば $(2)$ より
\begin{equation*}
y \in \mathrm{monad}_Y(x) \cap {}^*X = \mathrm{monad}_X(x) \subseteq {}^*A \subseteq {}^*B'
\end{equation*}
となるから $y \in {}^*B'$ である。$y \notin {}^*X$ ならば
\begin{equation*}
y \in {}^*Y \setminus {}^*X = {}^*(Y \setminus X) \subseteq {}^*B'
\end{equation*}
よりやはり $y \in {}^*B'$ である。これで $\mathrm{monad}_Y(x) \subseteq {}^*B'$ が示されたから $B' \in \mathcal{N}_Y(x)$ であり、$x \in B(x) \subseteq B'$ をみたす $B(x) \in \mathcal{O}_Y$ が存在する。$B = \bigcup_{x \in A}B(x)$ とおくと $B \in \mathcal{O}_Y$ かつ $B \subseteq B'$ で、明らかに $A \subseteq B \cap X$ であり、また $B \cap X \subseteq B' \cap X = A$ だから $A = B \cap X$ である。
逆に、ある $B \in \mathcal{O}_Y$ に対して $A = B \cap X$ ならば、任意の $x \in A$ に対して、$\mathrm{monad}_Y(x) \subseteq {}^*B$ と $(2)$ より
\begin{equation*}
\mathrm{monad}_X(x) = \mathrm{monad}_Y(x) \cap {}^*X \subseteq {}^*B \cap {}^*X = {}^*A
\end{equation*}
が得られるから、$A \in \mathcal{O}_X$ である。
以上より $A \in \mathcal{O}_X \leftrightarrow \exists B \in \mathcal{O}_Y \, (A = B \cap X)$ であり、$(1)$ が示された。□
さて、超準モデルを使って位相空間 $X$ を $X \subsetneq Y$ となる $Y$ に拡張する一つの方法を、次の補題によって示します。
(証明)
任意に $x \in X$ をとる。まず、$\mathrm{monad}_X(x) = \nu(x) \subseteq \mathrm{monad}_Y(x)$ である。逆の包含関係を示すため、任意に $A \in \mathcal{N}_X(x)$ をとると、$x \in B \subseteq A$ となる $B \in \mathcal{O}_X$ が存在し、$\forall y \in B \, (\nu(y) = \mathrm{monad}_X(y) \subseteq {}^*B)$ より $B \in \mathcal{O}_Y$ となるから $A \in \mathcal{N}_Y(x)$ であり、これより $\mathrm{monad}_Y(x) \subseteq {}^*A$ である。$A \in \mathcal{N}_X(x)$ は任意だから $\mathrm{monad}_Y(x) \subseteq \mathrm{monad}_X(x)$ が得られる。以上で $(3)$ が示された。□
この補題の方法は、本来は $(2)$ でよいのにそれより強い $(3)$ が得られることから、位相空間の拡張手段としてはかなり「雑」といえます。しかし次に示す目的のためには、この方法で十分です。
2. アレクサンドロフの1点コンパクト化
ここまでの考察を利用して、「アレクサンドロフの1点コンパクト化」を超準モデルを用いて構成します。
位相空間 $X$ に対し、$X$ に属さない1点 $\infty$ を $X$ に追加した空間 $Y = X \cup \{ \infty \}$ を考え、次によって $\nu(\infty)$ を定めます。
\begin{equation*}
\nu(\infty) = \{ \, y \in {}^*X \, \mid \, \forall x \in X \, (y \notin \mathrm{monad}_X(x)) \, \} \cup \{ \infty \}
\end{equation*}
つまり「 ${}^*X$ のすべての遠標準点と $\infty$ を集めた集合」を $\nu(\infty)$ と定めます。
これを用いて【補題2】の方法で $X$ を部分位相空間とする $Y$ の位相が定まります。$(3)$ が成立するので、以下 $\mathrm{monad}$ の添字は省略します。
このとき、まず $Y$ はコンパクトです。なぜなら任意に $y \in {}^*Y$ をとると、$y$ はある $x \in X$ に対して $y \in \mathrm{monad}(x)$ となるか、または $y \in \nu(\infty)$ となるかのどちらかで、後者ならば $y \in \nu(\infty) \subseteq \mathrm{monad}(\infty)$ なので、第17回【定理5】より $Y$ はコンパクトになります。
次に、$X$ がコンパクトでない場合、$X$ は $Y$ において稠密となります。なぜなら $X$ がコンパクトでなければ ${}^*X$ は遠標準点をもつから $\nu(\infty) \cap {}^*X \neq \emptyset$ であり、従って $\mathrm{monad}(\infty) \cap {}^*X \neq \emptyset$ より $\forall x \in Y \, ( \mathrm{monad}(x) \cap {}^*X \neq \emptyset )$ となるから、第17回【定理3】の ix) より $X$ は $Y$ において稠密です。
これらの条件をみたす $Y = X \cup \{ \infty \}$ を $X$ のアレクサンドロフの1点コンパクト化といいます。従って上の方法は、任意のコンパクトでない位相空間から1点コンパクト化を構成する(超準モデルを使った)一つの方法を示しています。
さらに次が成り立ちます。
(証明)
$\mathrm{monad}(\infty) \supseteq \nu(\infty)$ は既に証明済み。$\mathrm{monad}(\infty) \subseteq \nu(\infty)$ を示すため、ある $ y \in \mathrm{monad}(\infty) \setminus \nu(\infty)$ が存在すると仮定して矛盾を導く。$y \notin \nu(\infty)$ なので、$\nu(\infty)$ の定義より、ある $x \in X$ に対して $y \in \mathrm{monad}(x)$ である。$X$ は局所コンパクトだから $A \in \mathcal{N}_X(x)$ となるコンパクトな $A$ が存在して $y \in \mathrm{monad}(x) \subseteq {}^*A$ より $y \in {}^*A$ となる。$X$ はハウスドルフだから第17回【定理6】 ii) より $A$ は $X$ の閉集合で、従って $X \setminus A$ は $X$ の開集合である。そこで $B = (X \setminus A) \cup \{ \infty \}$ とすると $B = Y \setminus A$ で、任意の $z \in X \setminus A$ に対して $\nu(z) = \mathrm{monad}(z) \subseteq {}^*(X \setminus A) \subseteq {}^*B$ である。また $A$ がコンパクトだから第17回【定理5】より ${}^*A$ の点は全て ${}^*X$ の近標準点で、$\nu(\infty)$ は ${}^*X$ の遠標準点と $\infty$ の集合だから $\nu(\infty) \cap {}^*A = \emptyset$ であり、これより $\nu(\infty) \subseteq {}^*Y \setminus {}^*A = {}^*(Y \setminus A) = {}^*B$ となる。従って $B$ は $Y$ における開集合であるから $\infty$ の近傍であり、 $y \in \mathrm{monad}(\infty) \subseteq {}^*B = {}^*Y \setminus {}^*A$ となるから $y \in {}^*A$ と矛盾する。以上より $\mathrm{monad}(\infty) \subseteq \nu(\infty)$ が得られたから $\mathrm{monad}(\infty) = \nu(\infty)$ である。□
この補題を使って、次の有名な結果が示されます。
(証明)
$X$ がハウスドルフであることと第17回【定理4】 ii) より、任意の $x, y \in X$ に対して $x \neq y \to \mathrm{monad}(x) \cap \mathrm{monad}(y) = \emptyset$ である。さらに【補題3】より $\mathrm{monad}(x) \cap \mathrm{monad}(\infty) = \mathrm{monad}(x) \cap \nu(\infty) = \emptyset$ も明らかなので、任意の $x, y \in Y$ に対して $x \neq y \to \mathrm{monad}(x) \cap \mathrm{monad}(y) = \emptyset$ が成り立ち、従って再び第17回【定理4】 ii) より $Y$ もハウスドルフである。□
ついでに、この定理の逆も超準モデルを利用して示しておきましょう。そのために必要になるのが次の補題です。
(証明)
【定理1】より任意の $x \in X$ に対して
\begin{equation*}
\mathrm{monad}_X(x) = \mathrm{monad}_Y(x) \cap {}^*X
\end{equation*}
が成立する。$Y$ が $\mathrm{T}_1$ だから第17回【定理4】 i) より $\infty \notin \mathrm{monad}_Y(x)$ であり、かつ ${}^*Y = {}^*X \cup \{ \infty \}$ だから $\mathrm{monad}_Y(x) \subseteq {}^*X$ すなわち $\mathrm{monad}_Y(x) \cap {}^*X = \mathrm{monad}_Y(x)$ である。従って $(4)$ が成立する。□
この補題を使って、【定理4】の逆が次のように示されます。
(証明)
$Y$ はハウスドルフだから $\mathrm{T}_1$ であり、【補題5】より $(4)$ が成立する。従って $Y$ のハウスドルフ性と第17回【定理4】 ii) より $X$ もハウスドルフである。任意に $x \in X$ をとると、$Y$ がハウスドルフだから $Y$ における $x$ の開近傍 $A$ と $\infty$ の開近傍 $B$ で $A \cap B = \emptyset$ となるものがとれる。$C = Y \setminus B$ とすると、$C$ はコンパクト空間 $Y$ の閉集合だから、第17回【定理6】 i) より $Y$ においてコンパクトである。従って第17回【定理5】より、
\begin{equation*}
\forall y \in {}^*C \, \exists z \in C \, (y \in \mathrm{monad}_Y(z))
\end{equation*}
が成立するが、$\infty \notin C$ より $C \subseteq X$ であり、これと $(4)$ より
\begin{equation*}
\forall y \in {}^*C \, \exists z \in C \, (y \in \mathrm{monad}_X(z))
\end{equation*}
が成立し、第17回【定理5】より $C$ は $X$ においてもコンパクトである。$A \subseteq C$ だから $C$ は $x$ のコンパクトな近傍であり、$x \in X$ は任意だから $X$ は局所コンパクトである。□
以上でアレクサンドロフの1点コンパクト化に関する諸定理が、超準モデルを使って証明されました。通常の方法に比べて特に簡単になるとは言えませんが、ハウスドルフ性やコンパクト性とモナドとの関係を見通しよく利用することができて、面白い方法だと思います。
(続く)(前記事)(目次)
(18) アレクサンドロフの1点コンパクト化
前回の続きとして、コンパクトでない空間をコンパクト空間に拡張する1つの手法「アレクサンドロフの1点コンパクト化」を、超準モデルを使って構成する方法を紹介します。
1. 超準モデルから定まる位相
$X$ を位相が定まっていない無限集合とするとき、その超準モデルを使って、次のようにして $X$ に位相を定めることができます。
すべての $X$ の点 $x$ に対して $x \in \nu(x)$ をみたす ${}^*X$ の部分集合 $\nu(x) \in \mathscr{P}({}^*X)$ が(何でもよいので)定まっているとします。このとき、
\begin{equation*}
\mathcal{O} = \{ \, A \in \mathscr{P}(X) \, \mid \, \forall x \in A \, (\nu(x) \subseteq {}^*A) \, \}
\end{equation*}
と定めると、この $\mathcal{O}$ は次の開集合系の性質を全てみたします。
① $\emptyset \in \mathcal{O} \land X \in \mathcal{O}$
② $A \in \mathcal{O} \land B \in \mathcal{O} \to A \cap B \in \mathcal{O}$
③ $\forall i \in I \, (A_i \in \mathcal{O}) \to \bigcup_{i \in I} A_i \in \mathcal{O}$
①と②は明らかなので、和集合に関する性質③だけ示しておきます。$\forall i \in I \, (A_i \in \mathcal{O})$ が成り立つとし、$B = \bigcup_{i \in I} A_i$ とします。任意に $x \in B$ をとると、ある $i \in I$ に対して $x \in A_i$ だから $\nu(x) \subseteq {}^*A_i$ となります。$A_i \subseteq B$ だから移行原理より ${}^*A_i \subseteq {}^*B$ となり、従って $\nu(x) \subseteq {}^*B$ となるから $B \in \mathcal{O}$ です。これで $\mathcal{O}$ が開集合系の性質を全てみたすことが示されたので、$X$ に位相が定まります。
この位相に関して近傍系やモナドが定まりますが、$A$ が点 $x$ の近傍ならば簡単な考察により $\nu(x) \subseteq {}^*A$ がわかるので、$\nu(x) \subseteq \mathrm{monad}(x)$ となります。一般には必ずしもこれらは等しくなりません。
この方法を使って位相空間 $X$ を $X \subsetneq Y$ となる集合 $Y$ に拡張することを考えます。このため、一般に一方が他方の部分位相空間となるための超準モデルによる同値条件を考察します。
$X \subseteq Y$ の関係にある位相空間 $X, Y$ がそれぞれあるとします。$X$ と $Y$ の開集合系をそれぞれ $\mathcal{O}_X, \mathcal{O}_Y$ とし、また、$X$ における点 $x$ の近傍系とモナドをそれぞれ $\mathcal{N}_X(x), \mathrm{monad}_X(x)$ とかき、同様に $Y$ における点 $x$ の近傍系とモナドをそれぞれ $\mathcal{N}_Y(x), \mathrm{monad}_Y(x)$ とかくことにします。このとき、$X$ が $Y$ の部分位相空間であるとは、
\begin{equation} \tag{1}
\forall A \in \mathscr{P}(X) \, (A \in \mathcal{O}_X \leftrightarrow \exists B \in \mathcal{O}_Y \, (A = B \cap X))
\end{equation}
であることをいいます。
これを超準モデルでの同値条件で表したものが次の定理です。
【定理1】位相空間 $X,Y$ が $X \subseteq Y$ のとき、$X$ が $Y$ の部分位相空間となることは、
\begin{equation} \tag{2}
\forall x \in X \, (\mathrm{monad}_X(x) = \mathrm{monad}_Y(x) \cap {}^*X)
\end{equation}
が成り立つことと同値である。
(証明)$(1) \Leftrightarrow (2)$ を示せばよい。
$(1) \Rightarrow (2)$ : $(1)$ が成り立つとし、任意に $x \in X$ をとる。
任意に $B \in \mathcal{N}_Y(x)$ をとると、$x \in B' \subseteq B$ となる $B' \in \mathcal{O}_Y$ がとれ、$A' = B' \cap X$ とすると $(1)$ より $A' \in \mathcal{O}_X$ で、$x \in A'$ だから
\begin{equation*}
\mathrm{monad}_X(x) \subseteq {}^*A' \subseteq {}^*B' \subseteq {}^*B
\end{equation*}
である。$B \in \mathcal{N}_Y(x)$ は任意だから $\mathrm{monad}_X(x) \subseteq \mathrm{monad}_Y(x)$ であり、また $\mathrm{monad}_X(x) \subseteq {}^*X$ は明らかだから $\mathrm{monad}_X(x) \subseteq \mathrm{monad}_Y(x) \cap {}^*X$ が得られる。
逆に、任意に $A \in \mathcal{N}_X(x)$ をとると、$x \in A' \subseteq A$ となる $A' \in \mathcal{O}_X$ がとれ、$(1)$ よりある $B' \in \mathcal{O}_Y$ に対して $A' = B' \cap X$ となり、$x \in B'$ だから $\mathrm{monad}_Y(x) \subseteq {}^*B'$ より
\begin{equation*}
\mathrm{monad}_Y(x) \cap {}^*X \subseteq {}^*B' \cap {}^*X = {}^*A' \subseteq {}^*A
\end{equation*}
であり、$A \in \mathcal{N}_X(x)$ は任意だから $\mathrm{monad}_Y(x) \cap {}^*X \subseteq \mathrm{monad}_X(x)$ が得られる。
以上より $\mathrm{monad}_X(x) = \mathrm{monad}_Y(x) \cap {}^*X$ であり、$(2)$ が示された。
$(2) \Rightarrow (1)$ : $(2)$ が成り立つとし、任意に $A \in \mathscr{P}(X)$ をとる。
$A \in \mathcal{O}_X$ とする。$B' = A \cup (Y \setminus X)$ とおき、任意の $x \in A$ に対して $\mathrm{monad}_Y(x) \subseteq {}^*B'$ となることを示す。任意に $y \in \mathrm{monad}_Y(x)$ をとると、$y \in {}^*X$ ならば $(2)$ より
\begin{equation*}
y \in \mathrm{monad}_Y(x) \cap {}^*X = \mathrm{monad}_X(x) \subseteq {}^*A \subseteq {}^*B'
\end{equation*}
となるから $y \in {}^*B'$ である。$y \notin {}^*X$ ならば
\begin{equation*}
y \in {}^*Y \setminus {}^*X = {}^*(Y \setminus X) \subseteq {}^*B'
\end{equation*}
よりやはり $y \in {}^*B'$ である。これで $\mathrm{monad}_Y(x) \subseteq {}^*B'$ が示されたから $B' \in \mathcal{N}_Y(x)$ であり、$x \in B(x) \subseteq B'$ をみたす $B(x) \in \mathcal{O}_Y$ が存在する。$B = \bigcup_{x \in A}B(x)$ とおくと $B \in \mathcal{O}_Y$ かつ $B \subseteq B'$ で、明らかに $A \subseteq B \cap X$ であり、また $B \cap X \subseteq B' \cap X = A$ だから $A = B \cap X$ である。
逆に、ある $B \in \mathcal{O}_Y$ に対して $A = B \cap X$ ならば、任意の $x \in A$ に対して、$\mathrm{monad}_Y(x) \subseteq {}^*B$ と $(2)$ より
\begin{equation*}
\mathrm{monad}_X(x) = \mathrm{monad}_Y(x) \cap {}^*X \subseteq {}^*B \cap {}^*X = {}^*A
\end{equation*}
が得られるから、$A \in \mathcal{O}_X$ である。
以上より $A \in \mathcal{O}_X \leftrightarrow \exists B \in \mathcal{O}_Y \, (A = B \cap X)$ であり、$(1)$ が示された。□
さて、超準モデルを使って位相空間 $X$ を $X \subsetneq Y$ となる $Y$ に拡張する一つの方法を、次の補題によって示します。
【補題2】位相空間 $X$ と $X \subsetneq Y$ となる $Y$ があり、任意の $x \in Y \setminus X$ に対して $x \in \nu(x)$ をみたす $\nu(x) \in \mathscr{P}({}^*X)$ が定まっているとする。このとき任意の $x \in X$ に対して $\nu(x) = \mathrm{monad}_X(x)$ と定め、
\begin{equation*}
\mathcal{O}_Y = \{ \, A \in \mathscr{P}(Y) \, \mid \, \forall x \in A \, (\nu(x) \subseteq {}^*A) \, \}
\end{equation*}
で定まる開集合系 $\mathcal{O}_Y$ によって $Y$ に位相を定めると、
\begin{equation} \tag{3}
\forall x \in X \, (\mathrm{monad}_X(x) = \mathrm{monad}_Y(x))
\end{equation}
であり、従って【定理1】より $X$ は $Y$ の部分位相空間となる。
(証明)
任意に $x \in X$ をとる。まず、$\mathrm{monad}_X(x) = \nu(x) \subseteq \mathrm{monad}_Y(x)$ である。逆の包含関係を示すため、任意に $A \in \mathcal{N}_X(x)$ をとると、$x \in B \subseteq A$ となる $B \in \mathcal{O}_X$ が存在し、$\forall y \in B \, (\nu(y) = \mathrm{monad}_X(y) \subseteq {}^*B)$ より $B \in \mathcal{O}_Y$ となるから $A \in \mathcal{N}_Y(x)$ であり、これより $\mathrm{monad}_Y(x) \subseteq {}^*A$ である。$A \in \mathcal{N}_X(x)$ は任意だから $\mathrm{monad}_Y(x) \subseteq \mathrm{monad}_X(x)$ が得られる。以上で $(3)$ が示された。□
この補題の方法は、本来は $(2)$ でよいのにそれより強い $(3)$ が得られることから、位相空間の拡張手段としてはかなり「雑」といえます。しかし次に示す目的のためには、この方法で十分です。
2. アレクサンドロフの1点コンパクト化
ここまでの考察を利用して、「アレクサンドロフの1点コンパクト化」を超準モデルを用いて構成します。
位相空間 $X$ に対し、$X$ に属さない1点 $\infty$ を $X$ に追加した空間 $Y = X \cup \{ \infty \}$ を考え、次によって $\nu(\infty)$ を定めます。
\begin{equation*}
\nu(\infty) = \{ \, y \in {}^*X \, \mid \, \forall x \in X \, (y \notin \mathrm{monad}_X(x)) \, \} \cup \{ \infty \}
\end{equation*}
つまり「 ${}^*X$ のすべての遠標準点と $\infty$ を集めた集合」を $\nu(\infty)$ と定めます。
これを用いて【補題2】の方法で $X$ を部分位相空間とする $Y$ の位相が定まります。$(3)$ が成立するので、以下 $\mathrm{monad}$ の添字は省略します。
このとき、まず $Y$ はコンパクトです。なぜなら任意に $y \in {}^*Y$ をとると、$y$ はある $x \in X$ に対して $y \in \mathrm{monad}(x)$ となるか、または $y \in \nu(\infty)$ となるかのどちらかで、後者ならば $y \in \nu(\infty) \subseteq \mathrm{monad}(\infty)$ なので、第17回【定理5】より $Y$ はコンパクトになります。
次に、$X$ がコンパクトでない場合、$X$ は $Y$ において稠密となります。なぜなら $X$ がコンパクトでなければ ${}^*X$ は遠標準点をもつから $\nu(\infty) \cap {}^*X \neq \emptyset$ であり、従って $\mathrm{monad}(\infty) \cap {}^*X \neq \emptyset$ より $\forall x \in Y \, ( \mathrm{monad}(x) \cap {}^*X \neq \emptyset )$ となるから、第17回【定理3】の ix) より $X$ は $Y$ において稠密です。
これらの条件をみたす $Y = X \cup \{ \infty \}$ を $X$ のアレクサンドロフの1点コンパクト化といいます。従って上の方法は、任意のコンパクトでない位相空間から1点コンパクト化を構成する(超準モデルを使った)一つの方法を示しています。
さらに次が成り立ちます。
【補題3】$X$ がハウスドルフかつ局所コンパクト(任意の点に対してコンパクトな近傍が存在する)ならば、上の方法で構成した1点コンパクト化において、
\begin{equation*}
\mathrm{monad}(\infty) = \nu(\infty)
\end{equation*}
が成立する。
(証明)
$\mathrm{monad}(\infty) \supseteq \nu(\infty)$ は既に証明済み。$\mathrm{monad}(\infty) \subseteq \nu(\infty)$ を示すため、ある $ y \in \mathrm{monad}(\infty) \setminus \nu(\infty)$ が存在すると仮定して矛盾を導く。$y \notin \nu(\infty)$ なので、$\nu(\infty)$ の定義より、ある $x \in X$ に対して $y \in \mathrm{monad}(x)$ である。$X$ は局所コンパクトだから $A \in \mathcal{N}_X(x)$ となるコンパクトな $A$ が存在して $y \in \mathrm{monad}(x) \subseteq {}^*A$ より $y \in {}^*A$ となる。$X$ はハウスドルフだから第17回【定理6】 ii) より $A$ は $X$ の閉集合で、従って $X \setminus A$ は $X$ の開集合である。そこで $B = (X \setminus A) \cup \{ \infty \}$ とすると $B = Y \setminus A$ で、任意の $z \in X \setminus A$ に対して $\nu(z) = \mathrm{monad}(z) \subseteq {}^*(X \setminus A) \subseteq {}^*B$ である。また $A$ がコンパクトだから第17回【定理5】より ${}^*A$ の点は全て ${}^*X$ の近標準点で、$\nu(\infty)$ は ${}^*X$ の遠標準点と $\infty$ の集合だから $\nu(\infty) \cap {}^*A = \emptyset$ であり、これより $\nu(\infty) \subseteq {}^*Y \setminus {}^*A = {}^*(Y \setminus A) = {}^*B$ となる。従って $B$ は $Y$ における開集合であるから $\infty$ の近傍であり、 $y \in \mathrm{monad}(\infty) \subseteq {}^*B = {}^*Y \setminus {}^*A$ となるから $y \in {}^*A$ と矛盾する。以上より $\mathrm{monad}(\infty) \subseteq \nu(\infty)$ が得られたから $\mathrm{monad}(\infty) = \nu(\infty)$ である。□
この補題を使って、次の有名な結果が示されます。
【定理4】$X$ がハウスドルフかつ局所コンパクトのとき、上の方法で構成した1点コンパクト化はハウスドルフである。
(証明)
$X$ がハウスドルフであることと第17回【定理4】 ii) より、任意の $x, y \in X$ に対して $x \neq y \to \mathrm{monad}(x) \cap \mathrm{monad}(y) = \emptyset$ である。さらに【補題3】より $\mathrm{monad}(x) \cap \mathrm{monad}(\infty) = \mathrm{monad}(x) \cap \nu(\infty) = \emptyset$ も明らかなので、任意の $x, y \in Y$ に対して $x \neq y \to \mathrm{monad}(x) \cap \mathrm{monad}(y) = \emptyset$ が成り立ち、従って再び第17回【定理4】 ii) より $Y$ もハウスドルフである。□
ついでに、この定理の逆も超準モデルを利用して示しておきましょう。そのために必要になるのが次の補題です。
【補題5】位相空間 $X$ が $Y = X \cup \{ \infty \} \ ( \infty \notin X )$ の部分位相空間であり、かつ $Y$ が $\mathrm{T}_1$ ならば、次が成立する。
\begin{equation} \tag{4}
\forall x \in X \, (\mathrm{monad}_X(x) = \mathrm{monad}_Y(x))
\end{equation}
(証明)
【定理1】より任意の $x \in X$ に対して
\begin{equation*}
\mathrm{monad}_X(x) = \mathrm{monad}_Y(x) \cap {}^*X
\end{equation*}
が成立する。$Y$ が $\mathrm{T}_1$ だから第17回【定理4】 i) より $\infty \notin \mathrm{monad}_Y(x)$ であり、かつ ${}^*Y = {}^*X \cup \{ \infty \}$ だから $\mathrm{monad}_Y(x) \subseteq {}^*X$ すなわち $\mathrm{monad}_Y(x) \cap {}^*X = \mathrm{monad}_Y(x)$ である。従って $(4)$ が成立する。□
この補題を使って、【定理4】の逆が次のように示されます。
【定理6】$X$ の1点コンパクト化 $Y$ がハウスドルフならば、$X$ はハウスドルフかつ局所コンパクトである。
(証明)
$Y$ はハウスドルフだから $\mathrm{T}_1$ であり、【補題5】より $(4)$ が成立する。従って $Y$ のハウスドルフ性と第17回【定理4】 ii) より $X$ もハウスドルフである。任意に $x \in X$ をとると、$Y$ がハウスドルフだから $Y$ における $x$ の開近傍 $A$ と $\infty$ の開近傍 $B$ で $A \cap B = \emptyset$ となるものがとれる。$C = Y \setminus B$ とすると、$C$ はコンパクト空間 $Y$ の閉集合だから、第17回【定理6】 i) より $Y$ においてコンパクトである。従って第17回【定理5】より、
\begin{equation*}
\forall y \in {}^*C \, \exists z \in C \, (y \in \mathrm{monad}_Y(z))
\end{equation*}
が成立するが、$\infty \notin C$ より $C \subseteq X$ であり、これと $(4)$ より
\begin{equation*}
\forall y \in {}^*C \, \exists z \in C \, (y \in \mathrm{monad}_X(z))
\end{equation*}
が成立し、第17回【定理5】より $C$ は $X$ においてもコンパクトである。$A \subseteq C$ だから $C$ は $x$ のコンパクトな近傍であり、$x \in X$ は任意だから $X$ は局所コンパクトである。□
以上でアレクサンドロフの1点コンパクト化に関する諸定理が、超準モデルを使って証明されました。通常の方法に比べて特に簡単になるとは言えませんが、ハウスドルフ性やコンパクト性とモナドとの関係を見通しよく利用することができて、面白い方法だと思います。
(続く)(前記事)(目次)
わかってない奴がわかったつもりで書き留める超準解析(その17) [数学]
【超準解析について生半可な知識しかない僕が、わかったつもりの内容をちょっとずつ書き留めていきます。不正確な内容や誤りもあることをご承知ください。】
(17) 位相空間の超準的考察
第7回で距離空間を超準的に考察しましたが、本記事では一般の位相空間を超準的に考察することにします。位相空間の諸概念が簡単な論理式で表現できて、とても面白いです。
1. 上部構造と広大性原理
位相空間を超準的に考察するためには、超準モデルの「広大性原理」と呼ばれる性質が必要となります。まずこれを極めて雑にですが説明します。
$X$ を無限集合とし、適切な無限集合 $I$ とその上の超フィルターを使って、第6回で示した方法を使って $X$ から超冪 ${}^*X$ を構成します。同一視によって $X \subseteq {}^*X$ とみなし、${}^*X$ は $X$ の真の拡大とすることができます。
さらに考察の対象を広げて、$X$ から始めてその冪集合 $\mathscr{P}(X)$ との和集合 $X \cup \mathscr{P}(X)$ を作り、またその冪集合との和集合を作り、この作業を任意有限回繰り返してできる集合すべての和集合を $\mathcal{U}$ とします。これを「 $X$ の上部構造」と呼びます。また、 ${}^*X$ から始めて同様の操作で作られる「 ${}^*X$ の上部構造」を ${}^*\mathcal{U}$ とします。このとき $\mathcal{U}$ から ${}^*\mathcal{U}$ への写像 ${}^*$ を定義し、任意の $a \in \mathcal{U}$ に対して ${}^*a \in {}^*\mathcal{U}$ を対応させることができます。ただし $x \in X$ に対しては ${}^*x = x$ となります。
本稿ではこうして作った ${}^*\mathcal{U}$ を $\mathcal{U}$ の超準モデルとよび、$a$ に対する ${}^*a$ を $a$ の超準拡大とよぶこととします(あまり標準的なよび方ではないかもしれません)。
集合論言語の論理式 $\varphi(x_1, x_2, \cdots , x_n)$( $x_1, x_2, \cdots , x_n$ 以外に自由変数を持たない)と任意の $a_1, a_2, \cdots , a_n \in \mathcal{U}$ に対して、次の移行原理が成り立ちます。
ここでは「有界論理式」についての詳細は省略します。移行原理によって、任意の $X$ の部分集合 $A, B$ に対して、例えば ${}^*(A \cap B) = {}^*A \cap {}^*B$ や $A \subseteq B \Leftrightarrow {}^*A \subseteq {}^*B$ などの法則が示されます(第1回を参照)。
これに加え、超冪の構成で使用する $I$ とその上の超フィルターをうまくとると、次の広大性原理とよばれる性質が成り立ちます。
本記事では、超準モデルでは常に広大性原理が成立するものとします。
2. 位相空間の基本概念の超準的考察
$\langle X, \mathcal{O} \rangle$ を無限個の元をもつ位相空間とします。$\mathcal{O}$ は開集合系で、以降これを簡単に「位相空間 $X$」と呼びます。$x \in X, A \in \mathscr{P}(X)$ に対して $A$ が $x$ の近傍であるとは、$x \in B \subseteq A$ となる開集合 $B$ が存在することです。$x \in X$ に対して $x$ の近傍の全体を $\mathcal{N}(x)$ とかくこととします。
ここで、超準モデルを使ってモナドと呼ばれる次の集合を定義します。
必ず $x \in \mathrm{monad}(x)$ なので、これは空集合にはなりません。このとき次が成立します。
(証明)
$\Rightarrow$ の証明:モナドの定義から明らか。
$\Leftarrow$ の証明:$\mathrm{monad}(x) \subseteq {}^*A$ とし、$A \notin \mathcal{N}(x)$ を仮定して矛盾を導く。このとき任意の $B \in \mathcal{N}(x)$ に対して $B \not\subseteq A$ であるから $\exists y \in X \, (y \in B \setminus A)$ である。そこで、$\mathcal{N}(x) \times X$ 上の関係 $R$ を
\begin{equation*}
R = \{ \, \langle B, y \rangle \in \mathcal{N}(x) \times X \, \mid \, y \in B \setminus A \, \}
\end{equation*}
によって定めると、任意有限個の $B_1, B_2, \cdots , B_n \in \mathcal{N}(x)$ に対して $B_1 \cap B_2 \cap \cdots \cap B_n \in \mathcal{N}(x)$ だから、
\begin{equation*}
\exists y \in X \, (\langle B_1, y \rangle \in R \land \langle B_2, y \rangle \in R \land \cdots \land \langle B_n, y \rangle \in R)
\end{equation*}
が成り立ち、$R$ は有限共起的である。従って広大性原理によって
\begin{equation*}
\exists y \in {}^*X \, \forall B \in \mathcal{N}(x) \, (\langle {}^*B, y \rangle \in {}^*R)
\end{equation*}
すなわち
\begin{equation*}
\exists y \in {}^*X \, \forall B \in \mathcal{N}(x) \, (y \in {}^*B \setminus {}^*A)
\end{equation*}
が成り立つ。これより
\begin{equation*}
\exists y \in {}^*X \, (y \in \mathrm{monad}(x) \setminus {}^*A)
\end{equation*}
が従い、これは $\mathrm{monad}(x) \not\subseteq {}^*A$ を意味するから矛盾である。□
これを基本として、位相空間の様々な概念を超準モデルの論理式で表すことができます。
(証明)
i) $A$ が開集合 $\quad \Leftrightarrow \quad A$ が $A$ の各点 $x$ の近傍
$\quad \Leftrightarrow \quad \forall x \in A \, (\mathrm{monad}(x) \subseteq {}^*A)$
ii) $A$ が閉集合 $\quad \Leftrightarrow \quad X \setminus A$ が開集合
$\quad \Leftrightarrow \quad \forall x \in X \setminus A \, (\mathrm{monad}(x) \subseteq {}^*X \setminus {}^*A)$
$\quad \Leftrightarrow \quad \forall x \in X \, (x \notin A \to \mathrm{monad}(x) \cap {}^*A = \emptyset)$
$\quad \Leftrightarrow \quad \forall x \in X \, (\mathrm{monad}(x) \cap {}^*A \neq \emptyset \to x \in A)$
iii) $x$ が $A$ の内点 $\quad \Leftrightarrow \quad A$ が $x$ の近傍 $\quad \Leftrightarrow \quad \mathrm{monad}(x) \subseteq {}^*A$
iv) $x$ が $A$ の触点 $\quad \Leftrightarrow \quad x$ が $X \setminus A$ の内点でない $\quad \Leftrightarrow \quad \mathrm{monad}(x) \not\subseteq {}^*X \setminus {}^*A$
$\quad \Leftrightarrow \quad \mathrm{monad}(x) \cap {}^*A \neq \emptyset$
v) $x$ が $A$ の境界点 $\quad \Leftrightarrow \quad x$ が $A$ と $X \setminus A$ の両方の触点
$\quad \Leftrightarrow \quad \mathrm{monad}(x) \cap {}^*A \neq \emptyset \land \mathrm{monad}(x) \cap ({}^*X \setminus {}^*A) \neq \emptyset$
vi) $x$ が $A$ の孤立点 $\quad \Leftrightarrow \quad \exists B \in \mathcal{N}(x) \, (B \cap A = \{ x \} )$
$\quad \Leftrightarrow \quad \exists B \in \mathcal{N}(x) \, (B \subseteq (X \setminus A) \cup \{ x \} \land x \in A)$
$\quad \Leftrightarrow \quad \exists B \in \mathcal{N}(x) \, ({}^*B \subseteq ({}^*X \setminus {}^*A) \cup \{ x \} \land x \in {}^*A)$ (移行原理)
$\quad \Leftrightarrow \quad \exists B \in \mathscr{P}(X) \, (\mathrm{monad}(x) \subseteq {}^*B \subseteq ({}^*X \setminus {}^*A) \cup \{ x \} \land x \in {}^*A)$
$\quad \Leftrightarrow \quad \mathrm{monad}(x) \subseteq ({}^*X \setminus {}^*A) \cup \{ x \} \land x \in {}^*A$
$\quad \Leftrightarrow \quad \mathrm{monad}(x) \cap {}^*A = \{ x \}$
vii) $x$ が $A$ の集積点 $\quad \Leftrightarrow \quad$ $x$ が $A$ の触点であり、かつ孤立点でない
$\quad \Leftrightarrow \quad \mathrm{monad}(x) \cap {}^*A \neq \emptyset \land \mathrm{monad}(x) \cap {}^*A \neq \{ x \}$
$\quad \Leftrightarrow \quad ( \mathrm{monad}(x) \cap {}^*A) \setminus \{ x \} \neq \emptyset$
viii) $A$ が自己稠密 $\quad \Leftrightarrow \quad A$ の各点が $A$ の集積点
$\quad \Leftrightarrow \quad \forall x \in A \, ( ( \mathrm{monad}(x) \cap {}^*A) \setminus \{ x \} \neq \emptyset )$
ix) $A$ が $X$ において稠密 $\quad \Leftrightarrow \quad X$ の各点が $A$ の触点
$\quad \Leftrightarrow \quad \forall x \in X \, ( \mathrm{monad}(x) \cap {}^*A \neq \emptyset )$
□
【定理3】の表の論理式は、第7回で紹介した距離空間における表の右側欄と同じになっていることがわかります。距離空間は位相空間の特別なものなので、この結果は整合が取れています。
3. 分離公理とコンパクト性
2種類の分離公理について、超準モデルによる同値条件を示します。
(証明)
i) $X$ が $\mathrm{T}_1$ である
$\quad \Leftrightarrow \quad \forall x, y \in X \, (x \neq y \to \exists A \in \mathcal{N}(x) \, (y \notin A) \land \exists B \in \mathcal{N}(y) \, (x \notin B))$
$\quad \Leftrightarrow \quad \forall x, y \in X \, (x \neq y \to \exists A \in \mathcal{N}(x) \, (y \notin {}^*A) \land \exists B \in \mathcal{N}(y) \, (x \notin {}^*B))$ (移行原理)
$\quad \Leftrightarrow \quad \forall x, y \in X \, (x \neq y \to y \notin \mathrm{monad}(x) \land x \notin \mathrm{monad}(y))$
ii) $X$ が $\mathrm{T}_2$(ハウスドルフ)である
$\quad \Leftrightarrow \quad \forall x, y \in X \, (x \neq y \to \exists A \in \mathcal{N}(x) \, \exists B \in \mathcal{N}(y) \, (A \cap B = \emptyset))$
$\quad \Leftrightarrow \quad \forall x, y \in X \, (x \neq y \to \exists A \in \mathcal{N}(x) \, \exists B \in \mathcal{N}(y) \, ({}^*A \cap {}^*B = \emptyset))$ (移行原理)
$\quad \Rightarrow \quad \forall x, y \in X \, (x \neq y \to \mathrm{monad}(x) \cap \mathrm{monad}(y) = \emptyset )$
逆に $\forall x, y \in X \, (x \neq y \to \mathrm{monad}(x) \cap \mathrm{monad}(y) = \emptyset )$ かつ $X$ がハウスドルフでないと仮定すると、ある $x, y \in X, x \neq y$ が存在して、
\begin{equation*}
\forall A \in \mathcal{N}(x) \, \forall B \in \mathcal{N}(y) \, (A \cap B \neq \emptyset))
\end{equation*}
すなわち
\begin{equation*}
\forall A \in \mathcal{N}(x) \, \forall B \in \mathcal{N}(y) \, \exists z \in X \, (z \in A \cap B)
\end{equation*}
となる。そこで $(\mathcal{N}(x) \times \mathcal{N}(y)) \times X$ 上の関係 $R$ を、
\begin{equation*}
R = \{ \, \langle \langle A, B \rangle , z \rangle \in (\mathcal{N}(x) \times \mathcal{N}(y)) \times X \, \mid \, z \in A \cap B \, \}
\end{equation*}
によって定めると、$R$ は明らかに有限共起的だから、広大性原理によって、
\begin{equation*}
\exists z \in {}^*X \, \forall A \in \mathcal{N}(x) \, \forall B \in \mathcal{N}(y) \, (z \in {}^*A \cap {}^*B)
\end{equation*}
が成り立つ。よって $\exists z \in {}^*X \, (z \in \mathrm{monad}(x) \cap \mathrm{monad}(y))$ となるが、これは $\mathrm{monad}(x) \cap \mathrm{monad}(y) = \emptyset$ と矛盾する。よって、
$\forall x, y \in X \, (x \neq y \to \mathrm{monad}(x) \cap \mathrm{monad}(y) = \emptyset ) \quad \Rightarrow \quad X$ が$\mathrm{T}_2$(ハウスドルフ)である
□
この定理より、$\mathrm{T}_1$ 空間は「どの点も他の点のモナドに属さない空間」、ハウスドルフ空間は「異なる点のモナドが交わらない空間」とイメージできます。特にハウスドルフ空間を簡単に言うと「モナドがダブらない空間」です。
また、コンパクト性については、次の非常に簡明な同値条件があります。
(証明)
$\Rightarrow$ の証明:$A$ がコンパクトとする。$\exists y \in {}^*A \, \forall x \in A \, (y \notin \mathrm{monad}(x))$ を仮定して矛盾を導く。これをみたす $y$ をとると、任意の $x \in A$ に対して開近傍 $B(x) \in \mathcal{N}(x) \cap \mathcal{O}$ が存在して $y \notin {}^*B(x)$ となる。すると、
\begin{equation*}
\{ \, B(x) \, \mid \, x \in A \, \}
\end{equation*}
は $A$ の開被覆であり、$A$ はコンパクトだから有限個の $x_1, x_2, \cdots , x_n$ がとれて、
\begin{equation*}
A \subseteq B(x_1) \cup B(x_2) \cup \cdots \cup B(x_n)
\end{equation*}
とすることができる。移行原理より、
\begin{equation*}
{}^*A \subseteq {}^*B(x_1) \cup {}^*B(x_2) \cup \cdots \cup {}^*B(x_n)
\end{equation*}
かつ $y \notin {}^*B(x_1) \cup {}^*B(x_2) \cup \cdots \cup {}^*B(x_n)$ だから $y \notin {}^*A$ となるが、これは矛盾である。
$\Leftarrow$ の証明:$\forall y \in {}^*A \, \exists x \in A \, (y \in \mathrm{monad}(x))$ とする。$A$ がコンパクトでないと仮定して矛盾を導く。$A$ の開被覆 $\mathcal{C}$ で、有限個の元をどのようにとっても $A$ の被覆にならないものが存在する。このとき $\mathcal{C} \times A$ 上の関係 $R$ を、
\begin{equation*}
R = \{ \, \langle B, y \rangle \in \mathcal{C} \times A \, \mid \, y \notin B \, \}
\end{equation*}
によって定めると、任意有限個の $B_1, B_2, \cdots , B_n \in \mathcal{C}$ に対して $A \setminus (B_1 \cup B_2 \cup \cdots \cup B_n) \neq \emptyset$ だから、
\begin{equation*}
\exists y \in A \, (\langle B_1, y \rangle \in R \land \langle B_2, y \rangle \in R \land \cdots \land \langle B_n, y \rangle \in R)
\end{equation*}
となって $R$ は有限共起的である。従って広大性原理より、
\begin{equation*}
\exists y \in {}^*A \, \forall B \in \mathcal{C} \, (\langle {}^*B, y \rangle \in {}^*R)
\end{equation*}
すなわち
\begin{equation*}
\exists y \in {}^*A \, \forall B \in \mathcal{C} \, (y \notin {}^*B)
\end{equation*}
である。これをみたす $y$ をとると、$y \in \mathrm{monad}(x)$ となる $x \in A$ が存在し、この $x$ に対し $x \in B_0 \in \mathcal{C}$ となる開集合 $B_0$ が存在するから、
\begin{equation*}
y \in \mathrm{monad}(x) \subseteq {}^*B_0
\end{equation*}
すなわち $y \in {}^*B_0$ となるが、一方で $\forall B \in \mathcal{C} \, (y \notin {}^*B)$ より $y \notin {}^*B_0$ だから矛盾である。□
この定理より、コンパクト集合は「超準拡大が各点のモナドで覆い切れる集合」とイメージできます。もっと簡単に言うと「モナドに漏れがない集合」です。この結果も第8回の距離空間に関する結果と整合が取れていることがわかります。
そうすると、ハウスドルフでかつコンパクトな位相空間は「モナドにダブリも漏れもない空間」、どこかで聞いた用語を使うと「モナドがMECEな空間」となります。イメージしやすいですね。
これらの同値条件を使うと、例えば次の定理が論理式を使った簡単な考察だけで証明できます。
(証明)
i) 任意に $y \in {}^*A$ をとる。$X$ がコンパクトだから【定理5】より $y \in \mathrm{monad}(x)$ となる $x \in X$ が存在する。$y \in \mathrm{monad}(x) \cap {}^*A$ すなわち $\mathrm{monad}(x) \cap {}^*A \neq \emptyset$ で、$A$ は閉集合だから、【定理3】ii) より $x \in A$ となる。従って $\forall y \in {}^*A \, \exists x \in A \, (y \in \mathrm{monad}(x))$ であるから、再び【定理5】より $A$ はコンパクトである。
ii) 任意に $\mathrm{monad}(x) \cap {}^*A \neq \emptyset$ をみたす $x \in X$ をとる。$y \in \mathrm{monad}(x) \cap {}^*A$ をとると、$A$ がコンパクトだから【定理5】より $y \in \mathrm{monad}(x')$ となる $x' \in A$ がある。$\mathrm{monad}(x) \cap \mathrm{monad}(x') \neq \emptyset$ で $X$ がハウスドルフだから、【定理4】ii) より $x = x'$ であり、これより $x \in A$ となる。従って【定理3】ii) より $A$ は閉集合である。
□
なお、$\exists x \in X \, (y \in \mathrm{monad}(x))$ をみたす $y \in {}^*X$ を ${}^*X$ の近標準点といい、そうでない $y \in {}^*X$ を ${}^*X$ の遠標準点といいます。この用語を使うと、空間 $X$ 自身がコンパクトであることは「すべての ${}^*X$ の点が近標準点である」ことと同値です。
[参考文献]
中村 徹『超準解析と物理学(増補改訂版)』(日本評論社, 2017)
(続く)(前記事)(目次)
(17) 位相空間の超準的考察
第7回で距離空間を超準的に考察しましたが、本記事では一般の位相空間を超準的に考察することにします。位相空間の諸概念が簡単な論理式で表現できて、とても面白いです。
1. 上部構造と広大性原理
位相空間を超準的に考察するためには、超準モデルの「広大性原理」と呼ばれる性質が必要となります。まずこれを極めて雑にですが説明します。
$X$ を無限集合とし、適切な無限集合 $I$ とその上の超フィルターを使って、第6回で示した方法を使って $X$ から超冪 ${}^*X$ を構成します。同一視によって $X \subseteq {}^*X$ とみなし、${}^*X$ は $X$ の真の拡大とすることができます。
さらに考察の対象を広げて、$X$ から始めてその冪集合 $\mathscr{P}(X)$ との和集合 $X \cup \mathscr{P}(X)$ を作り、またその冪集合との和集合を作り、この作業を任意有限回繰り返してできる集合すべての和集合を $\mathcal{U}$ とします。これを「 $X$ の上部構造」と呼びます。また、 ${}^*X$ から始めて同様の操作で作られる「 ${}^*X$ の上部構造」を ${}^*\mathcal{U}$ とします。このとき $\mathcal{U}$ から ${}^*\mathcal{U}$ への写像 ${}^*$ を定義し、任意の $a \in \mathcal{U}$ に対して ${}^*a \in {}^*\mathcal{U}$ を対応させることができます。ただし $x \in X$ に対しては ${}^*x = x$ となります。
本稿ではこうして作った ${}^*\mathcal{U}$ を $\mathcal{U}$ の超準モデルとよび、$a$ に対する ${}^*a$ を $a$ の超準拡大とよぶこととします(あまり標準的なよび方ではないかもしれません)。
集合論言語の論理式 $\varphi(x_1, x_2, \cdots , x_n)$( $x_1, x_2, \cdots , x_n$ 以外に自由変数を持たない)と任意の $a_1, a_2, \cdots , a_n \in \mathcal{U}$ に対して、次の移行原理が成り立ちます。
【移行原理】
$\varphi(x_1, x_2, \cdots , x_n)$ が有界論理式のとき、$\mathcal{U}$ 上で \begin{equation*} \varphi(a_1, a_2, \cdots , a_n) \end{equation*} が成り立つことと、${}^*\mathcal{U}$ 上で \begin{equation*} \varphi({}^*a_1, {}^*a_2, \cdots , {}^*a_n) \end{equation*} が成り立つことは同値である。
$\varphi(x_1, x_2, \cdots , x_n)$ が有界論理式のとき、$\mathcal{U}$ 上で \begin{equation*} \varphi(a_1, a_2, \cdots , a_n) \end{equation*} が成り立つことと、${}^*\mathcal{U}$ 上で \begin{equation*} \varphi({}^*a_1, {}^*a_2, \cdots , {}^*a_n) \end{equation*} が成り立つことは同値である。
ここでは「有界論理式」についての詳細は省略します。移行原理によって、任意の $X$ の部分集合 $A, B$ に対して、例えば ${}^*(A \cap B) = {}^*A \cap {}^*B$ や $A \subseteq B \Leftrightarrow {}^*A \subseteq {}^*B$ などの法則が示されます(第1回を参照)。
これに加え、超冪の構成で使用する $I$ とその上の超フィルターをうまくとると、次の広大性原理とよばれる性質が成り立ちます。
【広大性原理】
$\mathcal{U}$ 上の2項関係 $R \, (\subseteq A \times B, \ A, B \in \mathcal{U})$ が有限共起的であるとする。すなわち任意にとった有限個の $a_1, a_2, \cdots , a_n \in \mathrm{Dom}(R) \subseteq A$ に対して、$\mathcal{U}$ 上で \begin{equation*} \exists b \in B \, (\langle a_1, b \rangle \in R \land \langle a_2, b \rangle \in R \land \cdots \land \langle a_n, b \rangle \in R) \end{equation*} が成り立つとする。このとき ${}^*\mathcal{U}$ 上で次が成り立つ。 \begin{equation*} \exists b \in {}^*B \, \forall a \in \mathrm{Dom}(R) \, (\langle {}^*a, b \rangle \in {}^*R) \end{equation*}
$\mathcal{U}$ 上の2項関係 $R \, (\subseteq A \times B, \ A, B \in \mathcal{U})$ が有限共起的であるとする。すなわち任意にとった有限個の $a_1, a_2, \cdots , a_n \in \mathrm{Dom}(R) \subseteq A$ に対して、$\mathcal{U}$ 上で \begin{equation*} \exists b \in B \, (\langle a_1, b \rangle \in R \land \langle a_2, b \rangle \in R \land \cdots \land \langle a_n, b \rangle \in R) \end{equation*} が成り立つとする。このとき ${}^*\mathcal{U}$ 上で次が成り立つ。 \begin{equation*} \exists b \in {}^*B \, \forall a \in \mathrm{Dom}(R) \, (\langle {}^*a, b \rangle \in {}^*R) \end{equation*}
本記事では、超準モデルでは常に広大性原理が成立するものとします。
2. 位相空間の基本概念の超準的考察
$\langle X, \mathcal{O} \rangle$ を無限個の元をもつ位相空間とします。$\mathcal{O}$ は開集合系で、以降これを簡単に「位相空間 $X$」と呼びます。$x \in X, A \in \mathscr{P}(X)$ に対して $A$ が $x$ の近傍であるとは、$x \in B \subseteq A$ となる開集合 $B$ が存在することです。$x \in X$ に対して $x$ の近傍の全体を $\mathcal{N}(x)$ とかくこととします。
ここで、超準モデルを使ってモナドと呼ばれる次の集合を定義します。
【定義1】(モナド)
$x \in X$ に対し、次によって定まる $^*X$ の部分集合 $\mathrm{monad}(x)$ を「$x$ のモナド」と呼ぶ。 \begin{equation*} \mathrm{monad}(x) = \bigcap \{ \, {}^*A \, \mid \, A \in \mathcal{N}(x) \, \} \end{equation*}
$x \in X$ に対し、次によって定まる $^*X$ の部分集合 $\mathrm{monad}(x)$ を「$x$ のモナド」と呼ぶ。 \begin{equation*} \mathrm{monad}(x) = \bigcap \{ \, {}^*A \, \mid \, A \in \mathcal{N}(x) \, \} \end{equation*}
必ず $x \in \mathrm{monad}(x)$ なので、これは空集合にはなりません。このとき次が成立します。
【定理2】(近傍の超準モデルによる同値条件)
$x \in X, A \in \mathscr{P}(X)$ に対して、次が成立する。 \begin{equation*} A \in \mathcal{N}(x) \quad \Leftrightarrow \quad \mathrm{monad}(x) \subseteq {}^*A \end{equation*}
$x \in X, A \in \mathscr{P}(X)$ に対して、次が成立する。 \begin{equation*} A \in \mathcal{N}(x) \quad \Leftrightarrow \quad \mathrm{monad}(x) \subseteq {}^*A \end{equation*}
(証明)
$\Rightarrow$ の証明:モナドの定義から明らか。
$\Leftarrow$ の証明:$\mathrm{monad}(x) \subseteq {}^*A$ とし、$A \notin \mathcal{N}(x)$ を仮定して矛盾を導く。このとき任意の $B \in \mathcal{N}(x)$ に対して $B \not\subseteq A$ であるから $\exists y \in X \, (y \in B \setminus A)$ である。そこで、$\mathcal{N}(x) \times X$ 上の関係 $R$ を
\begin{equation*}
R = \{ \, \langle B, y \rangle \in \mathcal{N}(x) \times X \, \mid \, y \in B \setminus A \, \}
\end{equation*}
によって定めると、任意有限個の $B_1, B_2, \cdots , B_n \in \mathcal{N}(x)$ に対して $B_1 \cap B_2 \cap \cdots \cap B_n \in \mathcal{N}(x)$ だから、
\begin{equation*}
\exists y \in X \, (\langle B_1, y \rangle \in R \land \langle B_2, y \rangle \in R \land \cdots \land \langle B_n, y \rangle \in R)
\end{equation*}
が成り立ち、$R$ は有限共起的である。従って広大性原理によって
\begin{equation*}
\exists y \in {}^*X \, \forall B \in \mathcal{N}(x) \, (\langle {}^*B, y \rangle \in {}^*R)
\end{equation*}
すなわち
\begin{equation*}
\exists y \in {}^*X \, \forall B \in \mathcal{N}(x) \, (y \in {}^*B \setminus {}^*A)
\end{equation*}
が成り立つ。これより
\begin{equation*}
\exists y \in {}^*X \, (y \in \mathrm{monad}(x) \setminus {}^*A)
\end{equation*}
が従い、これは $\mathrm{monad}(x) \not\subseteq {}^*A$ を意味するから矛盾である。□
これを基本として、位相空間の様々な概念を超準モデルの論理式で表すことができます。
【定理3】(位相空間の諸概念の超準モデルによる同値条件)
$x \in X, A \in \mathscr{P}(X)$ に対して、次表の同値な対応関係が成立する。
$x \in X, A \in \mathscr{P}(X)$ に対して、次表の同値な対応関係が成立する。
| 位相的概念 | 超準モデル上の同値条件 | |
|---|---|---|
| i) | $A$ が開集合 | $\forall x \in A \, (\mathrm{monad}(x) \subseteq {}^*A)$ |
| ii) | $A$ が閉集合 | $\forall x \in X \, (\mathrm{monad}(x) \cap {}^*A \neq \emptyset \to x \in A)$ |
| iii) | $x$ が $A$ の内点 | $\mathrm{monad}(x) \subseteq {}^*A$ |
| iv) | $x$ が $A$ の触点 | $\mathrm{monad}(x) \cap {}^*A \neq \emptyset$ |
| v) | $x$ が $A$ の境界点 | $\mathrm{monad}(x) \cap {}^*A \neq \emptyset \land \mathrm{monad}(x) \cap ({}^*X \setminus {}^*A) \neq \emptyset$ |
| vi) | $x$ が $A$ の孤立点 | $\mathrm{monad}(x) \cap {}^*A = \{ x \}$ |
| vii) | $x$ が $A$ の集積点 | $(\mathrm{monad}(x) \cap {}^*A) \setminus \{x\} \neq \emptyset$ |
| viii) | $A$ が自己稠密 | $\forall x \in A \, ((\mathrm{monad}(x) \cap {}^*A) \setminus \{x\} \neq \emptyset)$ |
| ix) | $A$ が $X$ において稠密 | $\forall x \in X \, (\mathrm{monad}(x) \cap {}^*A \neq \emptyset)$ |
(証明)
i) $A$ が開集合 $\quad \Leftrightarrow \quad A$ が $A$ の各点 $x$ の近傍
$\quad \Leftrightarrow \quad \forall x \in A \, (\mathrm{monad}(x) \subseteq {}^*A)$
ii) $A$ が閉集合 $\quad \Leftrightarrow \quad X \setminus A$ が開集合
$\quad \Leftrightarrow \quad \forall x \in X \setminus A \, (\mathrm{monad}(x) \subseteq {}^*X \setminus {}^*A)$
$\quad \Leftrightarrow \quad \forall x \in X \, (x \notin A \to \mathrm{monad}(x) \cap {}^*A = \emptyset)$
$\quad \Leftrightarrow \quad \forall x \in X \, (\mathrm{monad}(x) \cap {}^*A \neq \emptyset \to x \in A)$
iii) $x$ が $A$ の内点 $\quad \Leftrightarrow \quad A$ が $x$ の近傍 $\quad \Leftrightarrow \quad \mathrm{monad}(x) \subseteq {}^*A$
iv) $x$ が $A$ の触点 $\quad \Leftrightarrow \quad x$ が $X \setminus A$ の内点でない $\quad \Leftrightarrow \quad \mathrm{monad}(x) \not\subseteq {}^*X \setminus {}^*A$
$\quad \Leftrightarrow \quad \mathrm{monad}(x) \cap {}^*A \neq \emptyset$
v) $x$ が $A$ の境界点 $\quad \Leftrightarrow \quad x$ が $A$ と $X \setminus A$ の両方の触点
$\quad \Leftrightarrow \quad \mathrm{monad}(x) \cap {}^*A \neq \emptyset \land \mathrm{monad}(x) \cap ({}^*X \setminus {}^*A) \neq \emptyset$
vi) $x$ が $A$ の孤立点 $\quad \Leftrightarrow \quad \exists B \in \mathcal{N}(x) \, (B \cap A = \{ x \} )$
$\quad \Leftrightarrow \quad \exists B \in \mathcal{N}(x) \, (B \subseteq (X \setminus A) \cup \{ x \} \land x \in A)$
$\quad \Leftrightarrow \quad \exists B \in \mathcal{N}(x) \, ({}^*B \subseteq ({}^*X \setminus {}^*A) \cup \{ x \} \land x \in {}^*A)$ (移行原理)
$\quad \Leftrightarrow \quad \exists B \in \mathscr{P}(X) \, (\mathrm{monad}(x) \subseteq {}^*B \subseteq ({}^*X \setminus {}^*A) \cup \{ x \} \land x \in {}^*A)$
$\quad \Leftrightarrow \quad \mathrm{monad}(x) \subseteq ({}^*X \setminus {}^*A) \cup \{ x \} \land x \in {}^*A$
$\quad \Leftrightarrow \quad \mathrm{monad}(x) \cap {}^*A = \{ x \}$
vii) $x$ が $A$ の集積点 $\quad \Leftrightarrow \quad$ $x$ が $A$ の触点であり、かつ孤立点でない
$\quad \Leftrightarrow \quad \mathrm{monad}(x) \cap {}^*A \neq \emptyset \land \mathrm{monad}(x) \cap {}^*A \neq \{ x \}$
$\quad \Leftrightarrow \quad ( \mathrm{monad}(x) \cap {}^*A) \setminus \{ x \} \neq \emptyset$
viii) $A$ が自己稠密 $\quad \Leftrightarrow \quad A$ の各点が $A$ の集積点
$\quad \Leftrightarrow \quad \forall x \in A \, ( ( \mathrm{monad}(x) \cap {}^*A) \setminus \{ x \} \neq \emptyset )$
ix) $A$ が $X$ において稠密 $\quad \Leftrightarrow \quad X$ の各点が $A$ の触点
$\quad \Leftrightarrow \quad \forall x \in X \, ( \mathrm{monad}(x) \cap {}^*A \neq \emptyset )$
□
【定理3】の表の論理式は、第7回で紹介した距離空間における表の右側欄と同じになっていることがわかります。距離空間は位相空間の特別なものなので、この結果は整合が取れています。
3. 分離公理とコンパクト性
2種類の分離公理について、超準モデルによる同値条件を示します。
【定理4】($\mathrm{T}_1, \mathrm{T}_2$ 分離公理の超準モデルによる同値条件)
i) $X$ が $\mathrm{T}_1$ である $\quad \Leftrightarrow \quad \forall x, y \in X \, (x \neq y \to y \notin \mathrm{monad}(x) \land x \notin \mathrm{monad}(y))$
ii) $X$ が $\mathrm{T}_2$(ハウスドルフ)である $\quad \Leftrightarrow \quad \forall x, y \in X \, (x \neq y \to \mathrm{monad}(x) \cap \mathrm{monad}(y) = \emptyset )$
i) $X$ が $\mathrm{T}_1$ である $\quad \Leftrightarrow \quad \forall x, y \in X \, (x \neq y \to y \notin \mathrm{monad}(x) \land x \notin \mathrm{monad}(y))$
ii) $X$ が $\mathrm{T}_2$(ハウスドルフ)である $\quad \Leftrightarrow \quad \forall x, y \in X \, (x \neq y \to \mathrm{monad}(x) \cap \mathrm{monad}(y) = \emptyset )$
(証明)
i) $X$ が $\mathrm{T}_1$ である
$\quad \Leftrightarrow \quad \forall x, y \in X \, (x \neq y \to \exists A \in \mathcal{N}(x) \, (y \notin A) \land \exists B \in \mathcal{N}(y) \, (x \notin B))$
$\quad \Leftrightarrow \quad \forall x, y \in X \, (x \neq y \to \exists A \in \mathcal{N}(x) \, (y \notin {}^*A) \land \exists B \in \mathcal{N}(y) \, (x \notin {}^*B))$ (移行原理)
$\quad \Leftrightarrow \quad \forall x, y \in X \, (x \neq y \to y \notin \mathrm{monad}(x) \land x \notin \mathrm{monad}(y))$
ii) $X$ が $\mathrm{T}_2$(ハウスドルフ)である
$\quad \Leftrightarrow \quad \forall x, y \in X \, (x \neq y \to \exists A \in \mathcal{N}(x) \, \exists B \in \mathcal{N}(y) \, (A \cap B = \emptyset))$
$\quad \Leftrightarrow \quad \forall x, y \in X \, (x \neq y \to \exists A \in \mathcal{N}(x) \, \exists B \in \mathcal{N}(y) \, ({}^*A \cap {}^*B = \emptyset))$ (移行原理)
$\quad \Rightarrow \quad \forall x, y \in X \, (x \neq y \to \mathrm{monad}(x) \cap \mathrm{monad}(y) = \emptyset )$
逆に $\forall x, y \in X \, (x \neq y \to \mathrm{monad}(x) \cap \mathrm{monad}(y) = \emptyset )$ かつ $X$ がハウスドルフでないと仮定すると、ある $x, y \in X, x \neq y$ が存在して、
\begin{equation*}
\forall A \in \mathcal{N}(x) \, \forall B \in \mathcal{N}(y) \, (A \cap B \neq \emptyset))
\end{equation*}
すなわち
\begin{equation*}
\forall A \in \mathcal{N}(x) \, \forall B \in \mathcal{N}(y) \, \exists z \in X \, (z \in A \cap B)
\end{equation*}
となる。そこで $(\mathcal{N}(x) \times \mathcal{N}(y)) \times X$ 上の関係 $R$ を、
\begin{equation*}
R = \{ \, \langle \langle A, B \rangle , z \rangle \in (\mathcal{N}(x) \times \mathcal{N}(y)) \times X \, \mid \, z \in A \cap B \, \}
\end{equation*}
によって定めると、$R$ は明らかに有限共起的だから、広大性原理によって、
\begin{equation*}
\exists z \in {}^*X \, \forall A \in \mathcal{N}(x) \, \forall B \in \mathcal{N}(y) \, (z \in {}^*A \cap {}^*B)
\end{equation*}
が成り立つ。よって $\exists z \in {}^*X \, (z \in \mathrm{monad}(x) \cap \mathrm{monad}(y))$ となるが、これは $\mathrm{monad}(x) \cap \mathrm{monad}(y) = \emptyset$ と矛盾する。よって、
$\forall x, y \in X \, (x \neq y \to \mathrm{monad}(x) \cap \mathrm{monad}(y) = \emptyset ) \quad \Rightarrow \quad X$ が$\mathrm{T}_2$(ハウスドルフ)である
□
この定理より、$\mathrm{T}_1$ 空間は「どの点も他の点のモナドに属さない空間」、ハウスドルフ空間は「異なる点のモナドが交わらない空間」とイメージできます。特にハウスドルフ空間を簡単に言うと「モナドがダブらない空間」です。
また、コンパクト性については、次の非常に簡明な同値条件があります。
【定理5】(コンパクト性の超準モデルによる同値条件)
$A \subseteq X$ とすると、次が成立する。
$A \subseteq X$ とすると、次が成立する。
$A$ がコンパクトである $\quad \Leftrightarrow \quad \forall y \in {}^*A \, \exists x \in A \, (y \in \mathrm{monad}(x))$
(証明)
$\Rightarrow$ の証明:$A$ がコンパクトとする。$\exists y \in {}^*A \, \forall x \in A \, (y \notin \mathrm{monad}(x))$ を仮定して矛盾を導く。これをみたす $y$ をとると、任意の $x \in A$ に対して開近傍 $B(x) \in \mathcal{N}(x) \cap \mathcal{O}$ が存在して $y \notin {}^*B(x)$ となる。すると、
\begin{equation*}
\{ \, B(x) \, \mid \, x \in A \, \}
\end{equation*}
は $A$ の開被覆であり、$A$ はコンパクトだから有限個の $x_1, x_2, \cdots , x_n$ がとれて、
\begin{equation*}
A \subseteq B(x_1) \cup B(x_2) \cup \cdots \cup B(x_n)
\end{equation*}
とすることができる。移行原理より、
\begin{equation*}
{}^*A \subseteq {}^*B(x_1) \cup {}^*B(x_2) \cup \cdots \cup {}^*B(x_n)
\end{equation*}
かつ $y \notin {}^*B(x_1) \cup {}^*B(x_2) \cup \cdots \cup {}^*B(x_n)$ だから $y \notin {}^*A$ となるが、これは矛盾である。
$\Leftarrow$ の証明:$\forall y \in {}^*A \, \exists x \in A \, (y \in \mathrm{monad}(x))$ とする。$A$ がコンパクトでないと仮定して矛盾を導く。$A$ の開被覆 $\mathcal{C}$ で、有限個の元をどのようにとっても $A$ の被覆にならないものが存在する。このとき $\mathcal{C} \times A$ 上の関係 $R$ を、
\begin{equation*}
R = \{ \, \langle B, y \rangle \in \mathcal{C} \times A \, \mid \, y \notin B \, \}
\end{equation*}
によって定めると、任意有限個の $B_1, B_2, \cdots , B_n \in \mathcal{C}$ に対して $A \setminus (B_1 \cup B_2 \cup \cdots \cup B_n) \neq \emptyset$ だから、
\begin{equation*}
\exists y \in A \, (\langle B_1, y \rangle \in R \land \langle B_2, y \rangle \in R \land \cdots \land \langle B_n, y \rangle \in R)
\end{equation*}
となって $R$ は有限共起的である。従って広大性原理より、
\begin{equation*}
\exists y \in {}^*A \, \forall B \in \mathcal{C} \, (\langle {}^*B, y \rangle \in {}^*R)
\end{equation*}
すなわち
\begin{equation*}
\exists y \in {}^*A \, \forall B \in \mathcal{C} \, (y \notin {}^*B)
\end{equation*}
である。これをみたす $y$ をとると、$y \in \mathrm{monad}(x)$ となる $x \in A$ が存在し、この $x$ に対し $x \in B_0 \in \mathcal{C}$ となる開集合 $B_0$ が存在するから、
\begin{equation*}
y \in \mathrm{monad}(x) \subseteq {}^*B_0
\end{equation*}
すなわち $y \in {}^*B_0$ となるが、一方で $\forall B \in \mathcal{C} \, (y \notin {}^*B)$ より $y \notin {}^*B_0$ だから矛盾である。□
この定理より、コンパクト集合は「超準拡大が各点のモナドで覆い切れる集合」とイメージできます。もっと簡単に言うと「モナドに漏れがない集合」です。この結果も第8回の距離空間に関する結果と整合が取れていることがわかります。
そうすると、ハウスドルフでかつコンパクトな位相空間は「モナドにダブリも漏れもない空間」、どこかで聞いた用語を使うと「モナドがMECEな空間」となります。イメージしやすいですね。
これらの同値条件を使うと、例えば次の定理が論理式を使った簡単な考察だけで証明できます。
【定理6】$A \subseteq X$ とすると、次が成立する。
i) $X$ がコンパクトのとき、$A$ が閉集合ならばコンパクトである。
ii) $X$ がハウスドルフのとき、$A$ がコンパクトならば閉集合である。
i) $X$ がコンパクトのとき、$A$ が閉集合ならばコンパクトである。
ii) $X$ がハウスドルフのとき、$A$ がコンパクトならば閉集合である。
(証明)
i) 任意に $y \in {}^*A$ をとる。$X$ がコンパクトだから【定理5】より $y \in \mathrm{monad}(x)$ となる $x \in X$ が存在する。$y \in \mathrm{monad}(x) \cap {}^*A$ すなわち $\mathrm{monad}(x) \cap {}^*A \neq \emptyset$ で、$A$ は閉集合だから、【定理3】ii) より $x \in A$ となる。従って $\forall y \in {}^*A \, \exists x \in A \, (y \in \mathrm{monad}(x))$ であるから、再び【定理5】より $A$ はコンパクトである。
ii) 任意に $\mathrm{monad}(x) \cap {}^*A \neq \emptyset$ をみたす $x \in X$ をとる。$y \in \mathrm{monad}(x) \cap {}^*A$ をとると、$A$ がコンパクトだから【定理5】より $y \in \mathrm{monad}(x')$ となる $x' \in A$ がある。$\mathrm{monad}(x) \cap \mathrm{monad}(x') \neq \emptyset$ で $X$ がハウスドルフだから、【定理4】ii) より $x = x'$ であり、これより $x \in A$ となる。従って【定理3】ii) より $A$ は閉集合である。
□
なお、$\exists x \in X \, (y \in \mathrm{monad}(x))$ をみたす $y \in {}^*X$ を ${}^*X$ の近標準点といい、そうでない $y \in {}^*X$ を ${}^*X$ の遠標準点といいます。この用語を使うと、空間 $X$ 自身がコンパクトであることは「すべての ${}^*X$ の点が近標準点である」ことと同値です。
[参考文献]
中村 徹『超準解析と物理学(増補改訂版)』(日本評論社, 2017)
(続く)(前記事)(目次)
前の10件 | -



